【从零开始】转起来的螺旋矩阵

这次来看一个二维数组非常经典的两道题目：螺旋矩阵。

对于掌握二维数组的遍历有着极大的帮助。

螺旋矩阵1

leetcode 54 螺旋矩阵

这道题目要求对一个m行n列的矩阵进行一个螺旋式的遍历。

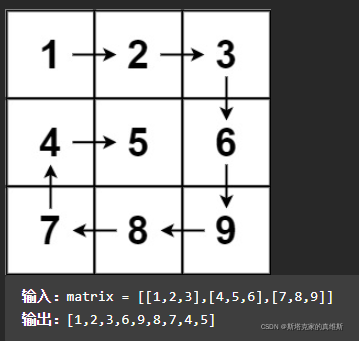
要注意是m行n列的，不是nxn，所以长宽可能不一样。

核心

对于这种数组的遍历，我们先要有一个思维模式。

1. 如何遍历
2. startx与starty对应谁
3. 怎么判断到中间部分了
   
   

遍历

遍历时把拐角留给下一次遍历，遍历过程如下图：

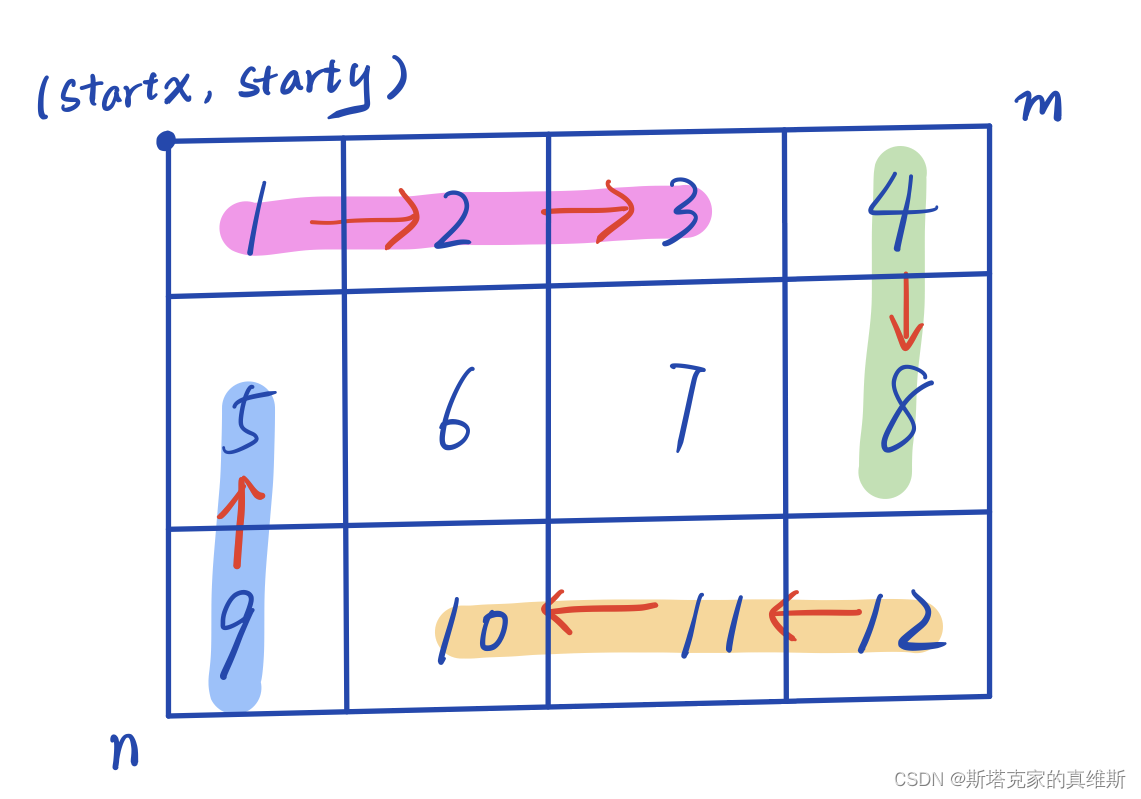
对应关系

startx和starty从起点开始，startx对应的是n，而starty对应的是m。

（这一点如果理解了就很简单，不理解需要举例子，比如（3，2），看看到这个数是如何移动的。）

如何判断循环结束

我们设想一下循环结束时的场景，无非就是像上图中中间还有一列没遍历，又或者是还有一行没遍历。（单独一个也有可能）

而到达上述情况时，要么就是startxn，要么就是startym。

所以边界问题就解决了。

整体

二维数组的遍历其实没有非常复杂，主要是一些条件的处理。

 vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int>res;
        int startx=0;
        int starty=0;

        int n=matrix.size()-1;
        int m=matrix[0].size()-1;

        while(starty<m&&startx<n){
            int i=startx;
            int j=starty;

            for(j=starty;j<m;j++){//循环上边
                res.push_back(matrix[startx][j]);
            }

            for(i=startx;i<n;i++){//循环右边
                res.push_back(matrix[i][j]);
            }

            for(j=m;j>starty;j--){//循环下边
                res.push_back(matrix[i][j]);
            }

            for(i=n;i>startx;i--){//循环左边
                res.push_back(matrix[i][j]);
            }

            //收缩进入下一个圈
            startx++;
            starty++;

            n--;
            m--;

        }

        if(starty==m){
            for(int i=startx;i<=n;i++){
                res.push_back(matrix[i][starty]);
            }
        }
        else if(startx==n){
            for(int j=starty;j<=m;j++){
                res.push_back(matrix[startx][j]);
            }
        }

        return res;

    }

我们在循环时，是要保留拐角的，所以for循环的条件都是<或者>。

收缩边界时，start部分要+1，n和m部分也要-1。

而最终循环结束补齐时，需要<=才可以把剩余的数全部放进来。

螺旋矩阵2

leetcode 59 螺旋矩阵2

这道题和上题其实大同小异。只是规定了nxn的矩阵，需要自己填充数字。

我们完全可以按照上面的遍历逻辑来执行，需要多加一个count变量来给矩阵赋值。

vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> matrix(n, vector<int>(n, 0));
        int startx=0;
        int starty=0;

        int m=n-1;

        int count=1;

        while(startx<m&&starty<m){
            int i=startx;
            int j=starty;

            for(j=starty;j<m;j++){
                matrix[startx][j]=count++;
            }

            for(i=startx;i<m;i++){
                matrix[i][j]=count++;
            }

            for(j=m;j>starty;j--){
                matrix[i][j]=count++;
            }

            for(i=m;i>startx;i--){
                matrix[i][j]=count++;
            }

            startx++;
            starty++;

            m--;
        }
        if(n%2){//判断中心部分
            matrix[n/2][n/2]=count++;
        }
    return matrix;

    }

可以看到前面的步骤都是一致的，让count等于1，然后每次+1就可以循环赋值了。

最后的if判断：

因为对于nxn的矩阵来说，如果n是偶数，那么就多循环一次即可。如果n是奇数，中间会多一个空位出来，也需要赋值。

最后这个if条件可以将空位补齐。