【从零开始的刷题之旅】二叉搜索树（01）：增删改查

二叉搜索树

二叉搜索树是在二叉树的基础上做了一些有序性的处理。

简单来说就是左子树的所有节点值都小于它的根节点，而右子树的所有节点值都大于它的根节点。

因为这个特性，二叉搜索树有一条非常好用的性质：

中序遍历的结果是有序的，并且是升序。

根据这条性质我们可以解决很多问题。

首先是二叉搜索树的增删改查。

二叉搜索树的增删改查

掌握二叉搜索树的这几种基本操作，就可以解决一系列相关问题。

二叉搜索树的搜索

leetcode 700 二叉搜索树中的搜索

给定值，在二叉搜索树中搜索，返回以该值为根的子树。

我们可以用递归来解决，但是比单纯的递归更好的办法是要结合二叉搜索树的左小右大的特性。

在当前节点值小于给定值时，搜索右子树；当前节点值大于给定值时，搜索左子树。

TreeNode* searchBST(TreeNode* root, int val) {
        if(root==NULL)
            return NULL;
        
        if(root->val==val)
        	return root;
        
        if(root->val<val)
            return searchBST(root->right,val);
        if(root->val>val)
            return searchBST(root->left,val);
        
        return NULL;

    }

这样可以提高递归的效率。

二叉搜索树的插入

leetcode 701 二叉搜索树中的插入操作

给定二叉搜索树，插入一个节点再返回。

因为要保证其“左小右大”的特性，所以在插入时需要找到正确的插入位置。

因为二叉搜索树不存在重复的元素，所以我们在插入时按照所有元素独一无二来处理。

如果插入值小于当前节点值，就递归左子树

如果插入值大于当前节点值，就递归右子树

然后在遇到NULL时就可以插入了。

TreeNode* insertIntoBST(TreeNode* root, int val) {
        
        if(root->val>val){
            root->left=insertIntoBST(root->left,val);
        }

        if(root->val<val){
            root->right=insertIntoBST(root->right,val);
        }
        
        if(root==NULL){
            TreeNode* newNode=new TreeNode(val);
            return newNode;
        }
        return root;

    }

插入操作就是在空节点的基础上新建一个节点，然后递归返回即可。

二叉搜索树的删除

插入节点比较直接，而删除节点就没有这么简单了。

因为插入节点会在叶子节点处，而删除节点有可能在叶子，有可能不在，需要考虑多种情况。

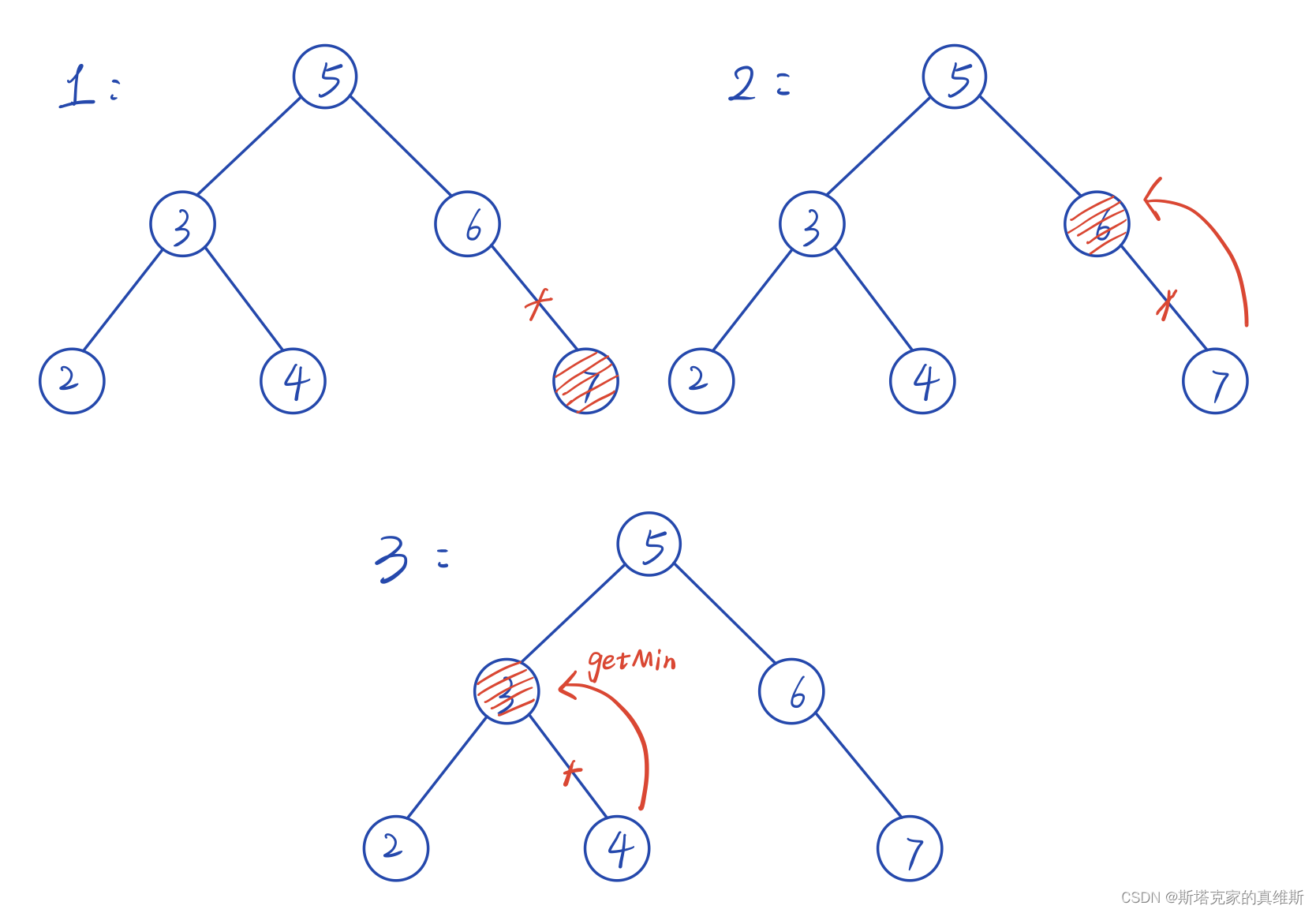
大致分为以上三种情况：

1.删除的是叶子节点，那么直接返回NULL就可以了。

2.删除的不是叶子节点，但左子树或者右子树不存在，那么直接用子树节点代替即可

3.删除的节点左子树和右子树都存在，这个时候要返回右子树中最小的节点，来替换掉被删除的节点，同时还要

当然，在删除之前还是要按照搜索的模式去找到这个节点的。

TreeNode* deleteNode(TreeNode* root, int key) {
        //先找到才能删
        if(root==NULL)
            return NULL;
        if(root->val==key){
            ...

            }

        else if(root->val<key){
            root->right=deleteNode(root->right,key);

        }
        else if(root->val>key){
            root->left=deleteNode(root->left,key);

        }
        return root;


    }

然后对应每种情况，我们再来写root->val==key的具体判断

//是叶子节点，直接删
if(root->left==NULL&&root->right==NULL)
         return NULL;
//左子树为空，用右子树代替
if(root->left==NULL&&root->right!=NULL)
         return root->right;
//右子树为空，用左子树代替
if(root->right==NULL&&root->left!=NULL)
         return root->left;

//最复杂的情况 左右子树都有
if(root->left!=NULL&&root->right!=NULL){
    TreeNode* minNode=getMin(root->right);//用getMin函数找到右边最小的值
                
    root->right=deleteNode(root->right,minNode->val);//把这个节点记录下来后删掉
    //与要删的节点做交换
    minNode->left=root->left;
    minNode->right=root->right;
    root=minNode;

当然交换节点时修改val值也可以通过，但是不够严谨。

再来说一下getMin函数的实现：

因为是要找右子树的最小值，根据二叉搜索树的特性，一定是在最左边，所以不断搜索左子树即可。

TreeNode* getMin(TreeNode* root){
        while(root->left){
            root=root->left;
        }
        return root;
    }

这样删除操作就搞定了

TreeNode* getMin(TreeNode* root){
        while(root->left){
            root=root->left;
        }
        return root;
    }
    
TreeNode* deleteNode(TreeNode* root, int key) {
        //先找到才能删
        if(root==NULL)
            return NULL;
        if(root->val==key){
            if(root->left==NULL&&root->right==NULL)
                return NULL;
            if(root->left==NULL&&root->right!=NULL)
                return root->right;
            if(root->right==NULL&&root->left!=NULL)
                return root->left;

            //最复杂的情况
            if(root->left!=NULL&&root->right!=NULL){
                TreeNode* minNode=getMin(root->right);
                
                root->right=deleteNode(root->right,minNode->val);
                minNode->left=root->left;
                minNode->right=root->right;
                root=minNode;

            }

        }

        else if(root->val<key){
            root->right=deleteNode(root->right,key);

        }
        else if(root->val>key){
            root->left=deleteNode(root->left,key);

        }
        return root;


    }

验证二叉搜索树

验证一棵二叉树是不是二叉搜索树，看上去很简单，但是也有一些坑在里面。

二叉搜索树的性质是所有左子树的值都小于根节点，右子树都大于根节点。

但这条性质不能直接用递归反过来判断是否是二叉搜索树。

因为我们在递归时只判断了当前树的左子树和右子树是否符合，但无法判断对根节点是否一样适用。

也就是这样的情况：

比较直接的想法是利用中序遍历有序的性质，将节点值放入vector，然后判断数组是否是升序的。

这里我们再用另一种方法解决，不需要额外的空间。

用一个指针指向前一个节点的值，在中序遍历时对比它和当前值的大小，如果一直是升序的那么就说明符合二叉搜索树的要求。

TreeNode* node=NULL;
    bool isValidBST(TreeNode* root) {
        if(root==NULL)
            return true;
        bool left=isValidBST(root->left);
        if(node!=NULL&&node->val>=root->val)
            return false;
        
        node=root;

        bool right=isValidBST(root->right);
        return left&&right;


    }