【深度学习】空洞卷积（扩张卷积）和一般卷积的区别 Dilated Convolution

---

前言

目前来说有一个想法，距离寒假还有一个月，想在放寒假之前把深度学习这半年来的基础知识都补充回归一下，以写成博客的形式进行汇总。
今天回顾的主要是理论方面的——空洞卷积。

一、感受野

感受野定义：输出的特征图中每一个元素所对应的输入层区域的大小
因为我们知道，卷积具有浓缩的作用，原本一个较大的输入尺寸，经过卷积之后会变成一个较之前小一点的尺寸，这就是卷积起到了浓缩的作用。
我们做两个实验看看就知道了：

import torch
import torch.nn as nn
x1=torch.rand(1,5,5)
conv=nn.Conv2d(1,1,3,1,0)
y1=conv(x1)
print(y1.shape)

x2=torch.rand(1,3,3)
conv=nn.Conv2d(1,1,3,1,0)
y2=conv(x2)
print(y2.shape)

实验结果如下：

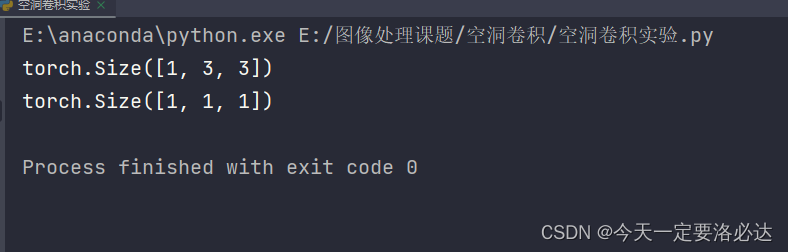
第一个输入的是一维的5×5的尺寸大小，经过最简单的310卷积后，变成了一维的3×3尺寸。这里3×3卷积每一个元素对应5×5中3个元素，感受野是3×3（相当于是卷积核的大小）。

第二个输入的是一维的3×3的尺寸大小，经过最简单的310卷积后，变成了一维的1×1尺寸。这里1×1卷积每一个元素（也就一个元素）对应3×3中3个元素（所有的元素），感受野是3×3（相当于是卷积核的大小）。

从这里我们也能看出，5×5的卷积 ，经过两次3×3卷积，就能变成一个元素（1×1）

二、空洞卷积

空洞卷积是啥：也就是在普通卷积里加入空洞（0）：
空洞卷积相比于普通卷积，多了一个超参数：膨胀率（dilation）
（补充概念：超参数 比如卷积的超参数有卷积核大小，步长等等）
在一般情况下，nn.conv2D里的dilation设置默认为1

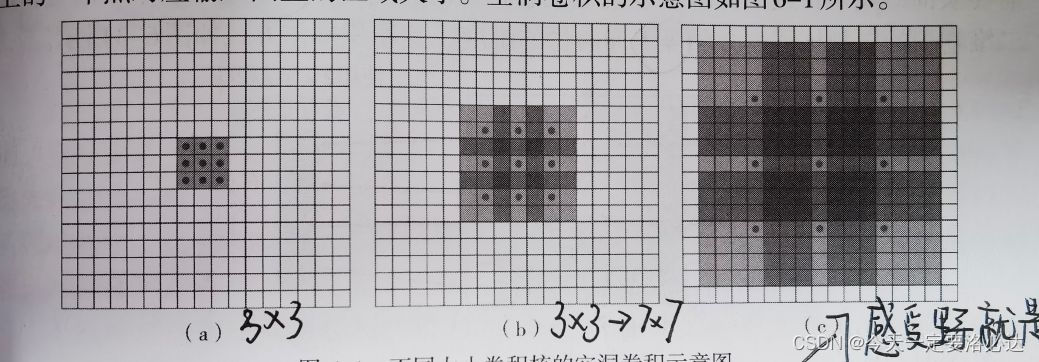
图a是3X3的1-空洞卷积，感受野与普通3X3一致，也就是此时dilation默认为1
图b是7X7的2-空洞卷积，感受野与普通7X7一致，也就是此时dilation为2
图c是15X15的4-空洞卷积，感受野与普通15X15一致，也就是此时dilation为4
（当然这部分和下面实验的结果有部分冲突）
我们做实验看看：

import torch
import torch.nn as nn
x1=torch.rand(1,5,5)
conv=nn.Conv2d(1,1,3,1,0,dilation=2)
y1=conv(x1)
print(y1.shape)

x2=torch.rand(1,9,9)
conv=nn.Conv2d(1,1,3,1,0,dilation=4)
y2=conv(x2)
print(y2.shape)

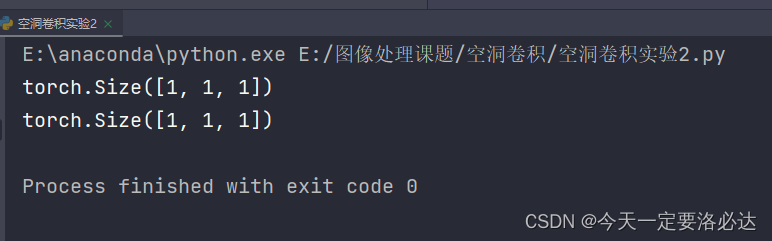
3X3，膨胀率为2的卷积，感受野为5X5
3X3，膨胀率为4的卷积，感受野为9X9（确实和上面的有区别）
从这里我们也能看出，空洞卷积那9个参数构成矩阵外面的0好像没起作用？

空洞卷积的优势：
最开始在图像分割领域被提出来的，用来增加感受野。（感受野不仅增加了，而且也是9个参数）

利用空洞卷积，感受野呈指数级增长：？
以3X3为例：
普通卷积：1——3——5——7——9…(增长目测为线性)
空洞卷积：1——3——7——15 （依次通过膨胀率=1，2，4的卷积核）

三.补充：padding

用了这么久的padding，padding到底有啥用呢，如何更细致理解一下？：
最大的一个作用我觉得应该是：提高边界元素的利用性，正常卷积下边界的像素值只会被卷一次，这会大大降低边界元素的重要性。padding之后，就能多卷几次。