置换检验及其matlab代码

目录

一、基本概念

二、实例

---

参考链接：https://www.iikx.com/news/statistics/1824.html

https://www.zhihu.com/question/26629875/answer/392615941

一、基本概念

Permutation test 置换检验是Fisher于20世纪30年代提出的一种基于大量计算（computationally intensive），利用样本数据的全（或随机）排列，进行统计推断的方法，因其对总体分布自由，应用较为广泛，特别适用于总体分布未知的小样本资料，以及某些难以用常规方法分析的假设检验问题。在具体使用上它和Bootstrap Methods类似，通过对样本进行顺序上的置换，重新计算统计检验量，构造经验分布，然后在此基础上求出P-value进行推断。

置换检验中一个重要的前提假设时观察样本在原假设下是可交换的。

在比较均值和零的单样本检验中，样本间的置换相当于随意改变样本的符号。

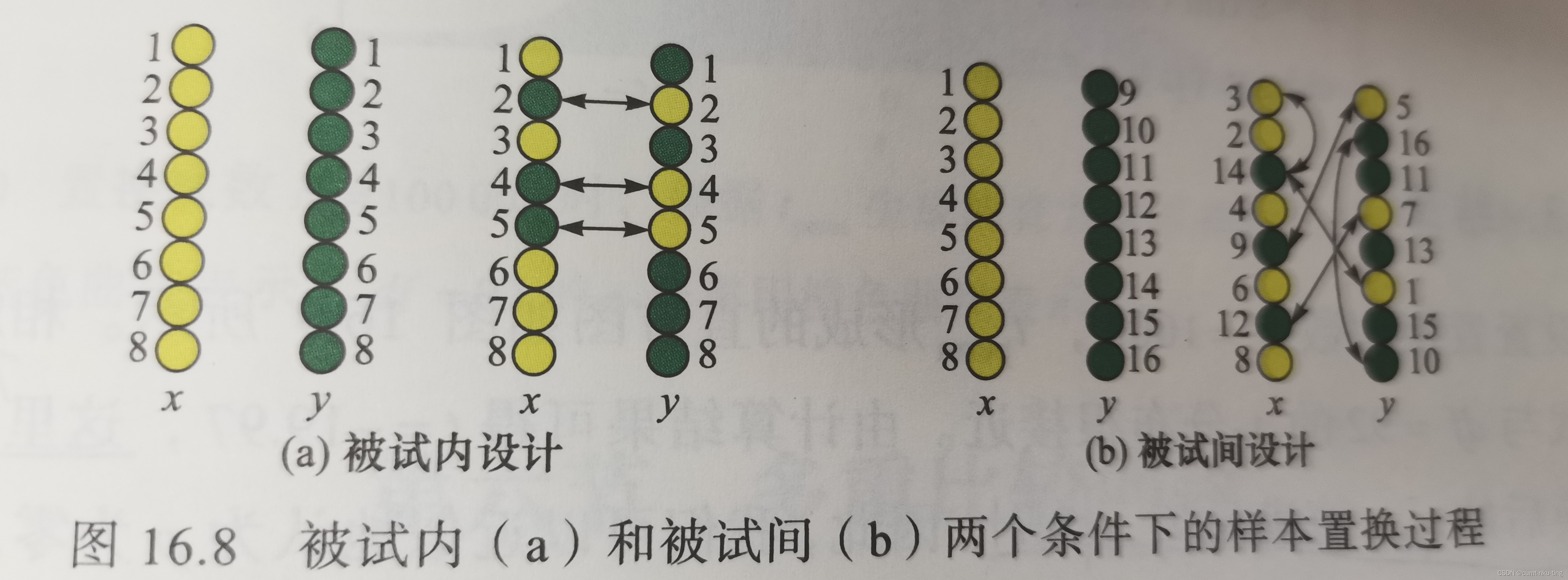
如果比较两个或多个条件下的平均值，则样本间的置换相当于随机改变每个样本的实验条件的标签。在进行被试内检验时，不同条件下的样本来自同一组被试，交换每名被试内的条件标签而不是被试之间的条件标签来进行样本置换；在进行被试间检验时，不同条件下的样本来自不同组的被试，通过交换被试之间的条件标签来进行样本的置换。

二、实例

H0：静息态脑电信号功率在睁眼和闭眼条件下的差值的均值是0；

H1：静息态脑电信号功率在睁眼和闭眼条件下的差值的均值不是0；

clc;clear;close all;                        
[num,txt,raw] = xlsread('Resting State.xlsx');      
x=num(:,3);                             
n=size(x,1);                            
tval=mean(x)./(std(x)/sqrt(n));             
                                    
%% permutation                          
N=1000;                                
y=x*ones(1,N).*((randn(n,N)>0)*2-1);            
t_permute = mean(y,1)./(std(y,1)/sqrt(n));      
p=sum(abs(tval)<abs(t_permute))/N;              
disp(p);
 
 
fig=figure();
hold on;grid on; box on;
histogram(t_permute,100,'Normalization','pdf');
[f,xi] = ksdensity(t_permute);
plot(xi,f,'linewidth',3);
xlim([-4,4])
xlabel('t');
set(gca,'fontsize',18)

置换次数N=1000； p=0

 这里不存在任何置换后的值满足，因此，可以近似的认为p等于0，因此拒绝原假设H0，接受备择假设H1.

但是N=1000，求取p时最小间隔为0.001，其落在p=0.05附近的不确定性约为1%。

置换次数N=1000； p=0

N=100 000，求取p时最小间隔为0.00 001，其落在p=0.05附近的不确定性约为0.01%。其概率密度分布函数更接近df=92的t-分布。