1230k倍区间，关于cnt[0]赋值为1的解释

题目描述

给定一个长度为 N 的数列，A1,A2,…AN，如果其中一段连续的子序列 Ai,Ai+1,…Aj 之和是 K 的倍数，我们就称这个区间 [i,j] 是 K 倍区间。

你能求出数列中总共有多少个 K 倍区间吗？

输入格式
第一行包含两个整数 N 和 K。

以下 N 行每行包含一个整数 Ai。

输出格式
输出一个整数，代表 K 倍区间的数目。

数据范围
1≤N,K≤100000,
1≤Ai≤100000

样例

5 2
1
2
3
4
5

输出
6

关于cnt[0]赋值为1的解释

	在处理cnt[a[i]%k] == 0 的情况，因为mod k ==0 此时他自身就是一个k倍区间,但
我们在程序中，是按照两个一组来进行配对的，所以需要重新考虑。
	将cnt[0]赋值为1的初始化，因为res每次需要加cnt[0]，与每一个元素进行组合，
这样每次res+cnt[0]就会多加一个1，这个1可以视为这一次循环中，新的符合a[i]%k==0
的一个前缀和。这样就可以补充它本身是一个k倍区间的情况了。

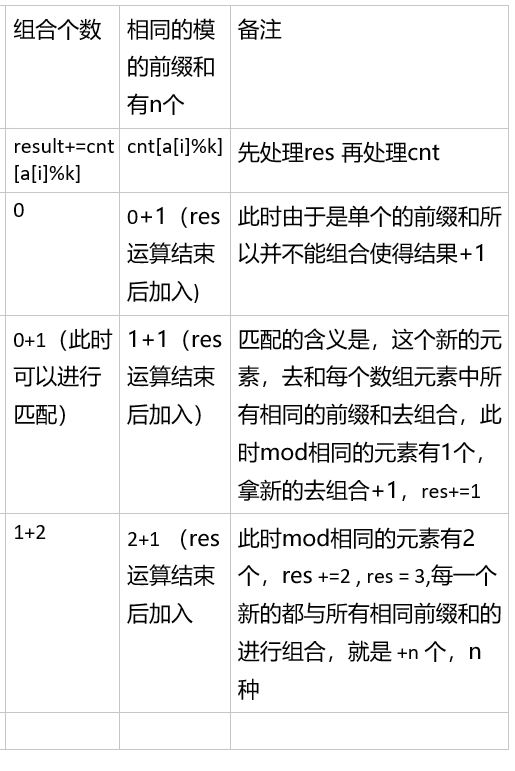
做法解析

	前提：数组为前缀和
	cnt[i]可以视为取余结果为i的区间 的个数
	根据题意得到:(a1-b1)%k==0
变形：a1%k-b1%k==0 a1%k == b1%k
所以只要任意两个前缀和 mod的值相等就可以了
对于其他的取余结果为非0的结果来说需要两个区间才能组合。

C++ 代码

//k倍区间

#include<bits/stdc++.h>

using namespace std;

const int N = 100010;

long long a[N], cnt[N];

long long res = 0;
int n, k;

int main(void){
    cin >> n >> k;
    for(int i=1; i<=n; i++){
        cin >> a[i];
        a[i] += a[i-1];
    }

    cnt[0] = 1;

    for(int i=1; i<=n; i++){

        res += cnt[a[i]%k];
        cnt[a[i]%k] ++ ;
    }

    cout<< res;
    system("pause");
}