2025高维多目标优化：基于导航变量的多目标螳螂搜索算法（Multi-objective Mantis Search Algorithm ，MOMSA）求解无人机三维路径规划，MATLAB代码

本文链接：https://blog.youkuaiyun.com/weixin_46204734/article/details/146155826

一、多目标螳螂搜索算法MOMSA

多目标螳螂搜索算法（Multi-objective Mantis Search Algorithm ，MOMSA）由Mohammed Jameel和Mohamed Abouhawwash于2024年提出，其灵感来自于螳螂独特的狩猎行为和性同类相食行为。所提出的 MOMSA 算法采用相同的底层 MSA 收敛机制，并结合精英非支配排序方法来估计帕累托最优解。此外，MOMSA采用拥挤距离机制来增强最优解对所有目标的覆盖范围。

参考文献：

[1]Mohammed Jameel, Mohamed Abouhawwash,Multi-objective Mantis Search Algorithm (MOMSA): A novel approach for engineering design problems and validation,Computer Methods in Applied Mechanics and Engineering,Volume 422,2024,116840,ISSN 0045-7825,https://doi.org/10.1016/j.cma.2024.116840.

原文链接：https://blog.youkuaiyun.com/weixin_46204734/article/details/136581045

二. 无人机路径规划问题描述

2.1 运动学模型和约束

无人机在三维空间中的运动学模型可以用以下方程描述：

$\begin{cases} \dot{x} = V \cos \alpha \cos \beta \ \dot{y} = V \cos \alpha \sin \beta \ \dot{z} = V \sin \alpha \end{cases}$

其中：

$x, y, z$ 表示无人机在三维空间中的位置坐标。
$V$ 表示无人机的线速度。
$\alpha$ 表示爬升角。
$\beta$ 表示转向角。

无人机的运动学约束条件如下：

$\begin{cases} V_{\min} \leq V \leq V_{\max} \ |\Delta \alpha| = |\theta| \leq \theta_{\max} \ |\Delta \beta| = |\psi| \leq \psi_{\max} \end{cases}$

其中：

$V_{\min}$ 和 $V_{\max}$ 分别表示无人机的最小和最大线速度。
$\theta_{\max}$ 和 $\psi_{\max}$ 分别表示无人机的最大爬升角和最大转向角。
$\theta$ 和 $\psi$ 分别表示无人机的爬升角和转向角的变化量。

这些约束条件确保无人机在飞行过程中不会超出其物理能力范围，从而保证飞行的安全性和可行性。

2.2 路径规划的目标函数

无人机路径规划问题可以描述为在三维空间中找到一条从起点到终点的路径，该路径需要满足以下要求：

路径长度最短：减少飞行时间和能量消耗。
避免障碍物：确保飞行安全。
飞行高度稳定：减少能量消耗并提高飞行稳定性。
路径平滑：减少转向角度的变化，降低能量消耗。

这些要求可以通过以下四个目标函数来量化：

2.2.1 路径长度 (F1)

路径长度的目标函数 $F_1$ 用于衡量路径的总长度。路径长度越短，无人机的飞行效率越高。目标函数 $F_1$ 定义为：

$F_1 = \begin{cases} 1 - \frac{\| \overrightarrow{P_{i1}P_{in}} \|}{\sum_{j=1}^{n-1} \| \overrightarrow{P_{ij}P_{i,j+1}} \|}, & \text{if } \| \overrightarrow{P_{ij}P_{i,j+1}} \| \geq R_{\min} \\ \infty, & \text{otherwise} \end{cases}$

其中：

$R_{\min}$ 是两个航点之间的最小距离。
$\| \overrightarrow{P_{ij}P_{i,j+1}} \|$ 表示两个连续航点之间的欧几里得距离。

2.2.2 避碰 (F2)

避碰的目标函数 $F_2$ 用于确保无人机在飞行过程中避免与障碍物碰撞。目标函数 $F_2$ 定义为：

$F_2 = \frac{1}{K(n-1)} \sum_{j=1}^{n-1} \sum_{k=1}^{K} T_k(\overrightarrow{P_{ij}P_{i,j+1}})$

其中：

$K$ 是工作区域中的障碍物数量。
$T_k$ 计算如下：
$T_k(\overrightarrow{P_{ij}P_{i,j+1}}) = \begin{cases} 0, & \text{if } d_k \geq D + R_k + S \\ 1 - \frac{d_k - D - R_k}{S}, & \text{if } D + R_k < d_k < D + R_k + S \\ \infty, & \text{otherwise} \end{cases}$
$d_k$ 是障碍物 $k$ 的中心到路径段 $P_{ij}P_{i,j+1}$ 的距离。
$D$ 是无人机的尺寸。
$R_k$ 是障碍物 $k$ 的半径。
$S$ 是无人机与障碍物之间的安全距离。

2.2.3 飞行高度 (F3)

飞行高度的目标函数 $F_3$ 用于确保无人机在飞行过程中保持稳定的飞行高度，以减少能量消耗。目标函数 $F_3$ 定义为：

$F_3 = \frac{1}{n} \sum_{j=1}^{n} H_{ij}$

其中：
$H_{ij} = \begin{cases} \frac{2|h_{ij} - h_{\text{mean}}|}{h_{\max} - h_{\min}}, & \text{if } h_{\min} \leq h_{ij} \leq h_{\max} \\ \infty, & \text{otherwise} \end{cases}$

$h_{\max}$ 和 $h_{\min}$ 分别是最大和最小相对飞行高度。
$h_{\text{mean}} = \frac{h_{\max} + h_{\min}}{2}$ 是优选的相对飞行高度。
$h_{ij}$ 是无人机在航点 $P_{ij}$ 处的高度。

2.2.4 平滑度 (F4)

平滑度的目标函数 $F_4$ 用于衡量无人机飞行路径的平滑程度，以减少转向角度的变化，从而降低能量消耗。目标函数 $F_4$ 定义为：

$F_4 = \frac{1}{n-2} \sum_{j=1}^{n-2} \frac{|\eta_{ij}|}{\pi}$

其中：
$\eta_{ij} = \arctan \left( \frac{\| \overrightarrow{P_{ij}P_{i,j+1}} \times \overrightarrow{P_{i,j+1}P_{i,j+2}} \|}{\overrightarrow{P_{ij}P_{i,j+1}} \cdot \overrightarrow{P_{i,j+1}P_{i,j+2}}} \right)$

$\eta_{ij}$ 是两个连续路径段之间的转向角。

三. 多目标优化方法求解无人机路径规划介绍

3.1. 导航变量表示

多目标优化算法采用导航变量来表示无人机的路径，每个路径段由三个参数描述：

路径段长度（ $r$ ）：表示两个连续航点之间的距离。
爬升角（ $\theta$ ）：表示无人机在垂直方向上的角度变化。
转向角（ $\psi$ ）：表示无人机在水平方向上的角度变化。

通过导航变量，可以将无人机的路径表示为一系列有序的航点，每个航点由导航变量确定其在三维空间中的位置。

由于上述目标函数之间可能存在冲突，因此采用多目标优化方法来寻找帕累托最优解。

3.2 帕累托最优解

帕累托最优解的定义如下：

一个解 $X$ 是非支配的，如果不存在其他解 $X^{'}$ 使得 $F_i(X') \leq F_i(X)$ 对所有 $i$ 成立，并且至少有一个 $j$ 使得 $F_j(X') < F_j(X)$ 。
一个解 $X^*$ 是帕累托最优的，如果它是非支配的。
帕累托最优集 $P^*$ 是所有非支配解的集合。

3.3 导航变量的多目标优化算法求解

路径长度（ $F_1$ ）：最小化路径总长度，以减少飞行时间和能量消耗。
避碰（ $F_2$ ）：确保无人机在飞行过程中避免与障碍物碰撞。
飞行高度（ $F_3$ ）：维持稳定的飞行高度，以减少能量消耗并提高飞行稳定性。
路径平滑度（ $F_4$ ）：最小化路径中的转向角度变化，以降低能量消耗。

3.4 输出结果

生成帕累托最优路径：从非支配解集中提取所有路径，作为帕累托最优解。
路径后处理：根据应用需求，对帕累托最优路径进行进一步筛选和优化，生成最终的飞行路径。

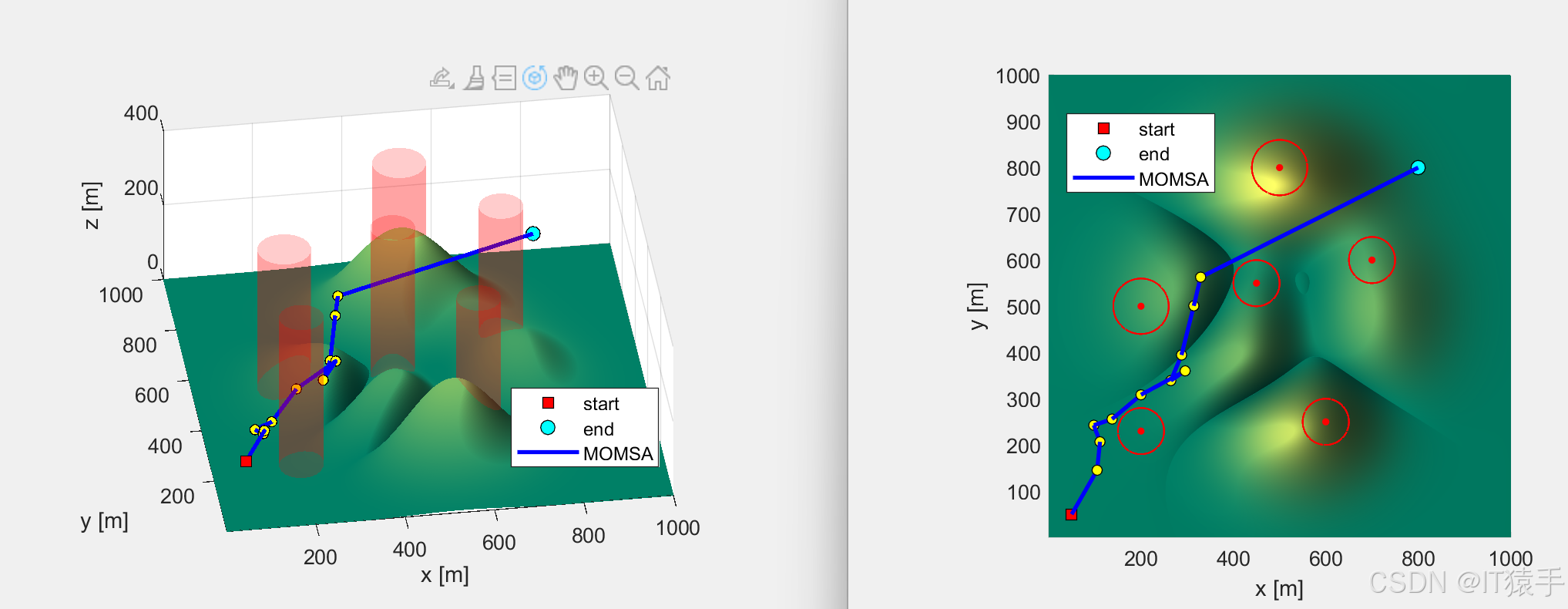
四、部分代码及部分结果

%% Problem Definition
model = CreateModel(); % Create search map and parameters
model_name = 6;

nVar=model.n;       % Number of Decision Variables = searching dimension of PSO = number of path nodes

VarSize=[1 nVar];   % Size of Decision Variables Matrix

% Lower and upper Bounds of particles (Variables)
VarMin.x=model.xmin;           
VarMax.x=model.xmax;           
VarMin.y=model.ymin;           
VarMax.y=model.ymax;           
VarMin.z=model.zmin;           
VarMax.z=model.zmax;                 

VarMax.r=3*norm(model.start-model.end)/nVar;  % r is distance
VarMin.r=VarMax.r/9;

% Inclination (elevation)
AngleRange = pi/4; % Limit the angle range for better solutions
VarMin.psi=-AngleRange;            
VarMax.psi=AngleRange;          

% Azimuth 
VarMin.phi=-AngleRange;            
VarMax.phi=AngleRange;          

% Lower and upper Bounds of 
alpha=0.5;
VelMax.r=alpha*(VarMax.r-VarMin.r);    
VelMin.r=-VelMax.r;                    
VelMax.psi=alpha*(VarMax.psi-VarMin.psi);    
VelMin.psi=-VelMax.psi;                    
VelMax.phi=alpha*(VarMax.phi-VarMin.phi);    
VelMin.phi=-VelMax.phi;