数据结构与算法 排序

一.概述
1.基于比较的排序:

以下排序都是"基于比较的排序"(Comparison-Based Sorting),即除赋值外,对输入的数据进行的操作只能是大于/小于的比较(>/<)
另外,将假定传入到排序函数中的数据都是合法的,并用1个数组接收;同时接收1个int,表示共传入几个数据
最后,注意位置都是从0开始的.所以在位置i处的数据实际上是第i+1个数据

2.简单排序算法的下界:

假设序列中不存在重复元素且所有排列都是等可能的.在这些假设下,有如下定理:

定理7.1:$N$个互异数构成的数组的平均逆序数是$\frac{N(N-1)}{4}$

定理7.2:通过交换相邻元素进行排序的任何算法平均需要$\Omega (N^2)$的时间

二.插入排序
1.基本思想:

"插入排序"(Insertion Sort)通过N-1次插入来实现排序:第i次(1≤i≤N-1)插入将第i+1个的数据插入到前i+1个数据中合适的位置处(见下表)

初始	3 4 1 4 3 1 4 0 11 42	移动的元素
p=1后	3 4 1 4 3 1 4 0 11 42	×
p=2后	1 3 4 4 3 1 4 0 11 42	A[2]
p=3后	1 3 4 4 3 1 4 0 11 42	×
p=4后	1 3 3 4 4 1 4 0 11 42	A[4]
p=5后	1 1 3 3 4 4 4 0 11 42	A[5]
p=6后	0 1 1 3 3 4 4 4 11 42	A[6]
p=7后	0 1 1 3 3 4 4 4 11 42	×
p=8后	0 1 1 3 3 4 4 4 11 42	×

2.代码实现:

#include <stdio.h>
typedef int ElementType;

void InsertionSort(ElementType A[], int N) {
	int j, P;
	ElementType Tmp;
	for (P = 1; P < N; P++) {
		Tmp = A[P];
		for (j = P; j > 0 && A[j - 1] > Tmp; j--) {
			A[j] = A[j - 1];
		}
		A[j] = Tmp;
	}
}

int main() {
	ElementType A[10] = { 3,4,1,4,3,1,4,0,11,42 };
	InsertionSort(A, 10);
	int i;
	for (i = 0; i < 10; i++) {
		printf("%d ", A[i]);
	}
}
//结果:
0 1 1 3 3 4 4 4 11 42

3.算法分析:

最坏和平均时间复杂度均为O(N^2),最好时间复杂度(要求输入的A是已排序的)为O(N).空间复杂度为O(1)

三.希尔排序
1.基本思想:

"希尔排序"(Shell Sort)通过比较相隔一定距离的元素来工作,且每轮排序中比较的距离随着算法的进行而缩小,直到只比较相邻元素的最后1轮为
止,因此希尔排序也叫"缩小增量排序"(Diminishing Increment Sort)
希尔排序使用1个"增量序列"(Increment Sequence)h1,h2...ht来确定每轮比较的距离.理论上,只要满足h1=1,任何增量序列都是可行的,不过
有些更好.使用增量hk的1轮排序后,对∀i有A[i]≤A[i+hk],此时称序列是"hk-排序的"(hk-sorted)(见下表).并且希尔排序的1个重要性质是1个
hk-排序的序列将保持其hk-排序性.事实上,如果并非如此,该算法也就没有什么意义了,因为各次排序的结果会被之后的各次排序打乱

初始	81 94 11 96 12 35 17 95 28 58 41 75 15
在5-排序后	35 17 11 28 12 41 75 15 96 58 81 94 95
在3-排序后	28 12 11 35 15 41 58 17 94 75 81 96 95
在1-排序后	11 12 15 17 28 35 41 58 75 81 94 95 96

hk-排序的一般做法是:对hk,hk+1...N-1中的每个位置i,把其上的元素放到i,i-hk,i-2*hk...中的正确位置上.也就是说,1轮hk-排序的作用就
是对hk个独立的子数组执行1次插入排序

2.代码实现:

#include <stdio.h>
typedef int ElementType;

void ShellSort(ElementType A[], int N) {
	int i, j, Increment;
	ElementType Tmp;
	for (Increment = N / 2; Increment > 0; Increment /= 2) {//这里使用的是希尔增量序列
		for (i = Increment; i < N; i++) {
			Tmp = A[i];
			for (j = i; j >= Increment; j -= Increment) {
				if (Tmp < A[j - Increment]) {
					A[j] = A[j - Increment];
				}
				else {
					break;
				}
			}
			A[j] = Tmp;
		}
	}
}

int main() {
	ElementType A[10] = { 3,4,1,4,3,1,4,0,11,42 };
	ShellSort(A, 10);
	int i;
	for (i = 0; i < 10; i++) {
		printf("%d ", A[i]);
	}
}
//结果:
0 1 1 3 3 4 4 4 11 42

3.算法分析:

希尔排序的运行时间依赖于增量序列的选择.下面证明在2个特定增量序列下最坏情况的精确边界

增量序列的1种流行(但不好)的选择是使用Shell建议的增量序列:$$h_t=\lfloor \frac{N}{2}\rfloor ,h_k=\lfloor \frac{h_{k+1}}{2}\rfloor$$
定理7.3:使用希尔增量序列时希尔排序的最坏情形运行时间为$\Theta (N^2)$

Hibbard提出了另1个更好的增量序列:$$1,3,7...2^k-1$$定理7.4:使用Hibbard增量序列的希尔排序的最坏情形运行时间为$\Theta (N^{\frac{3}{2}})$

其他增量序列:

四.堆排序
1.基本思想:

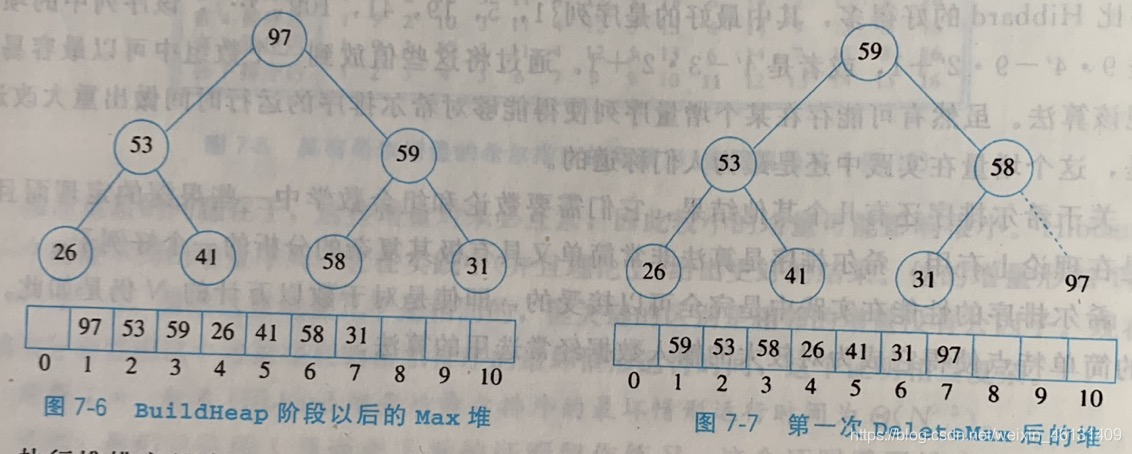
"堆排序"(Heapsort)使用优先队列进行排序:首先建立1个包含所有要排序的元素的二叉堆,花费O(N)的时间;然后执行N次DeleteMaxPriority(),并
用1个数组按顺序接收被删除的元素,每次花费O(log N)的时间;再将数组拷贝回原数组,花费O(N)的时间.这样就得到了这N个元素从小到大排序后的数
组.每次删除花费O(log N)的时间,因此总的运行时间是O(N*log N)
该算法的问题在于使用了1个额外的数组,因此所需的内存资源增加了1倍.1种解决方法是在每次DeleteMaxPriority()后,让堆缩小1个元素的大小;并
将刚删去的元素放在节约出的空间上.使用此策略时,为了最终得到递增的序列,应使用最大堆

2.实现:

在下述实现中,由于速度的原因没有使用实际的max二叉堆,而是使用了1个数组来模拟二叉堆

#define LeftChild(i) (2*(i)+1)
typedef int ElementType;

void PercDown(ElementType A[],int i,int N) {
    int Child;
    ElementType Tmp;
    for (Tmp = A[i];LeftChild(i) < N;i = Child) {
        Child = LeftChild(i);
        if (Child != N - 1 && A[Child + 1] > A[Child]) {
            Child++;
        }
        if (Tmp < A[Child]) {
            A[i] = A[Child];
        } else {
            break;
        }
    }
    A[i] = Tmp;
}

void Swap(ElementType * a,ElementType * b) {
    ElementType Temp = *a;
    *a = *b;
    *b = Temp;
}

void HeapSort(ElementType A[],int N) {
    int i;
    for (2 = N / 2;i >= 0;i--) {//建立max二叉堆
        PercDown(A,i,N);
    }
    for (i = N - 1;i > 0;i--) {
        Swap(&A[0],&A[i]);//DeleteMaxPriority
        PercDown(A,O,i);
    }
}

3.算法分析:

定理7.5:对$N$个互异项的随机排列进行堆排序,所用的平均比较次数为$2N\log N-O(N\log \log N)$

五.归并排序
1.基本思想:

"归并排序"(Merge Sort)是1种递归算法,也是1种分治算法.其基本操作是合并2个已排序的表.合并算法使用了2个输入数组A,B/1个输出数组C/3个计
数器Aptr,Bptr,Cptr:3个计数器均从各自对应的数组的首元素开始;不断将A[Aptr]和B[Bptr]中的较小者拷贝到C[Cptr];每次拷贝后都将使用到的
2个计数器+1.归并排序的原理为:将全部数据分为2部分,递归地对2部分分别进行归并排序,然后使用上述方法合并这2部分

2.实现:

#include <stdio.h>
#include <malloc.h>
typedef int ElementType;

void Merge(ElementType A[],ElementType TmpArray[],int Lpos,int Rpos,int RightEnd) {
    int i,LeftEnd = Rpos - 1,NumElements = RightEnd - Lpos + 1,TmpPos = Lpos;
    while (Lpos <= LeftEnd && Rpos <= RightEnd) {
        if (A[Lpos] <= A[Rpos]) {
            TmpArray[TmpPos++] = A[Lpos++];
        } else {
            TmpArray[TmpPos++] = A[Rpos++];
        }
    }
    while (Lpos <= LeftEnd) {
        TmpArray[TmpPos++] = A[Lpos++];
    }
    while (Rpos <= RightEnd) {
        TmpArray[TmpPos++] = A[Rpos++];
    }
    for (i = 0;i < NumElements;i++,RightEnd--) {
        A[RightEnd] = TmpArray[RightEnd];
    }
}

void MSort(ElementType A[],ElementType TmpArray[],int Left,int Right) {
    int Center;
    if (Left < Right) {
        Center = (Left + Right) / 2;
        MSort(A,TmpArray,Left,Center);
        MSort(A,TmpArray,Center + 1,Right);
        Merge(A,TmpArray,Left,Center + 1,Right);
    }
}

void MergeSort(ElementType A[],int N) {
    ElementType * TmpArray;
    TmpArray = malloc(N * sizeof(ElementType));
    if (TmpArray != NULL) {
        MSort(A,TmpArray,0,N-1);
        free(TmpArray);
    }
}

int main(void) {
	ElementType A[10] = {3,4,1,9,3,4,2,22,11,7};
	MergeSort(A,10);
	int i;
	for (i = 0;i < 10;i++) {
		printf("%d ",*(A + i));
	}
	return 0;
}
//结果:
1 2 3 3 4 4 7 9 11 22

3.算法分析:

合并2个已排序的表的时间是线性的:因为除最后1次比较外,每次比较后只将1个元素放入$C$而最后1次比较后至少将2个元素放入$C$,因此最多进行N-1次比较,其中N为2个表中的元素总数

假设$N=2^k$,从而可将全部元素分为均包含偶数个元素的2部分.若$N=1$,则用时为常数;否则,用时为完成2个大小为$N/2$的归并排序的用时加合并2个已排序的表的用时.也就是说:$$\begin{gathered} T(1)=1 \\ T(N)=2T(\frac{N}{2})+N \end{gathered}$$
求解该递归关系的方法有多种:
$$\begin{gathered} ①T(N)=2T(\frac{N}{2})+N\Rightarrow \frac{T(N)}{N}=\frac{T(\frac{N}{2})}{\frac{N}{2}}+1 \\ \Rightarrow \{\begin{array}{l}\frac{T(N)}{N}=\frac{T(\frac{N}{2})}{\frac{N}{2}}+1\\ \frac{T(\frac{N}{2})}{\frac{N}{2}}=\frac{T(\frac{N}{4})}{\frac{N}{4}}+1\\ ...\\ \frac{T(2)}{2}=\frac{T(1)}{1}+1\end{array} \\ \Rightarrow \frac{T(N)}{N}=\frac{T(1)}{1}+\log N \\ \Rightarrow T(N)=N\log N+N \\ =O(N\log N) \\ ②\{\begin{array}{l}T(N)=2T(\frac{N}{2})+N\\ T(\frac{N}{2})=2T(\frac{N}{4})+\frac{N}{2}\end{array}\Rightarrow \{\begin{array}{l}T(N)=4T(\frac{N}{4})+2N\\ T(\frac{N}{4})=2T(\frac{N}{8})+\frac{N}{4}\end{array} \\ \Rightarrow ... \\ \Rightarrow T(N)=2^{k}T(\frac{N}{2^k})+kN \\ =NT(1)+N\log N \\ =N\log N+N \\ =O(N\log N) \end{gathered}$$
若$N\ne 2^k$,处理起来更加复杂,但结果类似

4.问题:

六.快速排序
1.基本思想:

"快速排序"(Quick Sort)是在实践中最快的已知排序算法.其平均运行时间为O(N*log N);最坏情形下的运行时间为O(N^2),但稍加努力即可避免这种
情形.不过,在实践中该算法很难编程.和归并排序一样,快速排序也是1种分治的递归算法,步骤如下:
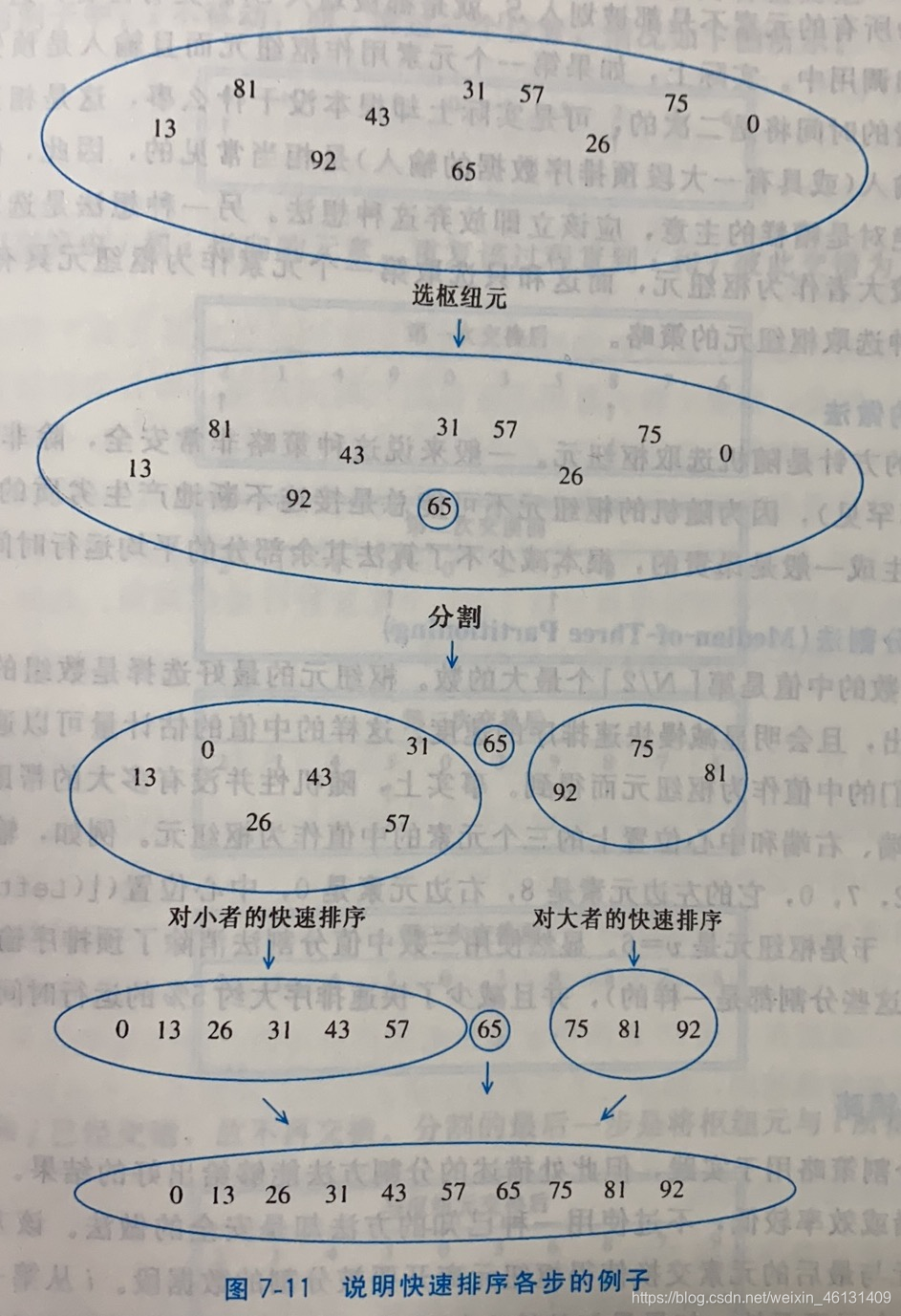
①若S中元素数为0/1,直接返回
②取S中的任意元素v,称为"枢纽元"(Pivot)
③将S-{v}以v为界分为2个不相交的子集S1={x∈S-{v}|x≤v},S2={x∈S-{v}|x≥v}
④结果为{QuickSort(S1),v,QuickSort(S2)}

2.实现
(1)说明:

①选取枢纽元:
  Ⅰ.选取首元素作为枢纽元:若输入是随机的,可以接受;若输入是预排序的,则时间复杂度为O(N^2),但却几乎没有进行任何操作
  Ⅱ.随机选取枢纽元:这种策略通常是安全的,除非随机数生成器有问题;另外,生成随机数通常是昂贵的,可能额外花费大量时间
  Ⅲ.三数中值分割法:选取序列的中值是很困难的,因此使用序列左端/右端/中心位置处的3个元素的中值作为枢纽元.这种方法消除了最坏情况
②分割策略:
  Ⅰ.假设所有元素互异:

(2)实现:

3.算法分析: