美团笔试题练习

1.排序+遍历数组解决问题

读懂题意，不要把此题想的过于复杂，由于淘汰的人数的可能取值，和临界分数 m 一一对应，所以直接遍历排序后的分数数组，并在遍历过程中判断淘汰数量和晋级数量的条件是否满足。最先遍历到满足条件的得分就是所求输出。

#include<bits/stdc++.h>
using namespace std;

int main() {
	int n, x, y, temp, b;
	cin >> n >> x >> y;
	vector<int> a;
	while (cin >> temp) {
		a.push_back(temp);
	}
	sort(a.begin(), a.end());
	for (int i = 0; i < n; i++) {
		b = n - (i + 1);
		if ((i + 1) >= x && (i + 1) <= y && b >= x && b <= y) {
			cout << a[i];
			return 0;
		}
	}
	cout << -1 << endl;

}

---

2、排序+遍历数组解决问题

先对输入的序列进行升序排列。我们需要明白，无论是什么排列的正则序列，改动最少的方案一定是对输入序列和正则序列中相同排名的元素进行修改，即输入序列中排名第 i 的元素应该修改为正则序列中的 i。除此之外，其他的任何方案都至少存在一个数，使得它并不是修改为离它最近的正则序列中的数，这样就会使得修改次数增多。

#include<bits/stdc++.h>
using namespace std;

int main() {
	int n ,res = 0,temp = 0;
	cin >> n;
	vector<int> a;
	while (cin >> temp) {
		a.push_back(temp);
	}
	sort(a.begin(), a.end());
	for (int i = 0; i < n; i++) {
        res += abs(a[i] - i - 1);
	}
	cout << res << endl;

}

---

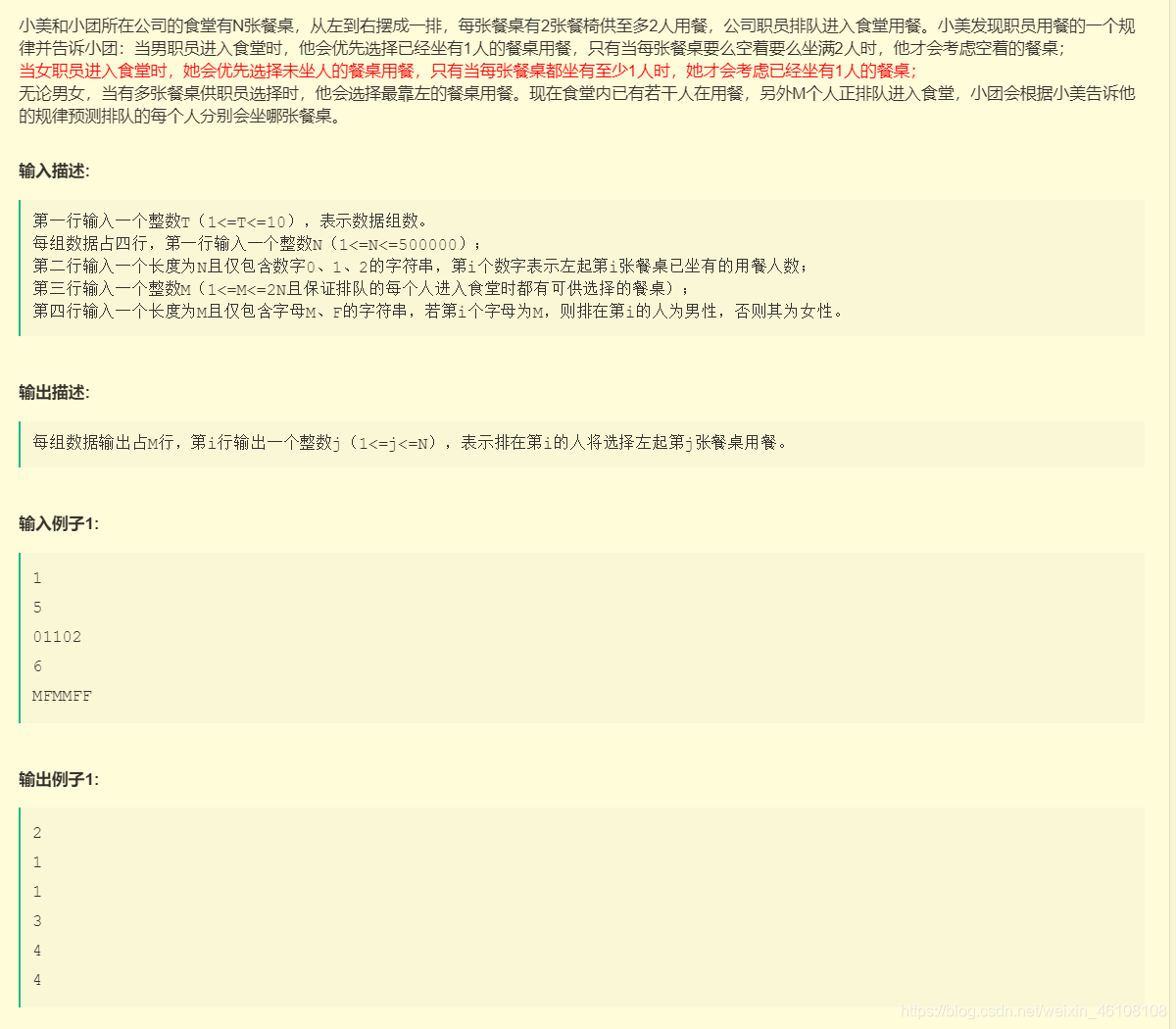
3、排队问题——采用优先队列

拿到此题一看，属于排队问题，假设座位有序号，并且需要序号小的座位先被座，那么，则采用算法复杂的较小的优先队列，并且让它有自动排序功能。

不用管坐了两个人的桌子，坐了0个人的桌子坐了一个人之后出队，入队到坐了一个人的桌子的队列里边；坐了1个人的桌子再坐了一个人之后出队就不用管了

注意：输出换行符用’\n’ 不超时，用endl 则超时。

#include<bits/stdc++.h>
using namespace std;

int main() {
	int T;
	cin >> T;
	while (T--) {
		int N, M;
		string table, people;
		cin >> N;
		cin >> table;
		cin >> M;
		cin >> people;
		priority_queue<int, vector<int>, greater<int>> queue0, queue1;
		for (int i = 0; i < N; i++) {
			int temp = table[i] - '0';
			if (temp == 0)
				queue0.push(i + 1);
			else if (temp == 1)
				queue1.push(i + 1);
		}
		for (auto & x : people) {
			if (x == 'F') {
				if (!queue0.empty()) {
					int res = queue0.top();
					queue0.pop();
					queue1.push(res);
					cout << res << '\n';
				}
				else {
					int res = queue1.top();
					queue1.pop();
					cout << res << '\n';
				}
			}
			else {
				if (!queue1.empty()) {
					int res = queue1.top();
					queue1.pop();
					cout << res << '\n';
				}
				else {
					int res = queue0.top();
					queue0.pop();
					queue1.push(res);
					cout << res << '\n';
				}
			}
		}
	}
}