树与哈希表---最大堆

2022.4.11
发现这个博客有问题，自己并没有(一点没有)掌握这个最大堆

本篇文章很多地方都是我个人所理解，有可能存在很多描述或书写方面的错误，如有还望指出

写在前面,先看Java中的堆

1.什么是堆？

堆实际上就是用数组将一个完全二叉树存起来，堆的主要用途就是用来找集合中的最大值和最小值，每次出去的那个数要么是最大的要么是最小的，当然这个取决于这个堆是大堆还是小堆

这个地方用数组去存储的原因是因为堆是一个完全二叉树，一层层去看，它其实是连续的，并且节点的父子关系可以通过数组的角标去进行表示

2.堆的区分

大堆：第一个数是堆中最大的
小堆：第一个数是堆中最小的

3.Java标准库中的堆的实现

默认是小堆，但是可以通过Comparator接口去使他变成小堆

PriorityQueue<Integer> queue = new PriorityQueue<>();

最大堆

主要了解最大堆的上浮和下沉
上浮操作是用在堆的添加元素
反之
下沉操作是用在堆的删除元素

代码位置:MaxHeap.java

1.初步了解

二叉堆是一颗完全二叉树(区别于满二叉树)（完全二叉树，就是存数据按照空间顺序）

堆中某个结点的值总是不大于其父节点的值

通常这种堆称为最大堆(相应的可以定义最小堆)

下层的某一元素不一定小于上层的某一元素

可以知道的是最上面的那个数一定是最大的，每一个节点都比他的子树中任意一个数大

---

由于这是一颗完全二叉树，所以我们完全可以使用数组去表示

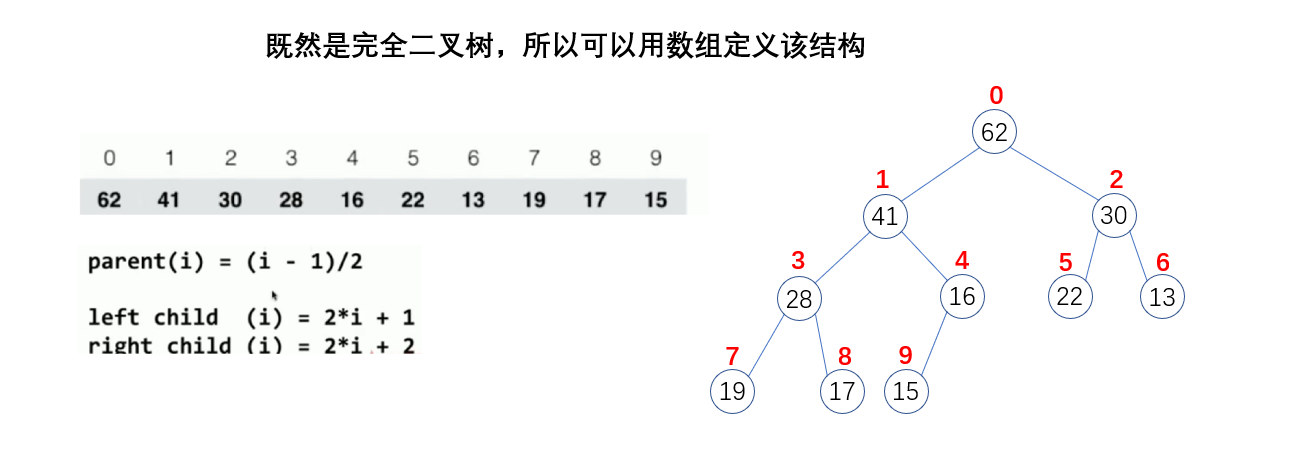
2.一些准备工作

因为代码涉及到上浮和下沉，所以我们需要获取某一个节点的父节点角标和左右子节点角标

获取父节点角标

//获取父节点的角标
private int parent(int index) {
    if (index == 0) {
        throw new IllegalArgumentException("no parent");
    }
    return (index - 1) / 2;
}

获取左孩子的角标

private int leftChild(int index) {
    return 2 * index + 1;
}

获取右孩子的角标

private int rightChild(int index) {
    return 2 * index + 2;
}

3.元素上浮

元素上浮就是将新加进来的元素向上移到它该在的位置
如果该元素比他的父元素大，就将二者交换即可

//元素上浮的操作
private void siftUp(int k) {
    while (k > 0 && data.get(k).compareTo(data.get(parent(k))) > 0) {
        data.swap(k, parent(k));
        k = parent(k);
    }
}

4.元素下沉

元素下沉是发生在删除元素的时候
具体操作过程
想将第一个元素和最后一个元素交换，然后再对当前第一个元素进行下沉操作
此时删除最后一个元素只需要将size--就行了

下沉时需要注意的几点：
一个节点是先有左孩子再有右孩子
如果这个节点左孩子，那么他有可能有右孩子
如果这个节点没有左孩子，那么他这个节点其实就没有子节点

private void siftDown(int k) {
    //如果没有左孩子 同时也就没有右孩子 就不用下沉
    //如果有左孩子 右孩子不一定存在 判断右孩子的存在性
    //如果右孩子存在 取左右两个孩子的最大值和k对应的值比较
    //如果右孩子不存在 只能取左孩子的值和k对应的值比较
    //如果k对应的值比左右两个孩子都大 则不用下沉 否则下沉即可
    while (leftChild(k) < data.size()) {
        // 因为是先左后右,所以先默认j为/左孩子
        int j = leftChild(k);
        // 存在右孩子的情况下,将左右孩子进行比较,取最大的那个
        if (j + 1 < data.size() && data.get(j + 1).compareTo(data.get(j)) > 0) {
            j = rightChild(k);
        }
        // 如果当前值小于 j角标的值 则进行交换,交换完成后 k 的值更新为 j 的值
        if (data.get(k).compareTo(data.get(j)) < 0) {
            data.swap(k,j);
            k = j;
        } else {
            break;  //当前比左右两个孩子都大 不用下沉
        }
    }
}

5.优先队列

通过最大堆实现，很简单