迪杰斯特拉算法（C语言实现)

#include<stdio.h>
#include<string.h>
#include<math.h>

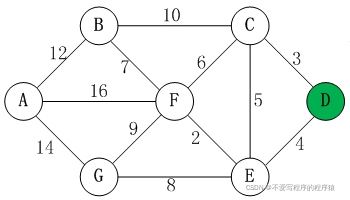
//给定有向/无向加权图G(V, E)，给定源点/起始点s，求从s出发到V中其它所有顶点的权重最小的路径。(迪杰斯特拉算法描述)
/*
算法思路：
1.逐步地发展最短路径树，直至它覆盖所有顶点。
2.构造一个循环，每次循环都增加一个顶点到最短路径树上。
3.从所有与树邻接的顶点中，选择离源点最近的。
4.对每个顶点，都用一个距离标记(Label)来记录。
5.每次循环都需要对距离标记进行更新。

*/
int main(){
   
   
    //使用邻接矩阵构建整个图，其中权重代表传播时延（都是int type），使用INT_MAX(被证明不行，因为加了就溢出了）所以用65535代替，代表图中两个顶点不相连
    int g[7][7] = {
   
               
             65535,12,65535,65535,65535,16,14,	
		     12,65535,10,65535,65535,7,65535,
		     65535,10,65535,3,5