数据结构与算法——动态规划

封底估算

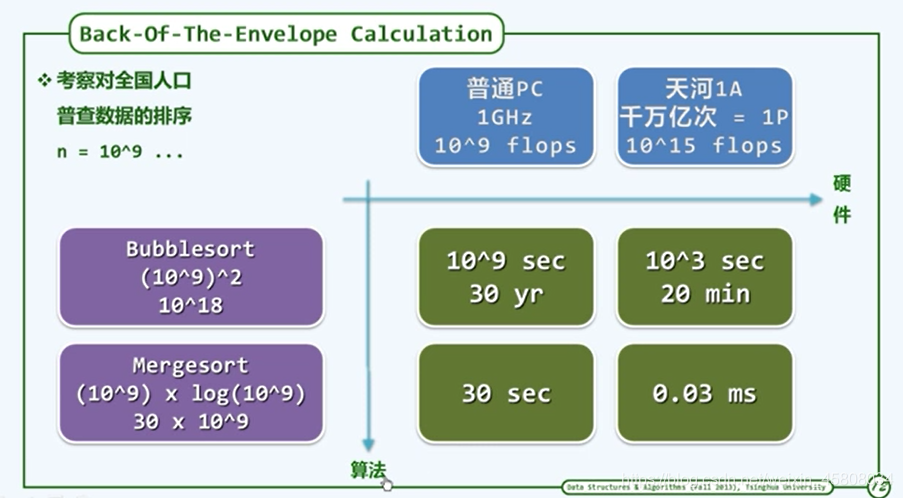
复杂度

算法分析

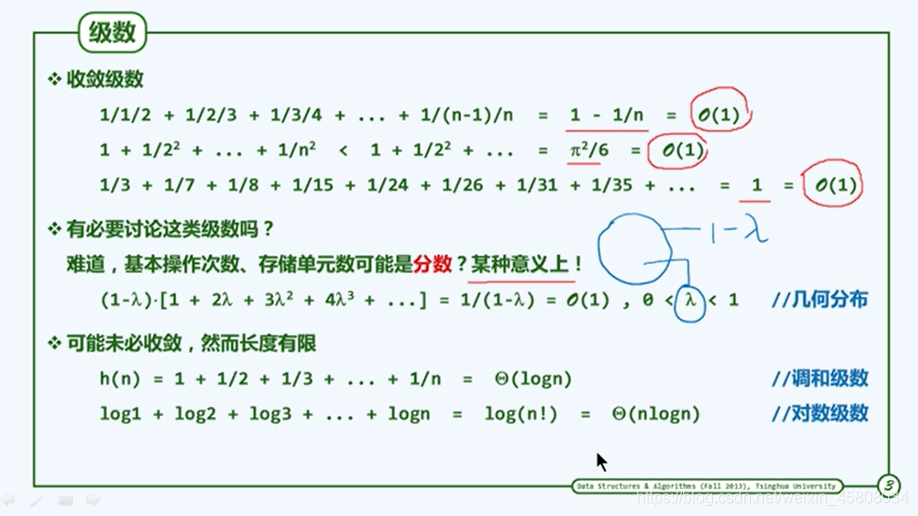
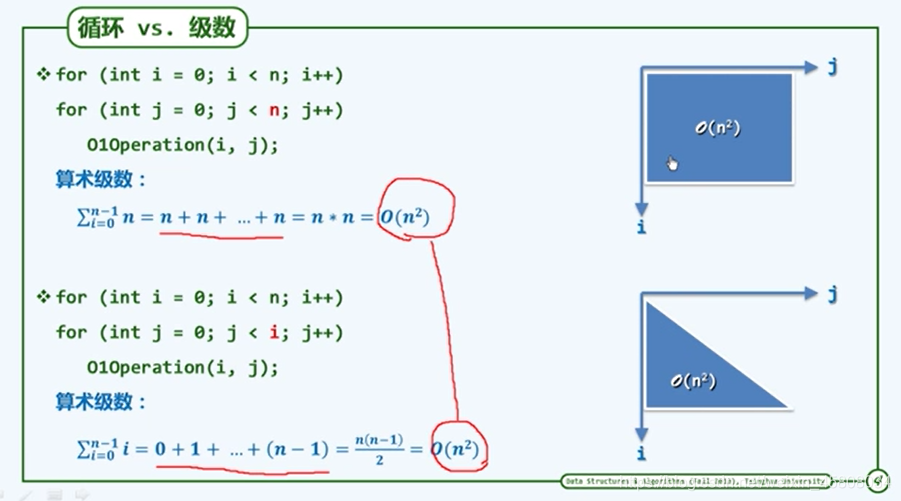
迭代和递归

迭代乃人工，递归方神通
To interate is human, to recurse, divine.

凡治众如治寡，分数是也
The control of a large force is
the same principle as
the control of a few men:
it is merely a question of
dividing up their numbers.

动态规划

动态规划的概念

Make it work,
make it right,
make it fast.
—Kent Beck

前两步可以用递归来解决，后一步可以用迭代来解决。

描述：通过递归找出了算法的本质，并且给出了一个初步的解之后，再将其等效地转化为迭代的形式。

fib():递归

用递归计算Fibonaccis数列的第n项。

fib(n)=fib(n-1)+fib(n-2):{0,1,1,2,3,5,8, ...}

int fib(int n) {  //为何这么慢
	return(2 > n) ? n : fib(n - 1) + fib(n - 2);
}

实现：

#include <iostream>
int fib(int n) {//计算Fibonaccis数列的第n项
	return(2 > n) ? 
				n	//若到达递归基，直接取值 
		: fib(n - 1) + fib(n - 2); //否则，递归计算前两项
}
int main()
{
	int m=64;
	for (int i = 0; i < m; i++) {
		std::cout <<i+1<<"\t"<< fib(i)<< std::endl;
	}
}

fib()递推方程

fib()封底估算

fib()递归跟踪

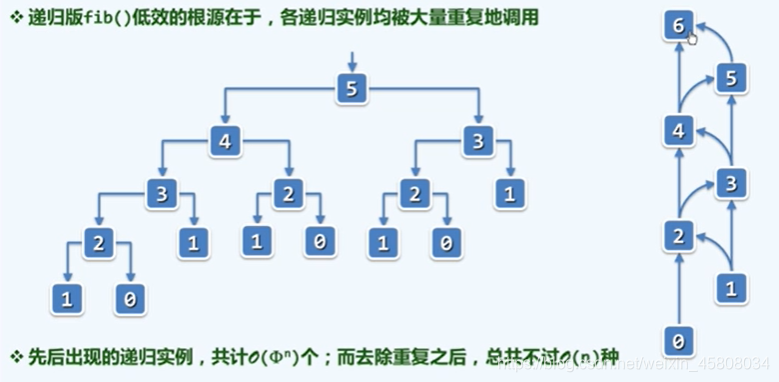
fib()回归迭代

最长公共子序列（LCS）

左上图中的T、N两字符次序紊乱（两条线交叉），无法存在同一序列中，导致出现多种序列构成，所以说可能有多个。
右上图中的D字符的来源有两个，难以判断由哪个d提供，所以说可能有歧义。

递归LCS

理解LCS

通路总长：(n+m-a-b)=(n-a)+(m-b) 。
在 n+m-a-b 下的 n-a ，意味着从 n+m-a-b 这么多条路径中选出 n-a 条水平路径的总数。或者从 n+m-a-b 这么多条路径中选出互补的 m-b 条垂直的路径的总数。

动态规划LCS

以上截图基本来自B站清华邓俊辉老师的课程
截图链接 https://www.bilibili.com/video/BV1db411L71m