超级详细的线段树入门教程【附模板】

一、写在前面

总所周知，线段树作为算法竞赛中最常用的数据结构，是每个oier/acmer的必备技能之一，但对于大部分初学者而言，似乎只要是涉及到树的问题往往让人望而生畏
接下来博主尽量用简单的语言与图示来描述这个超级好用的数据结构，作者水平有限，有错误之处欢迎指出 ~
*（所需前置知识：二叉树基本概念，二分基本思想）

二、单点修改，区间查询（不带懒标记）

来看一个简单的例子：
https://www.luogu.com.cn/problem/P1531

现在给出一个包含n个整数的数组，对该数组进行m次操作
共有两种操作：
第一种操作将第 p 个的元素的值改成 k
第二种操作求出区间 [l, r] 内的最大值并输出

现在来分析这个问题
很显然暴力的做法复杂度高达 $O(nm)$，那么现在考虑来进行优化
假设给出的数组是 {1, 5, 2, 3, 4, 8}
我们很容易发现

max{1, 5, 2, 3, 4, 8} = max(max{1, 5, 2}, max{3, 4, 8}};
max{1, 5, 2} = max{max{1, 5}, 2}, max{2, 4, 8} = max{max{2, 4}, 8}
…

显然，对于一个很大的数组，我们可以用分治的思想进行处理
而且每个父问题的答案都可以由其子问题的答案来更新
这时候线段树就是一个很好的工具

——首先我们考虑构造一颗二叉树，

每个节点存放的是其代表的数组的信息

struct node {
	int l, r;
	int mx;
}tr[N<<2];
//如下图所示，线段树的空间往往不会被充分利用，所以需要开大空间避免越界，一般来说开成N的4倍比较保险

构造的二叉树如图所示：

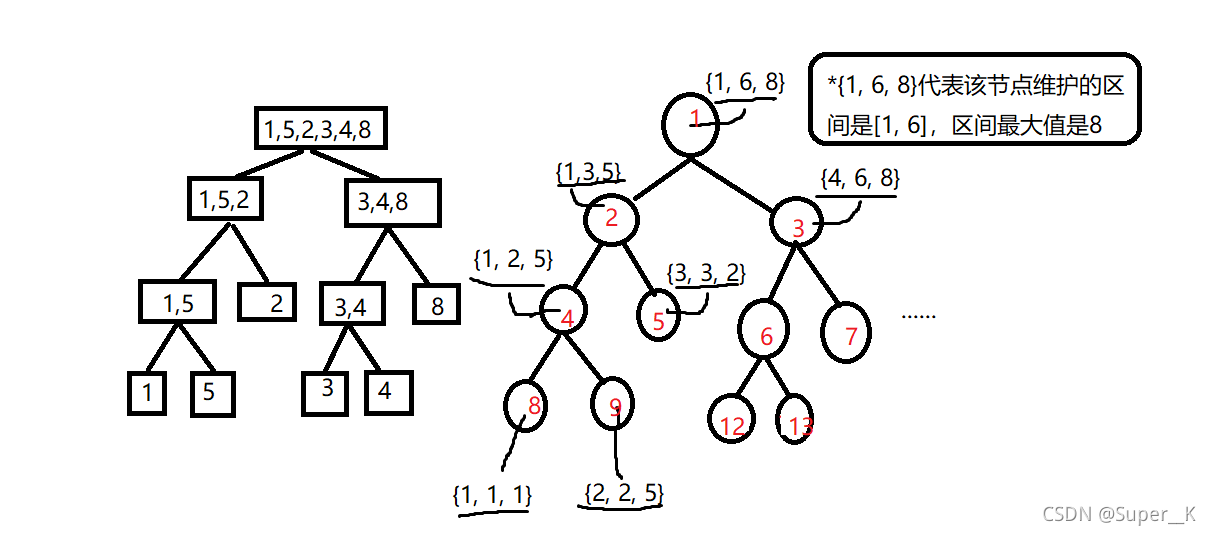
建树大体思路就是我们从最开始的数组（祖先节点）出发，不断将数组二分，直到不能再分（已经是叶节点）时就将其赋值，然后在回溯的过程中运用我们上面所说的，用子节点的信息去更新其父节点的信息，这样我们就得到了一颗线段树，建树的代码如下：

//u<<1等同于u*2(u的左子节点编号), u<<1|1等同于u*2+1(u的右子节点编号)

//pushup()函数表示用子节点去更新父节点的信息
void pushup(int u) {
	tr[u].mx = max(tr[u<<1].mx, tr[u<<1|1].mx);
}
	
void build(int u, int l, int r) {
	//对每个节点进行初始化
	tr[u].l = l, tr[u].r = r;
	tr[u].mx = -INF;
	//若搜到叶子节点则直接赋值
	if (l == r) {
		tr[u].mx = a[l];
		return ;
	} 
	int mid = l+r>>1;
	//建立左子树
	build(u<<1, l, mid);
	//建立右子树
	build(u<<1|1, mid+1, r);
	//回溯时用子节点信息去更新父节点信息
	pushup(u);
}

那么现在我们的线段树已经建好了，接下来需要让给这颗线段树支持修改(update)与查询(query)操作

——分析如何进行单点修改操作

该问题中要求的是单点修改（注意我们已经把数组建成了一颗线段树，所以我们修改时实际上是在对线段树上的节点进行修改）
假设我们要将数组中第p个元素改为k，也就是说我们要找到存储信息为 {p, p, x}的这个叶节点，然后将 x修改为 k
因为数组的位置是递增的，所以我们可以用二分的方法找到位置p，于是我们从祖先节点{1, n, x}开始向下搜索 ，具体update()代码如下

void update(int u, int p, int k) {
	//找到了要修改的叶节点
	if (tr[u].l == tr[u].r) {
		tr[u].mi = k;
		return ;
	}
	//二分搜索
	int mid = tr[u].l+tr[u].r>>1;
	if (p <= mid) {
		update(u<<1, p, k);	
	} else {
		update(u<<1|1, p, k);
	}
	//注意子节点被修改后，其父节点的信息也要及时更新
	pushup(u);
}

——分析如何进行区间查询操作

假设我们要查询的目标区间是[l, r] ，因为线段树中每个节点都代表一个子区间，所以在线段树中一定有一些节点，这些节点所代表的子区间合并后恰好等于[l, r]
那么我们同样可以用二分的方法找到这些子区间，并得到他们的最大值，其即为[l, r]中的最大值（如图，区间[2, 5]中的最大值实际上就是三个绿色节点的最大值）

具体代码如下：

int query(int u, int L, int R) {
	//若要查询的目标区间[L, R]包含当前的节点代表的区间[l, r]
	if (tr[u].l>=L && tr[u].r<=R) {
		return tr[u].mx;
	}
	//二分搜索
	int mid = tr[u].l+tr[u].r>>1;
	int res = -INF; 
	if (mid >= L) 
		res = max(res, query(u<<1, L, R));
	if (mid < R)
		res = max(res, query(u<<1|1, L, R));
	return res;
} 

最后将这些代码整合起来就得到了我们所需要的数据结构！可以进行单点修改+区间查询最值，时间复杂度仅为 $O(mlogn)$ 【模板放在文章末尾】

如果理解了这个过程，可以尝试解决我放在文章开头的例题~
那么我们解决了单点修改的问题，接下来看看如何解决区间修改的问题 ~

三、区间修改，区间查询（带懒标记）

——分析如何进行区间修改操作

假设我们将上面问题的操作一改为将某个区间的所有元素的值加上 k，那么该如何操作？
我们可以根据上面的查询操作来进行类似的思考，将修改区间 [l, r] 转化为修改线段树上的节点信息，但如果我们对区间 [l, r] 的每个值都进行单点修改，显然效率并不高，我们会发现其实我们修改某个节点所维护的区间时，其实不一定需要对其子节点所维护的区间也进行修改，因为我们并不一定会用上其子节点的信息。

这里举个例子，如果我们将区间 [2, 5] 的所有元素加上k，相当于将区间 [2, 5] 的最大值加上k。若我们要查询区间 [1, 5] 的最大值，我们发现查询其实只需要 [1, 1] 和 [2, 5] 的区间信息即可，就没有必要去查询例如 [2, 3]，[3, 5] 等子区间的信息，所以修改时这些子区间的信息是没有必要修改的

于是这里我们引入懒标记的概念，我们给要修改的区间打上一个懒标记，这样就不用再去修改其子节点所维护的的区间，只有当我们需要使用其子节点所维护区间的信息时，再将懒标记下传更新即可。这样只有我们就可以满足用到哪一个节点就更新哪一个节点，避免了大量无意义的操作，极大提升了修改的效率

这部分看起来可能会比较抽象，可以结合代码来理解

//节点u接收其父节点传输的懒标记tag
void eval(int u, int tag) {
		tr[u].tag += tag;
		tr[u].mx += tag;
}

//下传操作，与pushup()相反，相当于由父节点更新子节点信息
void pushdown(int u) {
	eval(u<<1, tr[u].tag);
	eval(u<<1|1, tr[u].tag);
	//下传后记得将当前节点的懒标记清空
	tr[u].tag = 0;
}

void update(int u, int l, int r, int k) {
    if (l<=tr[u].l && r>=tr[u].r) {
        eval(u, k);
		return;
    }
    //每次搜索节点u的子节点时注意要同时下传节点u的懒标记
    pushdown(u);
    int mid = tr[u].l+tr[u].r>>1;
    if (l <= mid) 
		update(u<<1, l, r, k);
    if (r > mid) 
		update(u<<1|1, l, r, k);
	//回溯时由子节点更新父节点信息
    pushup(u);
}

——分析如何进行区间查询操作

整体思路和上面单点修改的区间查询操作一致，但是要注意查询节点u的子节点时也不要忘了同时向其子节点下传懒标记(pushdown)，以及子节点信息被懒标记更新后父节点的信息也要进行更新(pushup)

int query(int u, int l, int r) {
	if (l <= tr[u].l && r >= tr[u].r) 
		return tr[u].mx;
	pushdown(u);
	int mid = tr[u].l+tr[u].r>>1;
	int res = 0;
	if (l <= mid) 
		res = max(res, query(u<<1, l, r));
	if (r > mid) 
		res = max(res, query(u<<1|1, l, r));
	pushup(u);
	return res;
}

四、线段树基础模板

*不带懒标记基本线段树（以单点修改，区间求最值为例）

struct SegmentTree {
	struct node {
		int l, r, mi;
	}tr[N<<2];
	void pushup(int u) {
		tr[u].mi = min(tr[u<<1].mi, tr[u<<1|1].mi);
	}
	void build(int u, int l, int r) {
		tr[u].l = l, tr[u].r = r;
		tr[u].mi = INF;
		if (l == r) {
			tr[u].mi = a[r];
			return ;
		}
		int mid = l+r>>1;
		build(u<<1, l, mid);
		build(u<<1|1, mid+1, r);
		pushup(u);
	}
	void update(int u, int p, int k) {
		if (tr[u].l == tr[u].r) {
			tr[u].mi = k;
			return ;
		}
		int mid = tr[u].l+tr[u].r>>1;
		if (p <= mid) {
			update(u<<1, p, k);	
		} else {
			update(u<<1|1, p, k);
		}
		pushup(u);
	}
	int query(int u, int L, int R) {
		if (tr[u].l>=L && tr[u].r<=R) {
			return tr[u].mi;
		}
		int mid = tr[u].l+tr[u].r>>1;
		int res = INF; 
		if (mid >= L) 
			res = min(res, query(u<<1, L, R));
		if (mid < R)
			res = min(res, query(u<<1|1, L, R));
		return res;
	} 
}tree;

*带懒标记基本线段树（以区间修改，区间求最值为例）

struct SegmentTree {
	struct node {
	    int l, r;
	    int mx, tag;
	}tr[N<<2];
	
	void inline pushup(int u) {
	    tr[u].mx = max(tr[u<<1].mx, tr[u<<1|1].mx);
	}
	
	void eval(int u, int tag) {
		tr[u].tag += tag;
		tr[u].mx += tag;
	}
	
	void pushdown(int u) {
		eval(u<<1, tr[u].tag);
		eval(u<<1|1, tr[u].tag);
		tr[u].tag = 0;
	}
	
	void build(int u, int l, int r) {
		tr[u].l = l, tr[u].r = r;
		tr[u].tag = 0, tr[u].mx = -0x3f3f3f3f;
	    if (l == r) {
	    	tr[u].mx = w[l];
	    	return ;
		}
	    int mid = l+r>>1;
	    build(u<<1, l, mid);
		build(u<<1|1, mid+1, r);
	    pushup(u);
	}
	
	void update(int u, int l, int r, int k) {
	    if (l<=tr[u].l && r>=tr[u].r) {
	        eval(u, k);
			return;
	    }
	    pushdown(u);
	    int mid = tr[u].l+tr[u].r>>1;
	    if (l <= mid) 
			update(u<<1, l, r, k);
	    if (r > mid) 
			update(u<<1|1, l, r, k);
	    pushup(u);
	}
	
	int query(int u, int l, int r) {
	    if (l <= tr[u].l && r >= tr[u].r) 
			return tr[u].mx;
	    pushdown(u);
	    int mid = tr[u].l+tr[u].r>>1;
	    int res = 0;
	    if (l <= mid) 
			res = max(res, query(u<<1, l, r));
	    if (r > mid) 
			res = max(res, query(u<<1|1, l, r));
		pushup(u);
	    return res;
	}
}tree;