Copula(2)

Copula(2)—椭圆类copula

Copula函数的分类

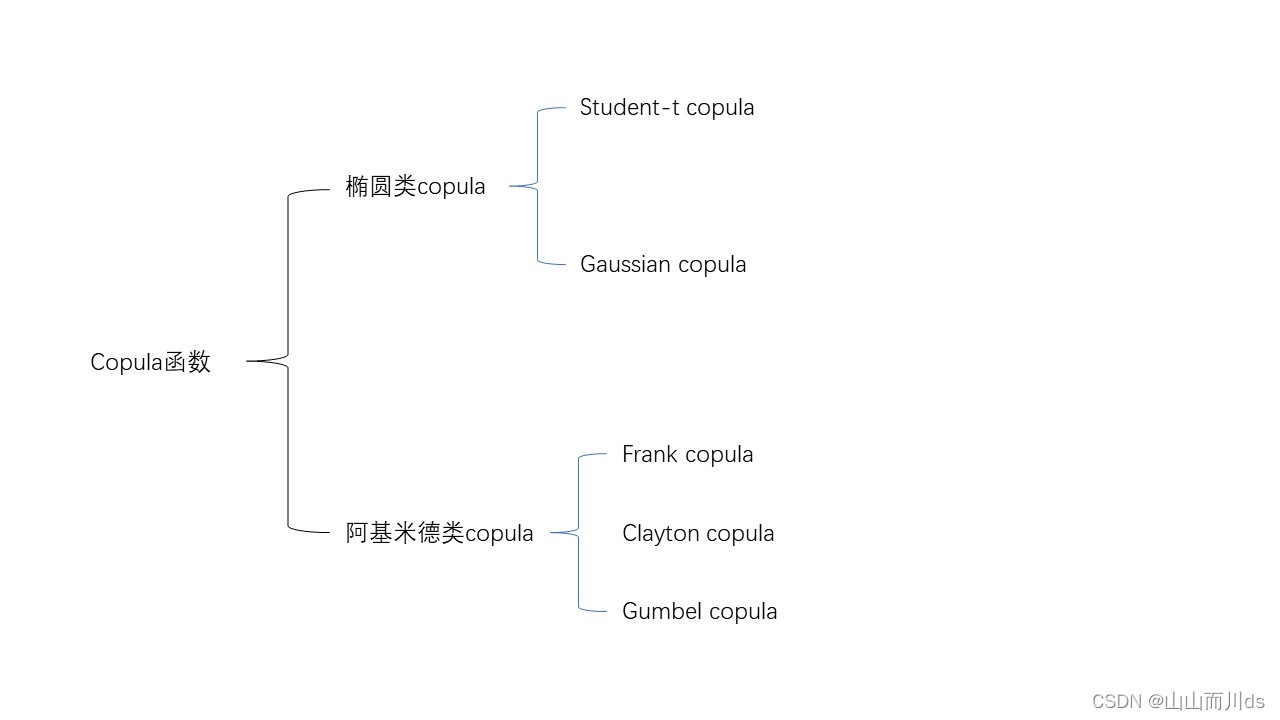
研究中使用最多的 Copula 函数主要有阿基米德 Copula 和椭圆类 Copula。
椭圆copula:优点在于简单性以及在做模拟基于分布的copula时比较方便，但是缺点在于需要对多个参数进行估计。
阿基米德copula:copula函数具有显示表达式，但是进行多元拓展的话是比较麻烦的。

椭圆类copula

椭圆类copula就包含Gaussian copula和student-t copula。本文以两个变量为例，研究变量$X,Y$的某种关系，利用copula函数估计他们的联合分布。假设$F,G$分别是它们的边际分布函数，令$u=F(x),V=G(y)$

Gaussion copula

Gaussion copula密度函数形式如下：
$$c(u,v)=\frac{1}{|R{|}^{1/2}}exp-\frac{1}{2}{\psi }^{\prime }(R^{-1}-I_2)\psi$$
其中$\psi =({\Phi }^{-1}(u),{\Phi }^{-1}(v){)}^{\prime }$,$\Phi$是单变量标准正态分布函数，$R$是变量之间的相关系数矩阵，$I_2$是2为单位矩阵。
在两变量的情况下，R矩阵的表达式为：
$$\left[\begin{array}{cc}1& \rho \\ \rho & 1\end{array}\right]$$
下面解释$\rho$是什么的线性相关函数
假设$X,Y$映射到$W,Z$,那么我们可以得到$N(w)=F(x),N(z)=G(y)$，将上述的式子进行改写，$W=N^{-1}(F(x)),Z=N^{-1}(G(y))$,这个$\rho$表示的就是W,Z的线性相关系数，也是$N^{-1}(F(x))，N^{-1}(G(y))$的线性相关系数
Gaussian copula函数
$$C(u,v)={\Phi }_2({\Phi }^{-1}(u),{\Phi }^{-1}(v))={\int }_{-\infty }^{{\Phi }^{-1}(u)}{\int }_{-\infty }^{{\Phi }^{-1}(v)}\frac{1}{|R{|}^{1/2}}exp-\frac{1}{2}{\psi }^{\prime }(R^{-1}-I_2)\psi dvdu$$
其中${\Phi }_2(\cdot ,\cdot )$是双变量的标准Gaussion分布函数

下面我们将二元的Gaussion copula拓展到多元的一个情况
多元Gaussion copula函数
$$\begin{array}{rl}c(u_1,u_2,...,u_n;\Sigma )& ={\Phi }_{\Sigma }({\Phi }^{-1}(u_1),...,{\Phi }^{-1}(u_n))\\ & ={\int }_{-\infty }^{{\Phi }^{-1}(u_1)}...{\int }_{-\infty }^{{\Phi }^{-1}(u_n)}\frac{1}{(2\pi {)}^{\frac{d}{2}}|\Sigma {|}^{1/2}}exp(-\frac{1}{2}{W}^T{\Sigma }^{-1}W)dW\end{array}$$

多元Gaussion copula密度函数
c(u1,u2,...,un;Σ)=∂C(u1,u2,...,un;Σ)∂u1...∂un=1∣Σ∣1/2exp{−12[Φ−1(u1),...,Φ−1(un)]Σ−1(Φ−1(u1)...Φ−1(un))+12∑i=1n(Φ−1(ui))2}\begin{aligned} c(u_1,u_2,...,u_n;\Sigma) &=\frac{\partial C(u_1,u_2,...,u_n;\Sigma)}{\partial u_1 ... \partial u_n} \\ &=\frac{1}{|\Sigma|^{1/2}}exp\{-\frac{1}{2}[\Phi^{-1}(u_1),...,\Phi^{-1}(u_n)]\Sigma^{-1}\begin{pmatrix}\Phi^{-1}(u_1) \\ ... \\ \Phi^{-1}(u_n)\end{pmatrix}+ \frac{1}{2}\sum_{i=1}^n(\Phi^{-1}(u_i))^2\} \end{aligned}c(u1​,u2​,...,un​;Σ)​=∂u1​...∂un​∂C(u1​,u2​,...,un​;Σ)​=∣Σ∣1/21​exp{−21​[Φ−1(u1​),...,Φ−1(un​)]Σ−1​Φ−1(u1​)...Φ−1(un​)​​+21​i=1∑n​(Φ−1(ui​))2}​
后续给出Gaussion copula函数下，关于原始变量的秩相关系数以及尾部相依性的表达式:
$$\begin{gathered} Kendall秩相关系数:\tau =\frac{2}{pi}\arcsin (\rho ) \\ Spearman秩相关系数:\varrho =\frac{2}{\pi }\arcsin (\frac{\rho }{2}) \\ 上下尾相依系数:{\lambda }_u={\lambda }_l=0 \end{gathered}$$
因此Gaussion copula函数无法研究变量之间的尾部相依性。

student-t copula

student-t函数的密度函数
$$c_{\rho ,n}(u,v)=\frac{1}{\sqrt{|R|}}\frac{\Gamma (\frac{n+2}{2})\Gamma (\frac{n}{2})}{\Gamma (\frac{n+1}{2}{)}^2}\frac{(1+\frac{1}{n}{\psi }^{\prime }{R}^{-1}\psi {)}^{-\frac{n+2}{2}}}{{\prod }_{i=1}^2(1+\frac{1}{n}{\psi }_i^2{)}^{-\frac{n+1}{2}}}$$
其中$\psi =(t_n^{-1}(u),t_n^{-1}(v){)}^{\prime }$,$t_n$是单变量的自由度为n的student-t分布，R是变量之间的线性相关系数矩阵。
在student-t分布中，需要待估的参数为相关系数矩阵以及自由参数。

student-t函数
$$\begin{array}{rl}{C}_{\rho ,n}(u,v)& =t_{\rho ,n}(t_n^{-1}(u),t_n^{-1}(u))\\ & ={\int }_{-\infty }^{t_n^{-1}(u)}{\int }_{-\infty }^{t_n^{-1}(v)}\frac{\Gamma (\frac{n+2}{2})}{\Gamma (\frac{n}{2})\pi n\sqrt{1-{\rho }^2}}(1+\frac{{\psi }^{\prime }{R}^{-1}\psi }{n}{)}^{-\frac{n+1}{2}}\end{array}$$

同样的，将student-t copula延申到多元的情况，我们得到
student-t copula分布函数
$$\begin{array}{rl}c(u_1,u_2,...,u_d;\Sigma ,v)& =T_{\sigma ,v}(T_v^{-1}(u_1),...,T_v^{-1}(u_d))\\ & ={\int }_{-\infty }^{T_v^{-1}(u_1)}...{\int }_{-\infty }^{T_v^{-1}(u_d)}\frac{\Gamma (\frac{v+d}{2})}{\Gamma \frac{v}{2}(\pi v{)}^{\frac{d}{2}}|\Sigma {|}^{\frac{1}{2}}}(1+\frac{W^T{\Sigma }^{-1}W}{v}{)}^{-\frac{v+d}{2}}dW\end{array}$$

阿基米德copula

在本文中，我们主要介绍三种阿基米德copula:Frank copula,Clayton copula,Gumbel copula
在双变量情况下，阿基米德copula表示形式为：
$$C(u,v)={\psi }^{-1}(\psi (u)+\psi (v))$$
其中，$\psi :[0,1]\to [0,\infty ]$，为连续且严格单调递减的凸函数，${\psi }^1=0$,称为copula的生成函数，在${\psi }^{-1}$满足二次连续可导的条件下，其密度函数为
$$c(u,v)=\frac{{\psi }^{\prime \prime -1}(\psi (u)+\psi (v))}{{\psi }^{\prime -1}({\psi }^{\prime }(u)){\psi }^{\prime -1}({\psi }^{\prime }(v))}$$

Frank copula

当$\psi (t)=log(e^{-\theta }-1)-log(e^{-\theta t}-1)$时，其中待估参数$\theta \ne 0$,我们可以得到Frank copula以及其密度函数
$$\begin{gathered} Frankcopula:C_{\theta }(u,v)=-\frac{1}{\theta }(1+\frac{(e^{-\theta u}-1)(e^{-\theta v}-1)}{e^{-\theta }-1}) \\ Frankcopula密度函数:c_{\theta }(u,v)=\frac{\theta (1-e^{-\theta })e^{-\theta (u+v)}}{[(1-e^{-\theta })-(1-e^{-\theta u})(1-e^{-\theta v}){]}^2} \end{gathered}$$
原始变量的秩相关系数以及尾部相依性的表达式为：
$$\begin{gathered} Kendall秩相关系数:\tau =1-4\frac{1-D_1(\theta )}{\theta } \\ Spearman秩相关系数:\varrho =1-12\frac{D_1(\theta )-D_2(\theta )}{\theta } \end{gathered}$$
其中，
$$D_k(x)=\{\begin{array}{l}\frac{k}{x^k}{\int }_0^x\frac{t^k}{e^t-1}dt,ifx\ge 0\\ \frac{k|x|}{1+k}+\frac{k}{|x{|}^k}{\int }_x^0\frac{t^k}{e^t-1}dt,ifx<0\end{array}$$
对于Frank copula的上、下尾相依系数的计算，发现其上、下尾相依系数都为0。表明Frank copula尾部相依性是对称的且渐进独立的。

Clayton copula

当$\psi (t)=(t^{-\theta }-1)/\theta$，其中$\theta \in (0,\infty )$,则Clayton copula以及其密度函数为：
$$\begin{gathered} Claytoncopula{C}_{\theta }(u,v)=(u^{-\theta }+v^{-\theta }-1{)}^{-1/\theta } \\ Claytoncopula密度函数c_{\theta }(u,v)=(1+\theta )(uv{)}^{-\theta -1}(u^{-\theta }+v^{-\theta }-1{)}^{-2-1/\theta } \end{gathered}$$
原始变量的秩相关系数以及尾部相依性的表达式为：
$$\begin{gathered} Kendall秩相关系数:\tau =\frac{\theta }{\theta +2}上尾相依系数：{\lambda }_u=0 \\ 下尾相依系数：{\lambda }_l=2^{-\frac{1}{\theta }} \end{gathered}$$
因为带估参数大于0，所以Clayton copula不允许负相依性。从上、下尾相依系数可以看出，Clayton Copula呈现出强的下尾相依性，而上尾相依性渐进独立。
Clayton copula函数被广泛应用在保险和风险管理领域，刻画金融市场熊市期间的下尾相依性。

Gumbel copula

当$\varphi (t)=(-\log t{)}^{\theta }$,其中待估参数$\theta \in [1,\infty )$,则Gumbel copula以及其密度函数为：
$$\begin{gathered} Gumbelcopula:C_{\theta }(u,v)=exp-[(-logu{)}^{\theta }+(-logv{)}^{\theta }{]}^{1/\theta } \\ Gumbelcopula密度函数:c_{\theta }(u,v)=\frac{C_{\theta }(u,v)[logu\ast logv{]}^{\theta -1}}{uv[(-logu{)}^{\theta }+(-logv{)}^{\theta }{]}^{2-1/\theta }}\ast -[(-logu{)}^{\theta }+(-logv{)}^{\theta }{]}^{1/\theta }+\theta -1 \end{gathered}$$
原始变量的秩相关系数以及尾部相依性的表达式为：
$$\begin{gathered} Kendall秩相关系数:\tau =1-\frac{1}{\theta } \\ 上尾相依系数：{\lambda }_u=2-2^{\frac{1}{\theta }} \\ 下尾相依系数：{\lambda }_l=0 \end{gathered}$$
因为待估参数大于等于1，因此Gumbel copula不允许负相依性。从上、下尾相依系数可以看出，Gumbel copula呈现出强的上尾相依性，而下尾相依性渐进独立。
Gumbel Copula函数常用于刻画在“牛市”时期金融市场之间的上尾相依性。