FasterMoE:Modeling and Optimizing Training of Large-Scale Dynamic Pre-Trained Models
FasterMoE阅读笔记
b站报告视频:FasterMoE-何家傲
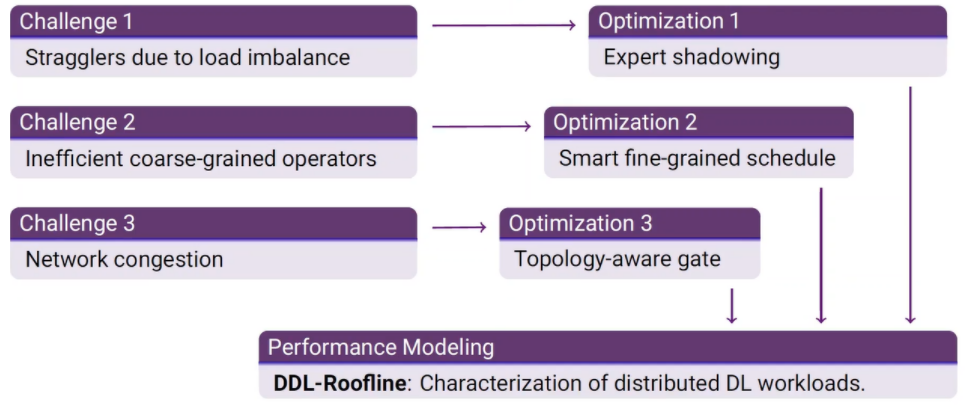
一、论文背景、动机、主要贡献
论文背景
Note:之前阅读的两篇论文:Alpa和Pathways都说明了目前深度学习模型规模逐渐变大的背景;参考RNN相关背景知识:大模型意味着有更多的参数,更多的参数能够给模型带来准确性的提高,这是为什么AI模型越来越大的原因。
混合专家(Mixture-of-Expert,MoE):目前最流行的预训练模型,使训练万亿级别以上的参数模型变得可能。MoE由许多小模型组成,即专家模型。
- 小模型:计算力有限;大模型:计算量昂贵
- MoE:采用了另一种思路,使用门模块(Gate Module)选择专家,达到以下效果:
- 模型大小被扩大,模型能力增强
- 专家是稀疏激活的,节省了额外的计算量
Note:
MoE论文链接:MoE论文本地链接
关于预训练模型(Pre-Trained Model):预训练模型是一类已在较大的数据集上训练好的模型,这类模型往往比较大,训练需要耗费大量的内存资源。比如NLP中常见的预训练模型Bert和GPT。预训练模型训练结束时的结果较好的一组参数值可以迁移到其他的网络中,其他的网络便学习了这个网络的特征和其拥有的知识。
[详解预训练模型](详解预训练模型 ——从词向量到GPT模型_抚顺菜市场的博客-优快云博客_预训练模型)
与经典的密集预训练模型相比,MoE可以显著增加同一时间段内训练的样本数量,提高模型的精度。因此,这种动态模型对于训练一个巨型模型越来越重要。

论文动机
虽然上述的MoE使得训练万亿规模的巨型模型变得可行,但是成本依然很高:GShard中一个6000亿的MoE模型需要2048 个tpu花费4天的时间来训练。为了减少训练时间,引入了专家并行(expert parallelism):专家分布在不同的工作节点(worker)上,每个工作节点(worker)处理不同批次的训练样本。
如下图,MoE采取**专家并行**的模式,所有的专家被放到各个worker上,训练的数据(data, tokens)类似于数据并行,也被分布式地分布在各个worker上。图中出现了两次的all-to-all通信:输入端的all-to-all将数据(tokens)发送到期望的专家处,经过专家在各个worker上分布式地训练数据后,在输出端通过all-to-all送回原来的序列位置。

但MoE也给训练的系统带来了挑战:
-
动态负载不平衡(dynamic load imbalance)
存在某个专家更“受欢迎”,
all-to-all操作后,较多的数据会被发送到该专家处,造成负载不均衡。此外,在不同的迭代轮次中,这种模式会发生变化,进一步影响了硬件的利用率和训练效率。 -
低效的同步执行模式(inefficient synchronous execution mode)
粗粒度的计算是低效的,计算和通信二者之一始终存在空闲。考虑到不统一的专家选择会导致计算和通信的严重不平衡,这种启动同步操作的方法会导致更多的开销。
-
拥塞的
all-to-all通信结点(Node)内部的worker之间通信较为高速,结点之间的通信常使用以太网等,带宽有限。在
token分布均匀的情况下,结点之间的通信将会十分密集,造成拥塞。
论文贡献
针对上述的问题,分别给出了针对性解决方法:
(1)性能模型
该模型能够准确预测特定的训练任务的不同操作的延迟,也能使用一个屋顶线型模型(roofline-like model)直观分析端到端的性能。
处理动态负载不平衡的问题。
(3)智能细粒度调度(Smart fine-grained schedule)
将不同的操作分隔并并发执行。
(4)拥塞避免专家选择策略
在允许修改专家选择的情况下,以较低的迭代延迟缓解网络拥塞。
将以上的方法集成作为一个通用的系统:FasterMoE。该系统在不同的集群系统上进行评估,最多使用了 64 个GPU。与大型模型的最先进系统(包括ZeRO、GShard和基础层)相比,它实现了1.37 - 17.87的加速。
Note:Source code of FasterMoE is now available at https://github.com/thu-pacman/FasterMoE.
二、问题定义和描述
Transformer:使用MoE扩展MLP
Transformer是处理序列的最先进结构。一个Transformer Block 由Attention层和多层感知机(MLP)两组成。Attention层的结果被送入MLP层后,该层由两个巨大的全连接(FC)层组成。Transformer Block 中最耗时的计算是发生在MLP层的一般矩阵乘法(GeMM)。在 Transformer 中,MLP层通常用MoE扩展。
在non-MoE Transformer模型中,MLP中有两个相邻的FC层。当模型规模扩大时,这些密集的层变得巨大,使得GeMM的计算量过大。在MoE模型中,GeMM的权重矩阵沿着一定的维数分割,使得每个部分仍然产生相同大小的输出,而GeMM的计算量仍然很小。换句话说,MoE允许在不增加计算量的情况下增加模型参数,这使得它成为目前生产万亿级以上预训练模型的最可行方法。

对于一个给定的输入,一个额外的模块,门,被引入来决定哪些专家应该被激活。gate通常是一个小的FC层,用于计算每个专家的匹配分数,并选择匹配分数最高的前 k 个专家。

并行策略
数据并行、模型并行和专家并行是分布式训练中常见的三种并行策略。
-
数据并行(Data Parallelism)
在所有的worker上复制数据,给每个worker不同批次的训练样本。worker在每一次迭代后全局同步变化并更新模型。尽管在每轮迭代中没有通信,但是模型的大小不能超过单个worker的能力范围,这使模型的大小受限。
-
模型并行(Model Parallelism)
按照一定的维度分割权重向量,即模型被分区并放置在不同的worker上。所有的worker一起处理全局批处理,使用相应部分的权重划分进行计算。在每一层后,对嵌入的向量进行聚合和再分布。但是,模型的并行性受限于分区维度和层与层之间通信开销大的限制,无法高效地扩展到非常大的模型。
-
专家并行(Expert Parallelism)
首先被GShard提出,是一种针对MoE的特殊并行方式。专家分布在不同的worker上,并且每个worker承担不同批次的训练数据。对于非MoE层来说,专家并行和数据并行一样。在MoE层中,序列中的token被发送到它们渴望的专家处。与模型并行相似,每个MoE层的输出被再次交换,重新组织成原始序列,用于下一层的计算。由于MoE模型通常有大量的专家,专家并行度比模型并行度更能随模型规模的增大而增大。

MoE策略的挑战
主要对三个影响MoE性能的挑战进行详细描述。
倾斜的专家选择(Skewed expert selection)
以Figure3为例,专家0收到3个token,比专家2多3个工作负载。结果,worker 2在下一次通信开始之前很长一段时间处于空闲状态,没有充分利用其可用的计算能力。考虑到训练数据自然遵循倾斜分布,一些专家比其他人更有可能被选中。
另外,如Figure 4(a)所示的MoE层中,专家的受欢迎程度在整个培训过程中都在不断变化。图4b展示了不同模型中的另一层,在这一层中,受欢迎程度更稳定,但仍然有很多不受欢迎的专家,特别的,放大图,可以看到虽然这些专家不受欢迎,但仍忠心的处理着相应领域的数据。


更受欢迎的专家比不受欢迎的专家收到的 token 更多,这让它们所在的worker负担更重。因此,MoE续联系统面临的第一个挑战是如何处理倾斜专家选择造成的动态负载不平衡。
同步执行模式效率低(Synchronous execution mode of operations)
考虑到不统一的专家选择会导致计算和通信的不平衡,这种同步执行方法会造成更高的资源浪费。当执行通信或计算时,其他硬件最终没有得到充分利用,而它们可以用于处理其他操作。

但是,由于通信和计算之间存在依赖关系,因此很难分割到所有的通信。如果传输的顺序不合理,那么很容易造成死锁。因此,第二个挑战是如何有效地组织通信和计算任务并行执行。
网络拥塞与竞争(severe network contention)
最后是专家任务与网络拓扑之间的不协调性。每个Node内部Worker之间连接是高带宽的,但是Worker与Worker之间由于使用的是以太网等通信方式,如果不对专家选择进行约束,那么在数据分布较平衡的情况下Worker与Worker之间的通信更密集,造成拥塞。因此,第三个挑战是如何设计一种网络拓扑感知token分配策略,以避免严重的网络争用。

性能建模
为了评估和分析训练任务的性能,首先分别引入建立的计算模型和通信模型。然后,进一步建立一个类似屋顶线的模型来研究通信延迟和计算延迟是如何共同影响整体训练效率的。符号标记:

Load-aware计算建模
GeMM是训练Transformer时的主要计算。现代大规模的计算设备对常规的计算,如GeMM运行进行了大量优化,甚至实现了峰值吞吐量的90%以上。使用下面公式预测Transformer中MLP层正向计算的时延:
L
a
t
comp
=
max
w
∈
workers
{
4
B
w
α
H
2
P
w
}
L a t_{\text {comp }}=\max _{w \in \text { workers }}\left\{\frac{4 B_{w} \alpha H^{2}}{P_{w}}\right\}
Latcomp =w∈ workers max{Pw4BwαH2}
B
w
B_w
Bw:worker w的批大小
H H H:输入的token向量的长度
α H \alpha H αH:MLP中两个FC层之间的向量的长度
P w P_w Pw:w个worker进行GeMM的平均吞吐量
由于单个FMA操作(混合乘加运算)占用两个操作,因此每次FC执行将占据 2 B w α H 2 2B_w\alpha H^2 2BwαH2个操作。由于有两个FC层,故系数为4。端到端延迟是每个worker的最大延迟,因此该公式反映计算中的负载不均衡。
Topology-aware通信建模
通信的整体延迟由通信开销和延迟组成。
Note:LogP模型描述计算机系统的并行计算模型
- Latency(信息从源到目的地所需的时间)
- Overhead(处理器接受或发送一条消息所需额外开销,并且在此期间处理器不能做作任何操作)
- Gap(处理器连续进行两次发送或接收消息之间必须有的时间间隔)
- Processor(处理器的数目)
LogP模型中,网络的容量是有限度的 , 在任何时刻的网上 , 从任何处理器发出或向任何处理器发去的消息个数不得超过 [L /g ]个 , 否则便会发生阻塞。 LogP是个异步模型 ,通信与计算可以重叠 , 并完全采用消息传递的方式进行通信和同步。
假设在一个节点中通常有多个加速器,每个加速器都是一个worker,不仅应该考虑节点间的连接,还应该考虑节点内的连接,如PCIe、UPI和NVLink。
论文采用一种拓扑感知模型来预测集体通信操作的延迟。假设链接 l l l在单个方向上的带宽为 W l W_{l} Wl,流量大小为 T l T_{l} Tl。通信的端到端延迟计算如下。并且分别考虑链路两个方向的流量(两个方向流量可能在负载不平衡时差距很大)
L a t c o m m = max l ∈ links { T l W l } L a t_{\mathrm{comm}}=\max _{l \in \operatorname{links}}\left\{\frac{T_{l}}{W_{l}}\right\} Latcomm=l∈linksmax{WlTl}
每条链路上的流量取决于算法和路由策略。在每个边缘上,对不同的操作采用不同的方法来计算流量。
- All-to-all-v 用于将token从序列中的位置路由到它们所需的专家。由于专家选择的灵活性,每对worker之间的流量是高度可变的。我们假设
all-to-all操作只是在所有worker对之间创建链接,并模拟地传输数据。根据拓扑类型的不同,采用一种算法来计算每个工作对之间的路径。对于每对worker,他们之间的流量在路径上的所有有向边上累积。 - All-reduce算子广泛应用于数据同步中,如数据并行度中重复模型参数的梯度,模型并行中嵌入向量等。在每个worker上对一个大小为
S
S
S的张量应用
ring all-reduce,结果是每个worker在管道中总共发送 2 n − 1 n 2\frac{n-1}{n} 2nn−1给它的邻居。 - Broadcast and reduce与
all-reduce一样具有规律性,利用环形连接和流水线来降低其延迟。但与all-reduce不同的是,它们只通过每个链接发送总大小为 S S S的消息。
Note:
DDL-Roofline Model
使用DDL-Roofline Model描述给定集群上特定训练任务的性能。
x轴: R C C R_{CC} RCC
计算和通信是并行MoE模型的两个关键因素。因此,定义计算-通信的比率
R
C
C
R_{CC}
RCC,表示在DDL- Roofline的X轴上,如下所示:
R
C
C
=
L
a
t
c
o
m
p
L
a
t
c
o
m
m
R_{C C}=\frac{L a t_{\mathrm{comp}}}{L a t_{\mathrm{comm}}}
RCC=LatcommLatcomp
L
a
t
c
o
m
p
L a t_{\mathrm{comp}}
Latcomp和
L
a
t
c
o
m
m
L a t_{\mathrm{comm}}
Latcomm分别表示由预测器估计的计算和通信延迟。
R
C
C
R_{CC}
RCC表示任务是受计算限制还是受通信限制。当
R
C
C
R_{CC}
RCC>1时,计算时间占用端到端延迟时间,否则通信占用大部分延迟时间。这个比率表明了应用不同优化的方向。
y轴:平均计算吞吐量
Y轴的变量为
P
ˉ
\bar{P}
Pˉ,表示所有worker的平均计算吞吐量。训练一个MoE MLP层时,计算如下。
P
ˉ
=
12
α
H
2
∑
w
B
w
N
L
a
t
e
2
e
\bar{P}=\frac{12 \alpha H^{2} \sum_{w} B_{w}}{N L a t_{\mathrm{e} 2 \mathrm{e}}}
Pˉ=NLate2e12αH2∑wBw
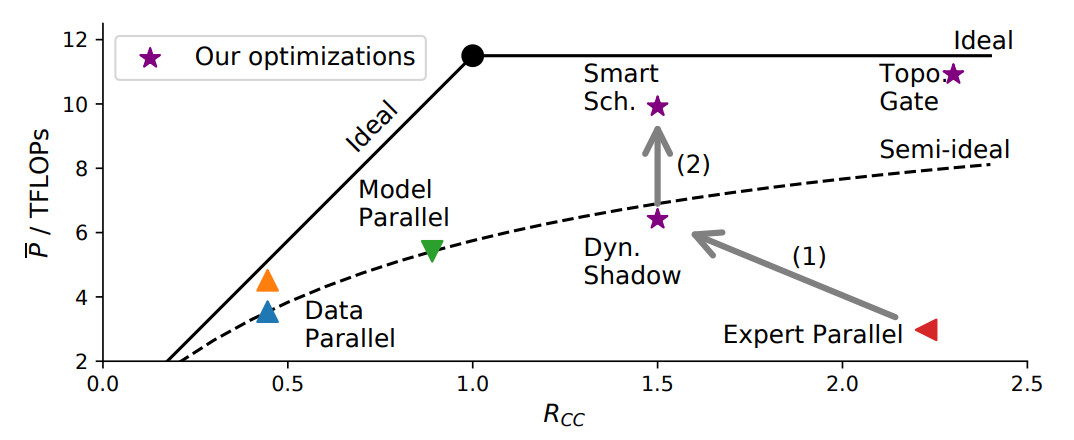
图像综合分析
理想情况下:通信和计算同时进行,得到了一个类似屋顶线的折线,如图5中实线所示的理论上限。计算公式如下:
P
ˉ
ideal
=
P
w
min
{
1
,
R
C
C
}
\bar{P}_{\text {ideal }}=P_{w} \min \left\{1, R_{C C}\right\}
Pˉideal =Pwmin{1,RCC}
半理想情况:以同步方式进行训练时,硬件的充分利用
P
ˉ
semi-ideal
=
P
w
L
a
t
c
o
m
p
L
a
t
c
o
m
p
+
L
a
t
c
o
m
m
=
P
w
R
C
C
R
C
C
+
1
\begin{aligned} \bar{P}_{\text {semi-ideal }} &=P_{w} \frac{L a t_{\mathrm{comp}}}{L a t_{\mathrm{comp}}+L a t_{\mathrm{comm}}} \\ &=P_{w} \frac{R_{C C}}{R_{C C}+1} \end{aligned}
Pˉsemi-ideal =PwLatcomp+LatcommLatcomp=PwRCC+1RCC
在半理想情况下,端到端延迟是通信延迟和计算延迟的总和。最初的roofline模型描述的是在单个设备上的程序,内存访问和计算自然是同时执行的,与此不同的是,分布式训练程序通常需要对系统进行显著的优化,以便同时执行它们。
三、论文提出的解决方案:Model-Guided优化方法
轻量级动态跟踪策略
策略概述
策略驱动:MoE中专家选择可能存在不平衡的情况。传输单个数据的数据量可能比模型参数数量级要小,但是来自所有worker的批量输出可能等于甚至大于模型参数。
权衡点:传输向量的延迟是否可以用传输专家来代替。

如图6所示,一些expert被复制到所有的worker上,即shadow expert,它们的参数,而不是输入token,在网络上传输。它们的相关计算是在本地执行的,直观地减少了包含热门专家的工作人员的负载。
动态shadow的实现
由图4知,expert的popularity随着训练过程的变化而变化,每次迭代可能做的决策不同。此外,参数不能像普通的分布式内存系统那样缓存,因为它们在每次迭代中都要更新,并且需要在更新过程中全局收集梯度。如果它们缓存在每个worker上,那么它们应该在每次迭代中进行更新,从而引入大量的额外开销。即,跟踪有两大瓶颈:
- Expert的popularity随着训练过程的变化而变化,非固定
- 无法简单的进行缓存:参数在迭代中会更新
解决方法预测训练迭代的端到端延迟,以检查性能增益,并据此分析是否应该在运行时跟踪专家。
未使用影子专家前的时延计算
训练MLP层的一次迭代包含1个正向GeMM和2个反向GeMM,用于计算输入的梯度。all-to-all的通信有4轮,包括两次向前传递的all-to-all和两次向后传递的all-to-all。在网络带宽固定的简化情况下,训练时延的计算如下:
L
a
t
i
m
b
l
(
B
)
=
max
w
{
3
4
B
w
α
H
2
P
+
4
B
w
H
W
net
}
L a t_{\mathrm{imbl}}(B)=\max _{w}\left\{3 \frac{4 B_{w} \alpha H^{2}}{P}+4 \frac{B_{w} H}{W_{\text {net }}}\right\}
Latimbl(B)=wmax{3P4BwαH2+4Wnet BwH}
使用影子专家后的时延计算
对于一个shadow专家,必须首先将其参数传播给所有的worker,然后使用获取的模型在本地token上运行计算。在后向阶段,每个worker分别计算其提取的专家的梯度,然后进行all-reduce操作。最后,参数更新操作在最受欢迎的专家最初所在的worker上执行。
在这种情况下,执行不平衡计算的开销被2个集合通信操作符所取代,每个通信操作符的大小为
α
H
2
\alpha H^2
αH2。由于多个受欢迎的专家被派往许多其他工作人员,负载不平衡的情况不太可能发生。投影
r
r
r模型的延迟计算如下:
L
a
t
shadow
(
r
,
B
′
)
=
max
w
{
3
4
B
w
′
α
H
2
P
}
+
2
r
2
α
H
2
W
net
L a t_{\text {shadow }}\left(r, B^{\prime}\right)=\max _{w}\left\{3 \frac{4 B_{w}^{\prime} \alpha H^{2}}{P}\right\}+2 r \frac{2 \alpha H^{2}}{W_{\text {net }}}
Latshadow (r,B′)=wmax{3P4Bw′αH2}+2rWnet 2αH2
其中
B'表示修改后的批次大小。
权衡结果总结
推导后,进行模型交换而非数据交换的条件为:
-
传输输入的总开销高于传输模型
B max > r α H B_{\max }>r \alpha H Bmax>rαH -
减少的计算延迟大于增加的通信开销
3 ( B max − B max ′ ) α H r α H − B max > P W net \frac{3\left(B_{\max }-B_{\max }^{\prime}\right) \alpha H}{r \alpha H-B_{\max }}>\frac{P}{W_{\text {net }}} rαH−Bmax3(Bmax−Bmax′)αH>Wnet P
在这两种情况下,都启用了动态阴影来减少端到端延迟。否则,通信开销太大,而且模型交换不能为减少延迟带来好处,因此不能执行。这种情况通常发生在不同worker的工作量平衡时。图5中的箭头(1)表示,由于减少了空转,计算的延迟缩短了,导致了更低的 R C C R_{CC} RCC和更高的 P ^ \hat{P} P^.
算法实现[贪心]
在每个迭代的运行时选择专家进行跟踪。在每个worker上执行一个轻量级算法,如算法1所示。根据上面的公式,它返回一组需要对其进行跟踪的专家。

Note:核心还是一种贪心的思想
异步细粒度智能调度
细粒度任务的划分
问题:当通信和计算分开执行时,程序不能超出半理想曲线。
解决方案:将任务划分为更小的部分,并重新调度细粒度的通信和计算操作,以提高效率。细粒度调度允许计算和通信异步执行,从而更好地利用硬件,使其能够超越图5中箭头(2)所示的半理想曲线。

划分通信:专家并行中,通信遵循all-to-all的模式,使用启发式算法将worker划分更细粒度的组,分割所有人的通信。使用分组的pairwise交换算法去执行all-to-all。
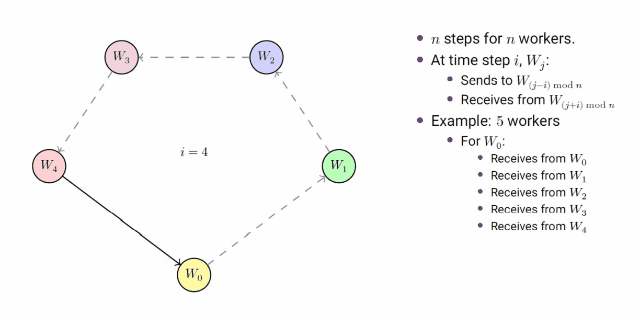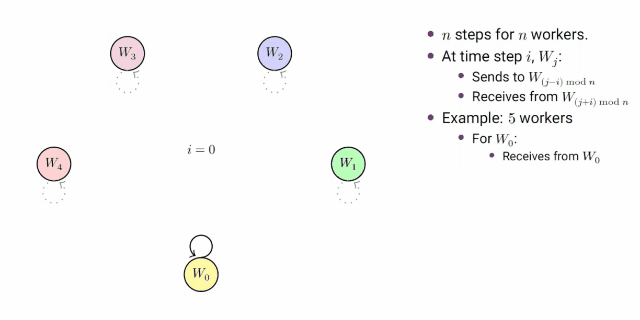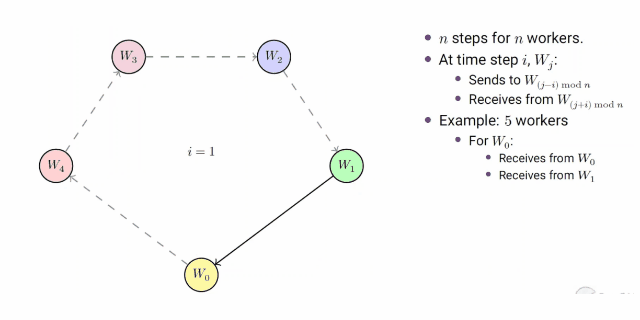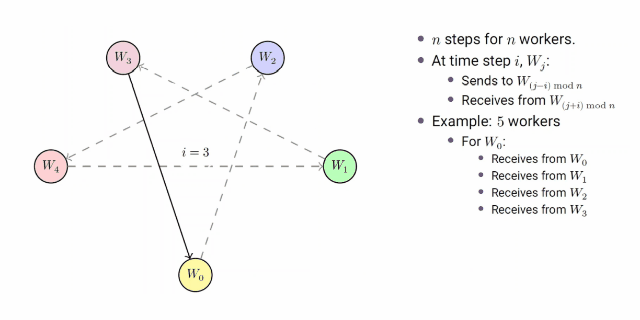
分组划分与环形通信
**group pair-wise算法:**n个由worker构成的组组成一个大小为n的环,以0到n-1递增的步长向其他的组发送数据。第k步的发送步骤如下描述:
- 在
s
t
e
p
i
step_i
stepi时:
- w j w_j wj向 w j − i w_{j-i} wj−i发送数据
- w j w_j wj从 w j + i w_{j+i} wj+i接收数据
**具有依赖关系的计算和通信的进行:**在一个MoE层的前向或后向阶段,涉及两个对称的all-to-all,并在它们之间进行计算。按照两两交换的方式分割计算,为重新组织它们留出空间。3n个操作由n个组中的所有worker分n个步骤执行。在步骤j中,组i中的worker执行以下3个操作,由图7中的示例实例化。
- S i , j S_{i,j} Si,j:发送到组 t i , j = ( i − j ) t_{i, j}=(i-j) ti,j=(i−j)并从 f i , j = ( i + j ) f_{i, j}=(i+j) fi,j=(i+j)接收token(都对n取模)。
- C i , j C_{i,j} Ci,j:使用本地专家从 f i , j f_{i,j} fi,j,在token上进行计算。
- R i , j R_{i,j} Ri,j:从 t i , j t_{i,j} ti,j接收本地 token 的输出并把计算结果送回到 f i , j f_{i,j} fi,j

调度的目标是并行地执行计算和通信。为每个worker创建一个通信流和一个计算流,以执行不同类型的操作符。但所有操作都必须遵循它们的数据依赖关系,并在启动自己之前等待之前的任务执行。
Note:数据依赖关系可以由下图表示

不同的遵循数据依赖关系的调度方式如下:
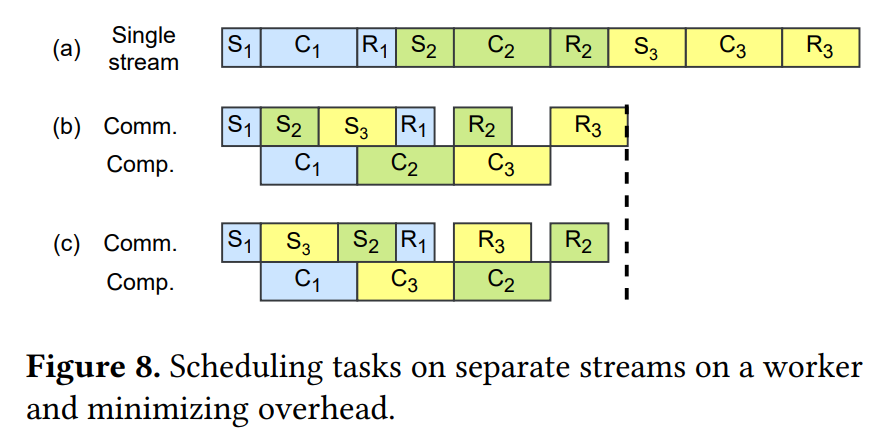
可以看出,在计算流始终繁忙的情况下如图8(b),©,能够优化时间的主要机会是第一个S和最后一个R。pairwise调度能保证对于任何一个worker来说,最快的两个操作 S i , 0 S_{i,0} Si,0为第一个, R i , n − 1 R_{i,n-1} Ri,n−1为最后一个,最大限度的减少开销。
避免竞争的专家选择策略
MoE模型中,最终目标是用足够多的样本来训练专家,而不是每个样本都被期望的专家处理。并且由于采用拟合分数作为权重,改变专家的选择并不会造成数值上的错误。如[前文](#网络拥塞与竞争(severe network contention))所述,在树形结构的普通集群中,上层连接的带宽通常低于本地连接。与其他常规的集体交流不同,all-to-all 会导致链路上更高的竞争。因此可以通过限制通过上层链接的token数量减少上层连接的竞争压力。限制的具体方法:
假设交换机连接 N 个节点和每个节点上的M 个 workers。worker和主机之间的流量大致为 T w = M N − 1 M N B H T_{w}=\frac{M N-1}{M N} B H Tw=MNMN−1BH。同时,每个节点网口的流量为 T n = M ( N − 1 ) N B H T_{n}=\frac{M(N-1)}{N} B H Tn=NM(N−1)BH,大约比 T w T_w Tw大M倍。
为了减少拥塞,允许将最多 L = W net M W local B L=\frac{W_{\text {net }}}{M W_{\text {local }}} B L=MWlocal Wnet B 个token定向到另一个节点。这里, W n e t W_{net} Wnet和 W l o c a l W_{local} Wlocal分别表示节点间和节点内的通信带宽。具体来说,如果有超过L个token,其最佳选择位于另一个节点上,则允许其中得分最高的L个token。它们的其余部分与其他token一起留在本地节点中重新选择它们所需的专家。
四、实验和评估
实验设置
FastMoE:实验是基于FastMoE,FastMoE是全球首个基于PyThorch的可以专家并行训练网络的框架。实验实现时修改了其中的某些操作,添加了若干的门网络验证实验。
Megatron- L M 6 LM^6 LM6:训练Transformer的框架
实验比较对象
和若干不同的系统进行了相关比较:
支持k个专家选择的baseline
- 未优化的FastMoE:专家并行baseline
- DeepSpeed+ZeRO:数据并行baseline
- MoE
使用专家选择修改达到优化的baseline
-
GShard:state-of-art MoE系统(by Google)
限制了每个专家的能力(输入数量),达到负载均衡的情况。去掉多余的输入。
-
FairSeq+BASE Layers:另一个state-of-art MoE系统(by Facebook)
使用匹配算法,在完美的负载均衡的情况下提升分数总和。
硬件和实验模型
硬件:
- johnny cluster:16 NVIDIA V100 PCIe GPUs in 2 nodes
- trevor cluster:64 NVIDIA V100 PCIe GPUs in 16 nodes
模型:
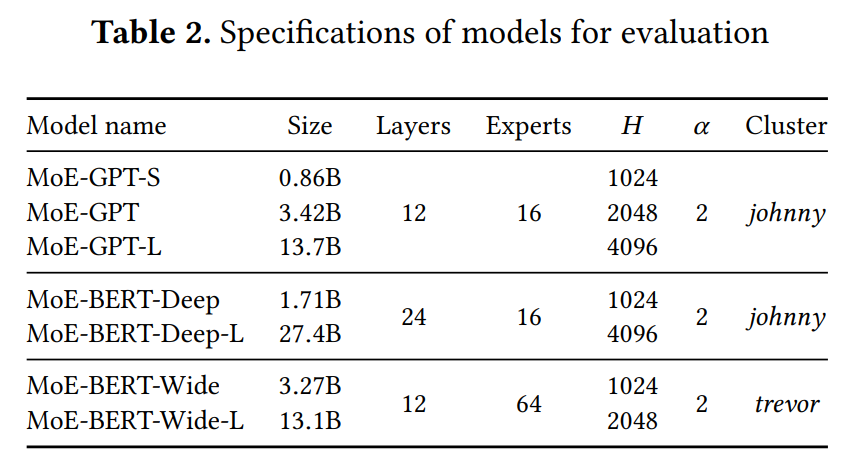
实验结果
第一组baseline下的实验结果
比较训练单个MoE层的加速:

- More than 17x speedup over DeepSpeed + ZeRO baseline.
- More than 5x speedup over FastMoE baseline.
第二组baseline下的实验结果
因为修改了模型本身的行为,对比了收敛的速度:

- Both baseline systems take significantly more steps to converge.
- Convergence speed is 1.37x shorter than GShard, and 2.19x shorter than BASE Layers.
- The topology-aware gate makes iterations 9. 4% faster.
评估总结
-
背景:MoE模型较大且具有动态性
-
在分布式环境下训练MoE提出了三个策略解决三个问题:
-
解决专家选择倾斜的问题:影子专家
-
解决粗粒度计算:计算和通信重叠
-
解决信道竞争:门网络减少拥塞
-
-
提出DDL-roofline可以评估系统的性能。
-
实验:与大型模型的最先进系统(包括ZeRO、GShard和基础层)设计实验比较,FasterMoE实现了1.37 - 17.87的加速。

























 1065
1065

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










