机器学习——异常检测与主成分分析

最新推荐文章于 2024-01-01 12:33:31 发布

谷雨白

最新推荐文章于 2024-01-01 12:33:31 发布

阅读量1.7k

点赞数 1

分类专栏：笔记文章标签：机器学习 python pca降维

本文链接：https://blog.youkuaiyun.com/weixin_45739665/article/details/114501782

版权

一、异常检测

1.1可以用到的案例

欺诈检测：盗刷信用卡检测
入侵检测：检测网络入侵或计算机入侵行为
医疗：缺陷基因检测
生态系统：预测飓风、洪水、干旱、热浪和火灾的发生

1.2监督式异常检测

提前使用带“正常”与“异常”标签的数据对模型进行训练，机器基于训练好的模型判断新数据是否为异常数据

1.3无监督式异常检测

通过寻找与其他数据最不匹配的实例来检测出未标记测试数据的异常

1.4定义

基于数据分布，寻找与其他数据最不匹配的实例
寻找发生可能性比较低的事件

二、概率密度函数

在连续分布事件中，用于描述连续随机变量的输出值在某个确定的取值点附近的可能性的函数，通过其可计算取值点附近区间发生事件的概率

2.1基于高斯分布的概率密度函数

现实生活中，很多事件发生的频率都符合高斯分布，比如：工业产品的强力、抗压强度、口径、长度等指标；人体的身高、体重等指标；同一品种种子的重量；某个地区的年降水量，等等

2.2基于高斯分布概率密度函数实现异常检测

在这里插入图片描述

u1 = x1_mean
u2 = x2_mean
sigma1 = x1_sigma
sigma2 = x2_sigma

p1 = 1/sigma1/math.sqrt(2*math.pi)*np.exp(-np.power((x1-u1),2)/2/math.pow(sigma1,2))

在这里插入图片描述

三、数据降维

3.1问题

想建立一个AI模型，筛选金融股票，潜在数据指标：价格、交易量、换手率、股东人数、最近N日涨跌幅、RSI指标、市值、营业额、净利润、负债率、利润增长率…多达几百\上千个因子
两大问题：求解困难、模型过拟合

3.2定义

在一定的限定条件下，按照一定的规则，尽可能保留原始数据集重要信息的同时，降低数据集特征的个数

3.3为什么需要数据降维

维数灾难：随着特征数量越来越多，为了避免过拟合，对样本数量的需求会以指数速度增长
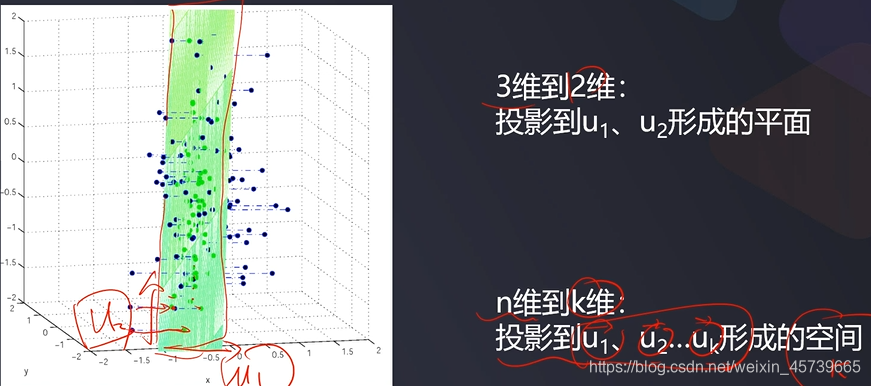
数据可视化：高维数据不能可视化，只有降低到二维或三维才能可视化
3D数据降维到2D数据

在这里插入图片描述

四、数据降维最常用的方法——主成分分析（PCA）

也称主分量分析，按照一定规则把数据变换到一个新的坐标系统中，使得任何数据投影后尽可能可以分开（新数据尽可能不相关，分布方差最大化）。
核心：投影后的数据尽可能分得开（即不相关）

4.1PCA的实现

使投影后数据得方差最大，因为方差越大数据也越分散
数据预处理（数据分布标准化：μ=0，α=1）
计算协方差矩阵特征向量、及数据在各特征向量投影后的方差
根据需求（任务指定或方差比例）确定降维维度K
选取K维特征向量，计算数据在其形成空间得投影

#数据标准化处理,均值变为0，标准差变为1
from sklearn.preprocessing import StandardScaler
X_norm=StandardScaler().fit_transform(X)
print(X_norm)

##数据降维到2维
from sklearn.decomposition import PCA
pca=PCA(n_components=2)
X_pca=pca.fit_transform(X_norm)
print(X_pca.shape,X_norm.shape)
#计算方差比例
var_ratio2=pca.explained_variance_ratio_
print(var_ratio2)

五、任务

5.1任务一：异常消费行为检测：基于数据，基于高斯分布得概率密度函数实现异常消费行为检测

可视化消费数据、数据分布次数、及其对应高斯分布得概率密度函数
设置概率密度阈值0.03，建立模型，实现异常数据点预测
可视化异常检测处理结果
修改概率密度为0.1、0.2，查看阈值改变对结果得影响
修改概率密度阈值为0-0.2，以0.01为递增间隔，查看保存结果、生成动态gif图

# In[]
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np

data=pd.read_csv('PCA_AnomalyPay.csv')

import matplotlib as mpl
mpl.rcParams['font.family']='SimHei'

# In[]
fig1=plt.figure(figsize=(8,6))
plt.scatter(data.loc[:,'frequency'],data.loc[:,'payment'],marker='x')
plt.title('原始数据')
plt.xlabel('频率')
plt.ylabel('消费')
plt.show()

在这里插入图片描述


x1=data.loc[:,'frequency']
x2=data.loc[:,'payment']

# In[]
#数据分布的可视化操作
fig2=plt.figure(figsize=(20,5))
fig2_1=plt.subplot(121)
plt.hist(x1,bins=100)   #频次图，bins划分成多少块
plt.title(