目录
首先介绍两本重要的书籍:
- Boyd, S., Boyd, S. P., & Vandenberghe, L. (2004). Convex optimization. Cambridge university press.
- Deb, K. (2012). Optimization for engineering design: Algorithms and examples. PHI Learning Pvt. Ltd..
- Sioshansi, R., & Conejo, A. J. (2017). Optimization in Engineering. Cham: Springer International Publishing, 120.【下载链接】
1. KKT条件与算例
1.1 理论推导
给定如下一个标准的优化问题模型:

可以构造如下拉格朗日函数:
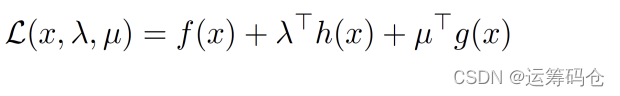
KKT条件包含三个部分:
- 原始变量的导数,这是一组约束,你有几个原始变量就会有几个灯饰
- 原来的等式约束、不等式约束
- 等式约束的拉格朗日乘子符号是自由的,小于等于不等式约束的乘子符号为正,大于等于的为负
针对上述模型,其对应的KKT条件为:
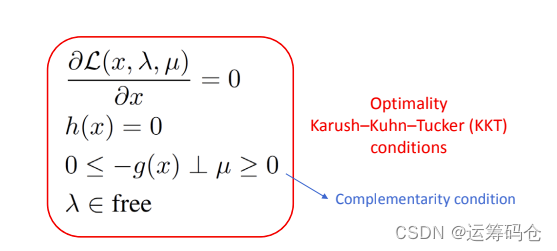
我们求解了上述方程组,也就意味着我们得到原始优化问题的解。
1.2 一个计算案例

注意:
- 每个约束会对应一个对偶变量,所以我们有6个约束,就对应着6个对偶变量。
- 由于所有约束都是大于等于不等式,所以其对应的对偶变量都是非正的;为了遵从惯例,我们将对偶变量前的符号统一设置为减号,就回到传统的非负的表达习惯上了。
为此,我们推导出的KKT条件如下:

我们能不能以更紧凑的形式来表述KKT条件呢?答案是,当然可以。就是把所有KKT条件都写成互补松弛约束,结果如下:

那么,我们如何得到上述方程组的解呢?上述问题是一个互补松弛问题(mixed complementary problem),没有目标函数函数;求解的方法有以下几个:
- PATH求解器:链接
- 非线性求解器:目标为 minimize 1;约束集为 互补松弛条件。
- 我们还可以通过引入0-1辅助变量对互补松弛条件进行线性化。
2 如何生成一个对偶问题
2.1 对偶函数
首先,为什么我们要生成一个对偶问题呢?因为它可以为我们要找到一个下界。
如果满足原问题是凸优化问题,并且至少存在绝对一个绝对可行点(什么叫绝对可行点,就是一个可以让所有不等式约束都不取等号的可行点),那么就具有强对偶性。这个条件就是传说中的Slater’s condition。

注解:
- 对偶函数是一个无约束优化问题,任意给定的对偶变量,对偶函数的目的都是最小化(松弛)拉格朗日函数。因此,在对偶函数中,决策变量只有x,而
是任意值。。
- 为什么是松弛拉格朗日函数呢?因为原问题的约束被松弛掉了,固定变量被用来对这种松弛进行惩罚。
- 对偶函数的最优值提供了原始问题的一个下界。
2.2 最优下界
我们希望得到的自然是最好的下界,这时候我们的决策变量就变成了。于是有:

对照刚才举的例子:
 在这个问题中,套娃出现了。我们先给一个
在这个问题中,套娃出现了。我们先给一个 然后,再得到其对应的x。问题成了两层,我们不希望这样,那咋办呢?替换变量呀。
2.3 KKT转化
我们可以使用KKT条件来替换上述minimize的部分,只保留maximize部分,不就可以。但是还得注意:
- 最小化部分,优化的是x,因此
是一个常数,但这个常数又是外边最大化部分的决策变量
- KKT条件转化过程中,常数部分保持不变,保留在目标函数中;其余部分转移到约束中去
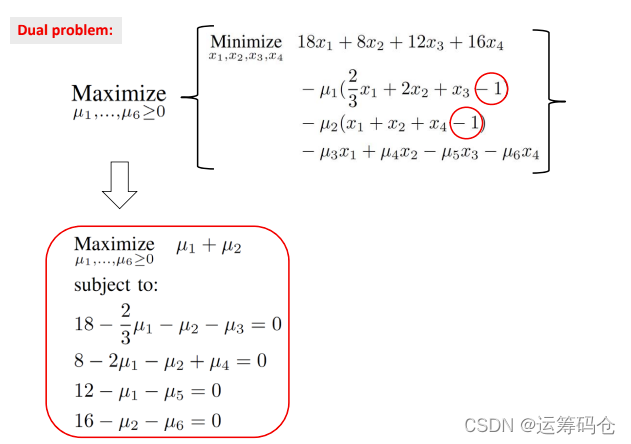
注解:
- 为啥没有x了呢?因为是线性问题,求导的时候就只剩下x的系数了。
2.4 更紧凑的对偶模型
我们都知道,所有的对偶变量都是非负的;观察对偶问题的目标函数,发现 在目标函数中并没有出现;那么,他存在在约束中也就没什么意义了。移除他们,将等式约束转化成不等式约束,得到的问题就是等价的了。于是有:
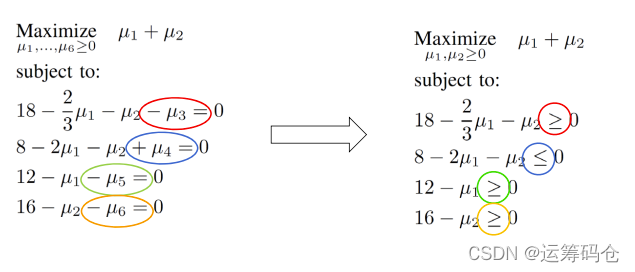
总结两种转换方法如下:

2.5 强对偶和弱对偶
弱对偶:

强对偶:
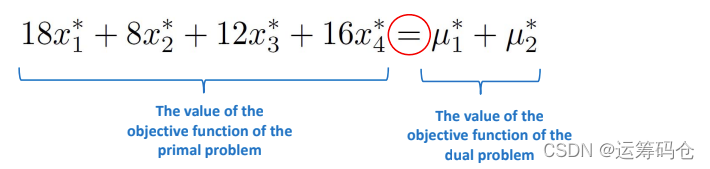
2.6 总结
- 原问题的变量数目等于对偶问题的约束数目
- 原问题的约束数目等于对偶问题的变量数目
- 对偶问题的对偶问题是原问题
- 对偶问题的对偶变量是原变量
- 弱对偶:在可行域内,对偶问题的可行解 小于等于 原问题的可行解
- 强对偶:Slater’s condition成立,对偶问题的最优值等于原问题的最优值。








 本文深入探讨了Karush-Kuhn-Tucker(KKT)条件在优化问题中的应用,通过理论推导和实例解析展示了如何利用KKT条件解决约束优化问题。同时,介绍了如何构建对偶问题,讨论了强对偶和弱对偶的概念,以及它们与原始问题的关系。通过对一个具体的优化案例的分析,阐述了如何将KKT条件转化为互补松弛问题并求解。此外,还讨论了对偶问题在提供原问题下界方面的价值,以及Slater's条件在确保强对偶性中的作用。
本文深入探讨了Karush-Kuhn-Tucker(KKT)条件在优化问题中的应用,通过理论推导和实例解析展示了如何利用KKT条件解决约束优化问题。同时,介绍了如何构建对偶问题,讨论了强对偶和弱对偶的概念,以及它们与原始问题的关系。通过对一个具体的优化案例的分析,阐述了如何将KKT条件转化为互补松弛问题并求解。此外,还讨论了对偶问题在提供原问题下界方面的价值,以及Slater's条件在确保强对偶性中的作用。


















 1042
1042

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










