Python基础_02进制以及原码、反码和补码

---

1 进制

1.1 进制介绍

计算机世界中只有二进制，所以计算机中存储和运算的所有数据都要转为二进制。包括数字、字符、图片、声音、视频等。常见的进制：
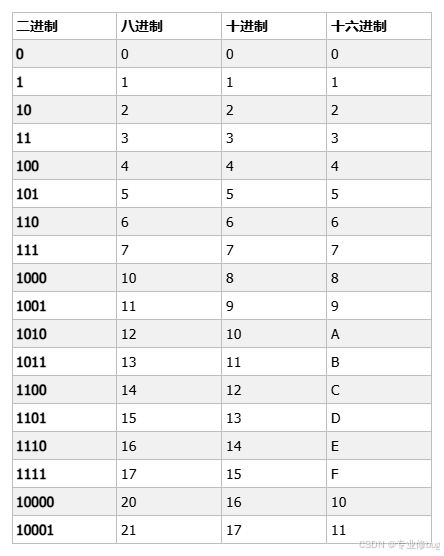
（1）二进制：0、1，满2进1。
（2）八进制：0-7，满8进1。
（3）十进制：0-9，满10进1。
（4）十六进制：0 - 9及A-F，满16进1。十六进制中，除了 0 到 9 十个数字外，还引入了字母，以便表示超过9的值。字母A对应十进制的10，字母B对应十进制的11，字母 C、D、E、F 分别对应十进制的 12、13、14、15。

1.2 不同进制表示整数的方式

（1）二进制：以0b或0B开头表示。
（2）八进制：以0o开头表示
（3）十进制：正常数字表示。
（4）十六进制：以0x或0X开头表示，此处的A-F不区分大小写。

# 十进制
dec = 10
# 二进制：以Ob开头
binary_num = 0b1010
# 八进制：以0o开头
octal_num = 0o12
# 十六进制：以0x或0X开头
hex_num1 = 0XA
hex_num2 = 0xA
print(dec)  # 10
print(binary_num)  # 10
print(octal_num)  # 10
print(hex_num1)  # 10
print(hex_num2)  # 10

# 进制间的转换
print("=================")
print("十进制数为：", dec)  # 10
print("转换为二进制为：", bin(dec))  # 0b1010
print("转换为八进制为：", oct(dec))  # 0o12
print("转换为十六进制为：", hex(dec))  # 0xa

1.3 二进制、八进制、十六进制转换成十进制

1. 二进制转换成十进制

（1）规则：从最低位开始，将每个位上的数提取出来，乘以2的（位数-1）次方，然后求和。
（2）案例：请将二进制 1011 转成十进制的数。

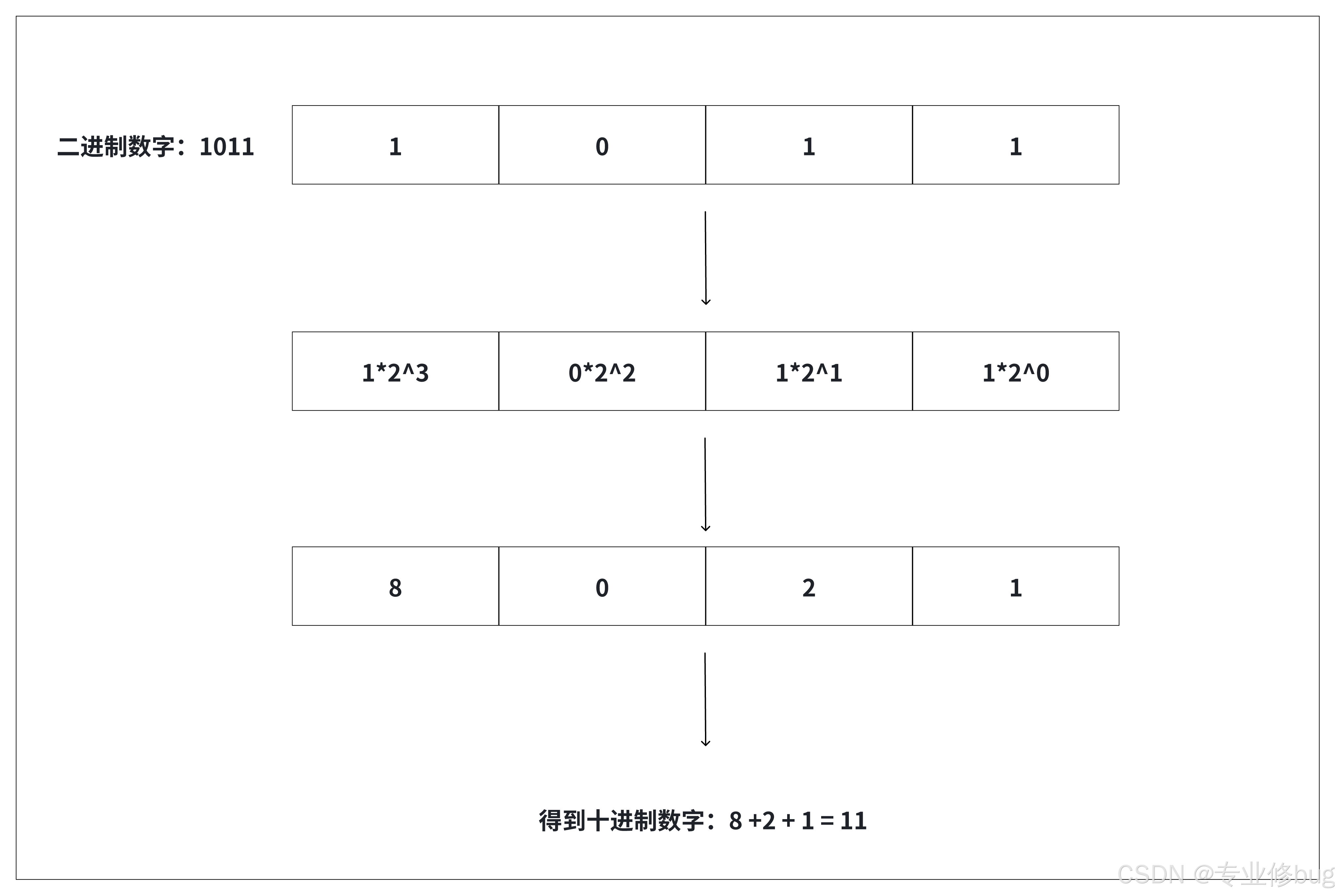
2. 八进制转换成十进制

（1）规则：从最低位开始，将每个位上的数提取出来，乘以8的（位数-1）次方，然后求和。
（2）案例：请将0o231转成十进制的数。

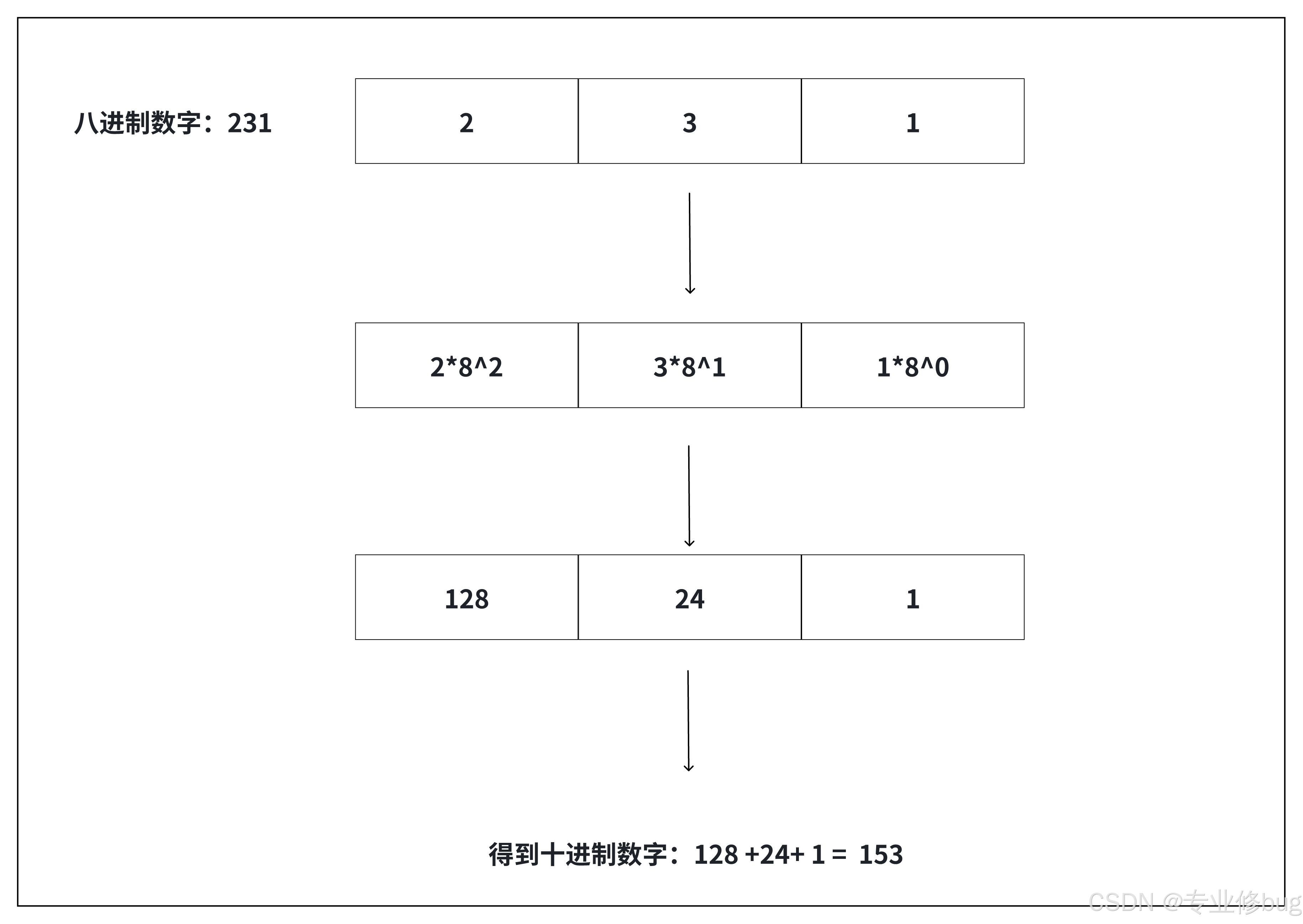
3. 十六进制转换成十进制

（1）规则：从最低位开始，将每个位上的数提取出来，乘以16的（位数-1）次方，然后求和。
（2）案例：请将0x34A转成十进制的数。

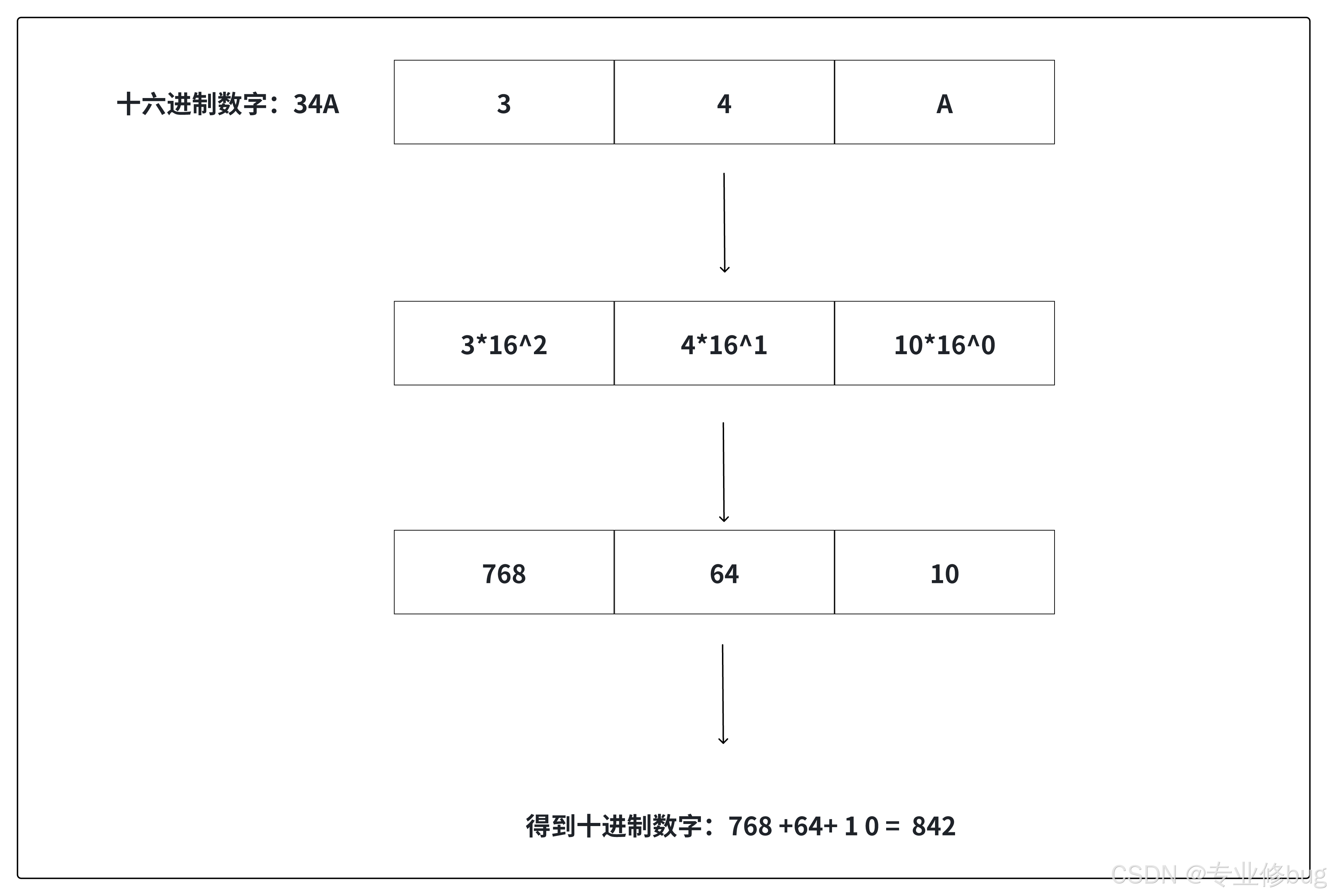
1.4 十进制转换成二进制、八进制、十六进制

1. 十进制转换成二进制

（1）规则：将该数不断除以2，直到商为0为止，然后将每步得到的余数倒过来，就是对应的二进制。
（2）案例：请将 56 转成二进制。

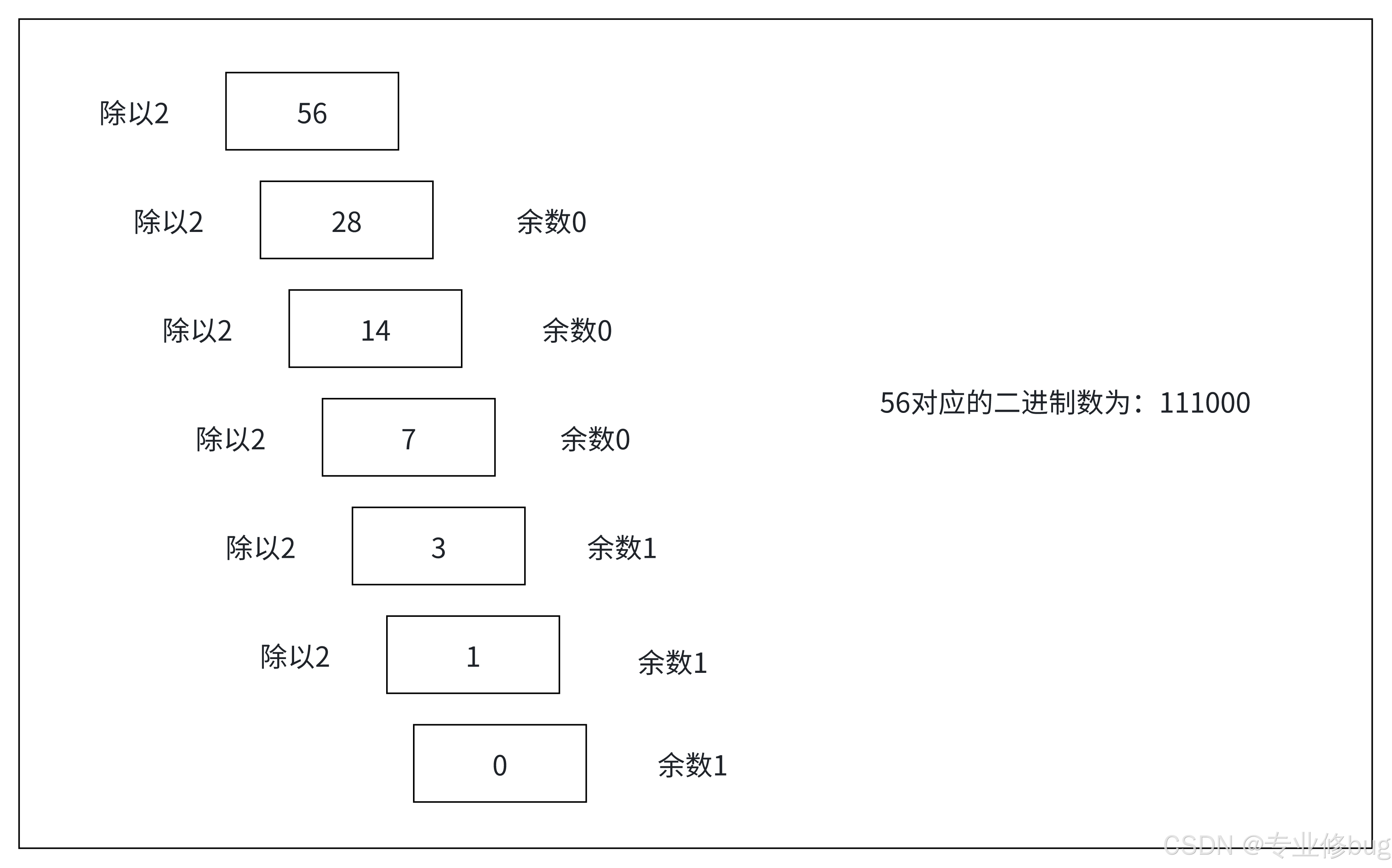
2. 十进制转换成八进制

（1）规则：将该数不断除以8，直到商为0为止，然后将每步得到的余数倒过来，就是对应的八进制。
（2）案例：请将356转成八进制。

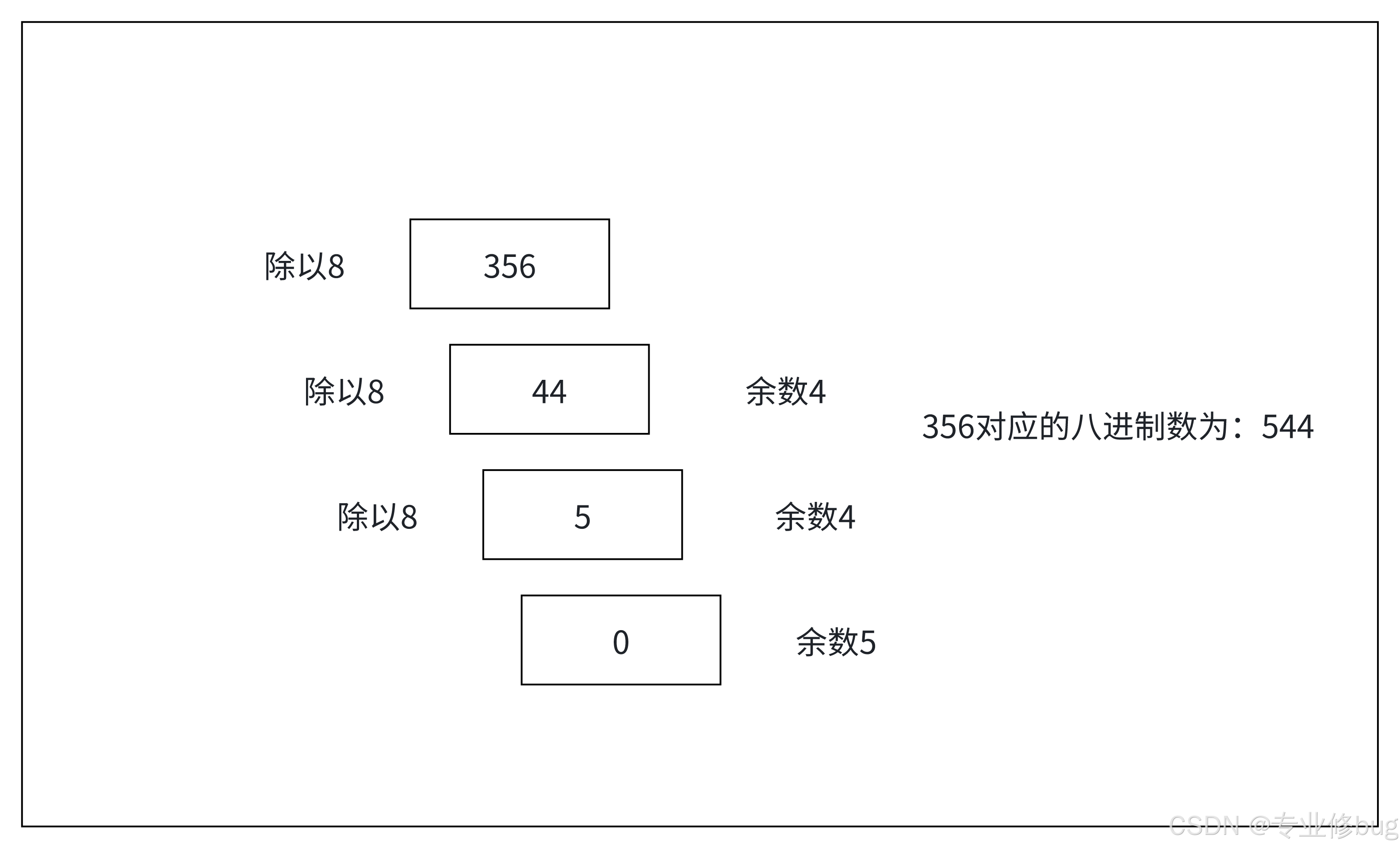
3. 十进制转换成十六进制

（1）规则：将该数不断除以16，直到商为0为止，然后将每步得到的余数倒过来，就是对应的十六进制。
（2）案例：请将356转成十六进制。

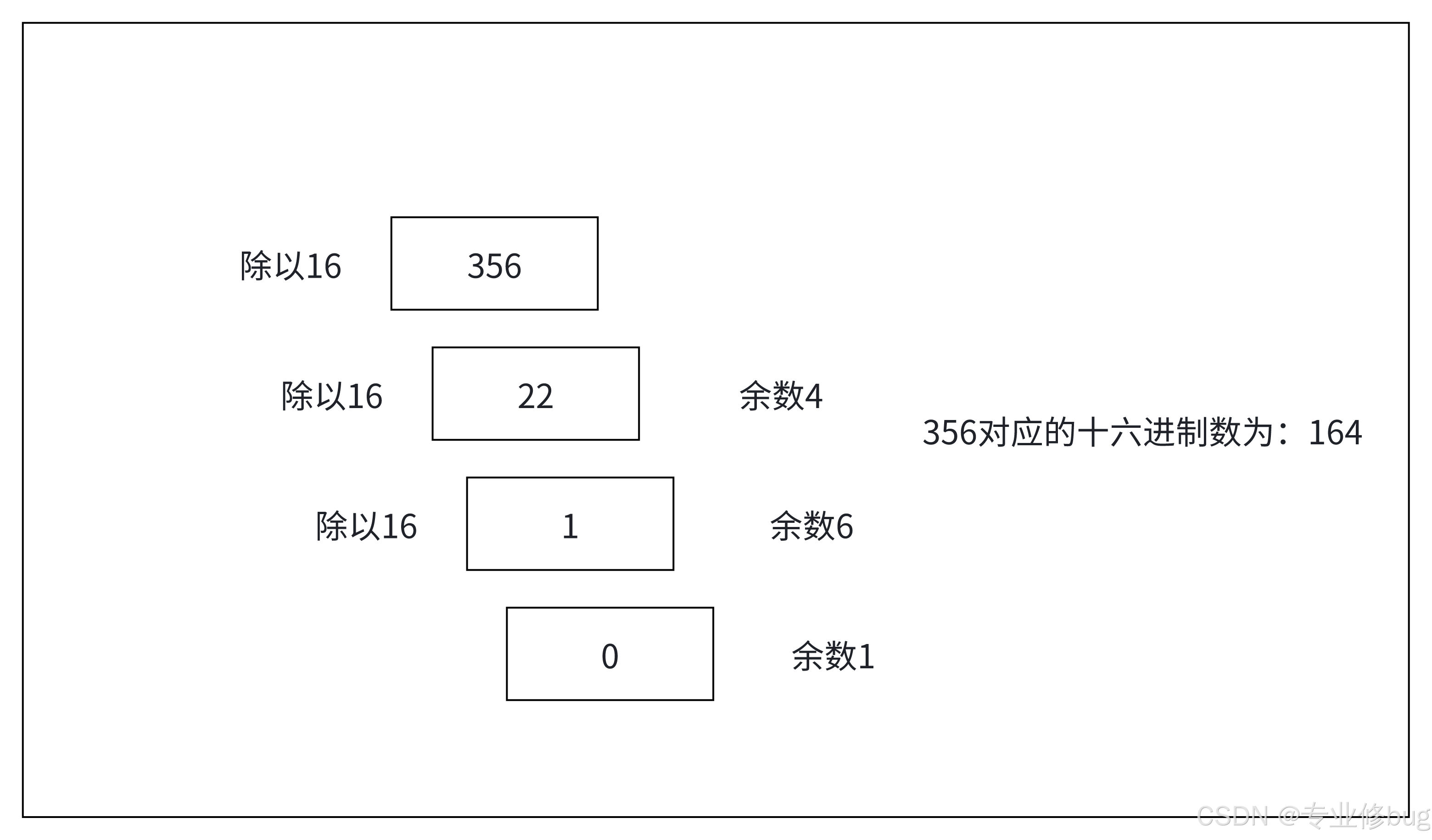
1.5 二进制转换为十六进制、八进制

1. 二进制转换为十六进制

（1）规则：低位开始，将二进制数每四位一组，转成对应的十六进制数即可。
因为2的4次方等于16 ，所以将二进制数从右向左每 4 位分成一组。如果二进制数的位数不是 4 的倍数，则在最左边补零，使其成为 4 的倍数
（2）案例：请将1001011转成十六进制。

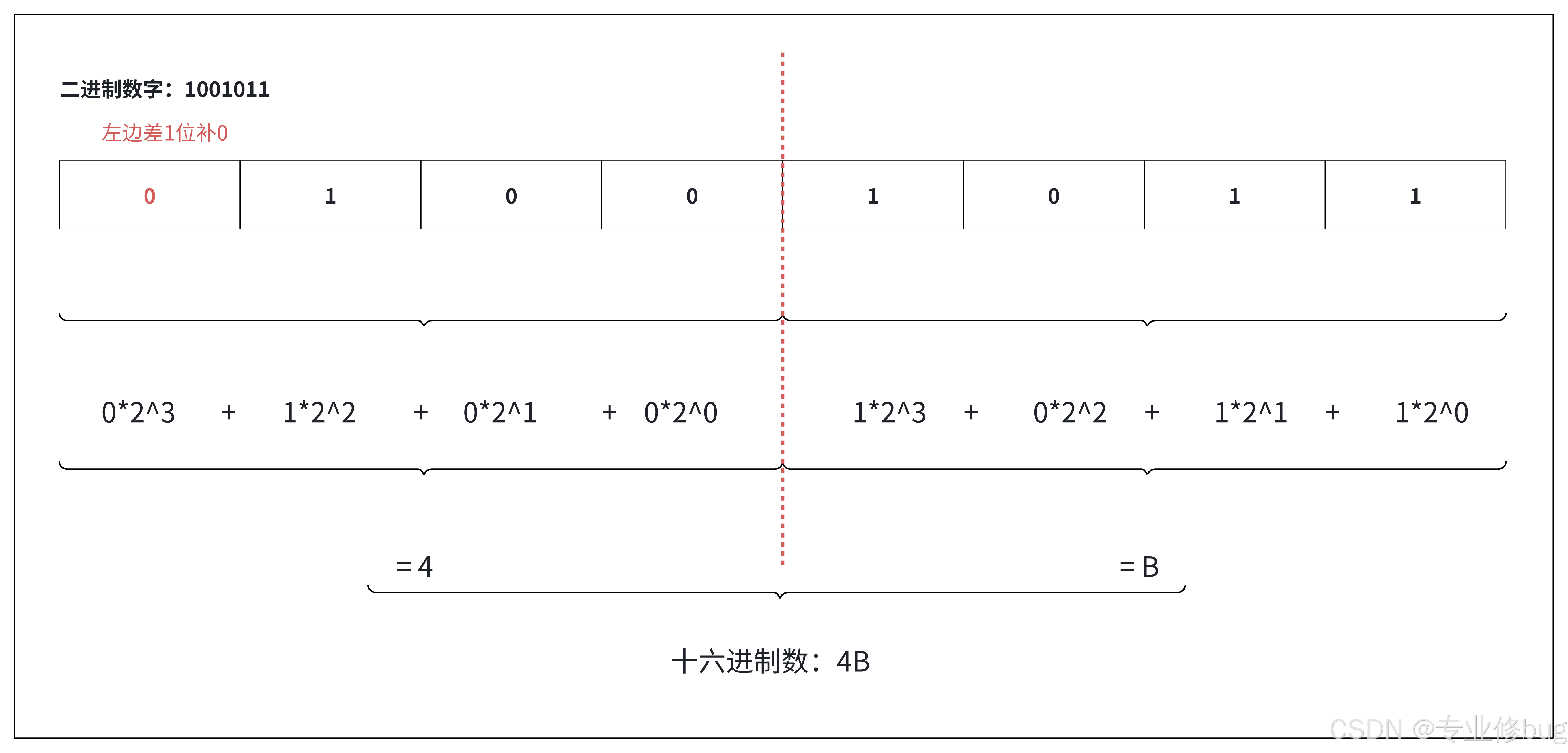
2. 二进制转换为八进制

（1）规则：低位开始，将二进制数每3位一组，转成对应的八进制数即可。
因为2的3次方等于8 ，所以将二进制数从右向左每 3 位分成一组。如果二进制数的位数不是 3 的倍数，则在最左边补零，使其成为 3 的倍数
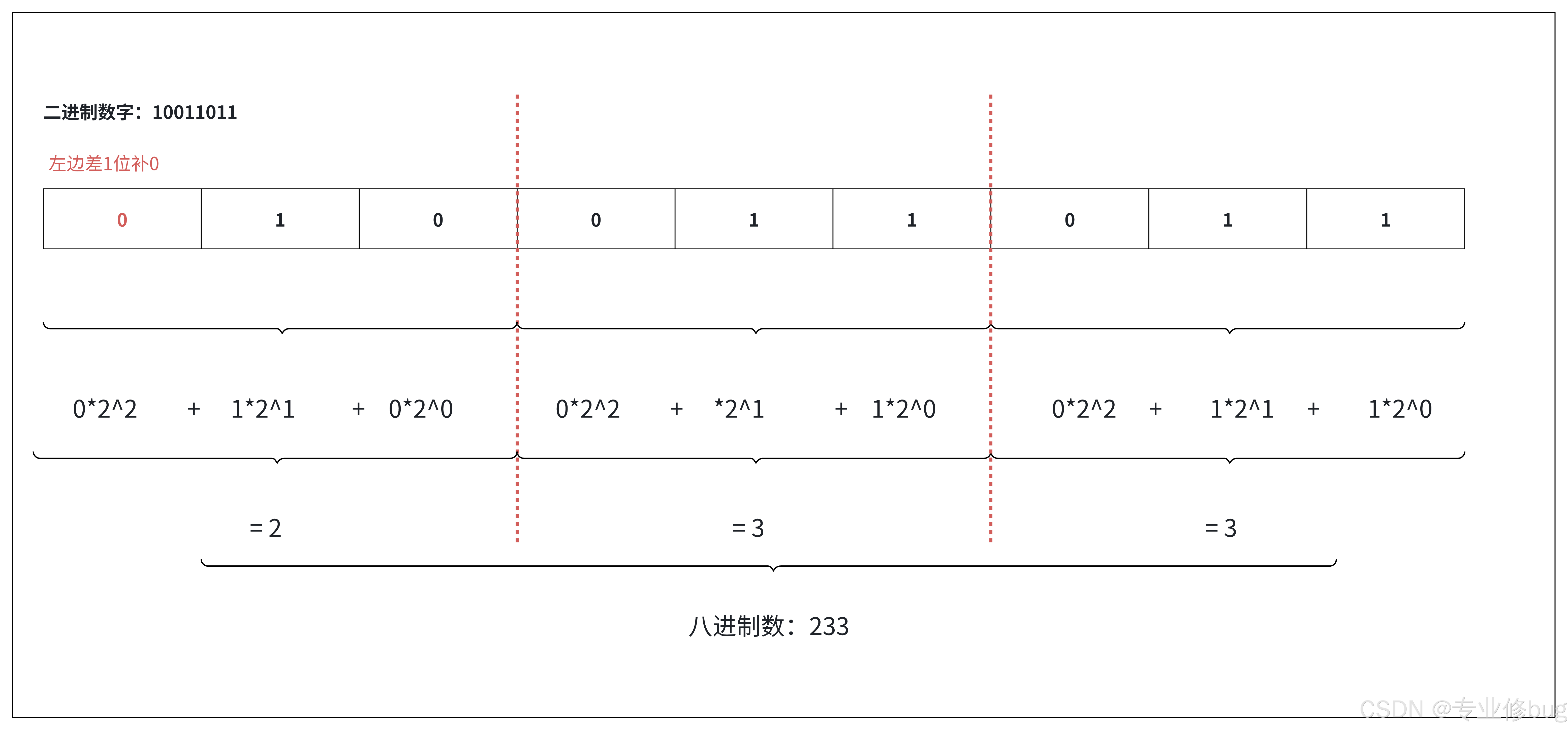
（2）案例：请将10011011转成八进制。

1.6 八进制、十六进制转为二进制

1. 八进制转为二进制

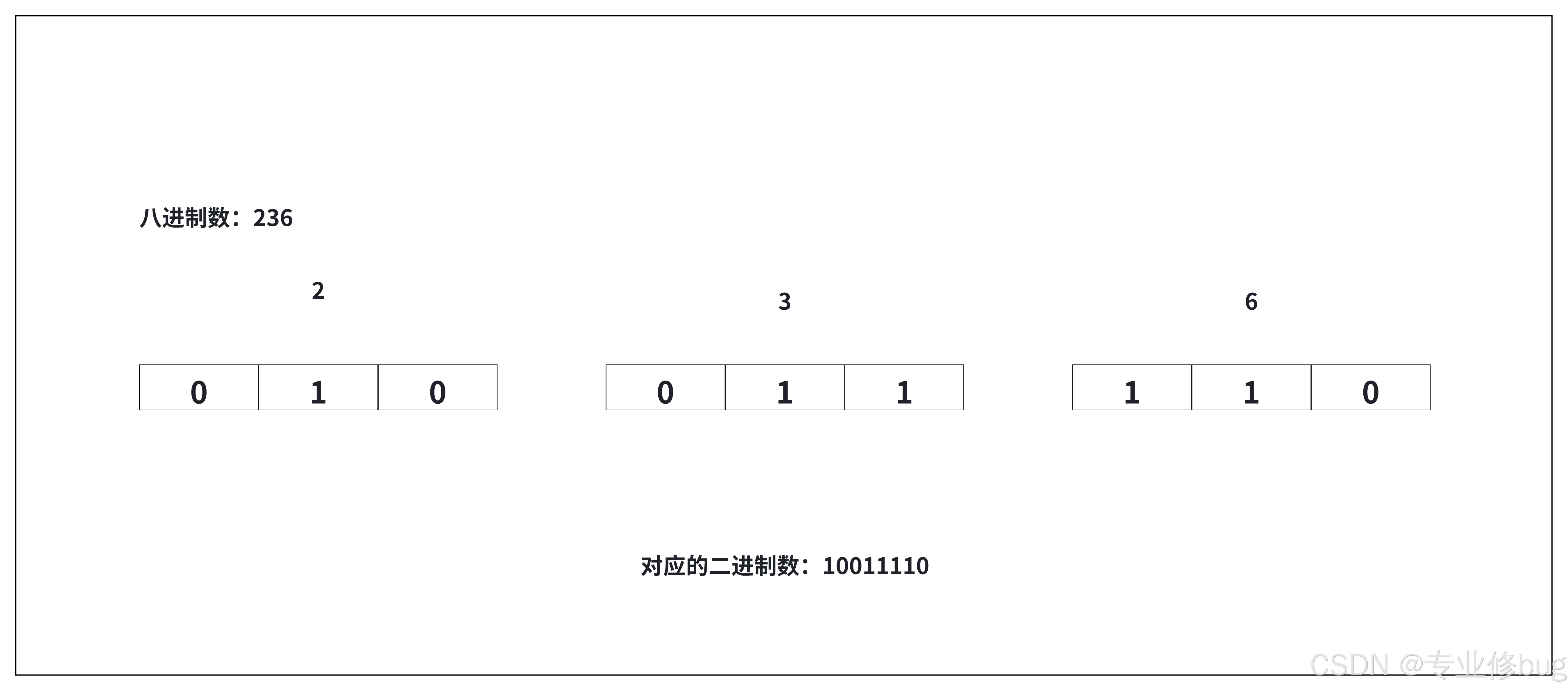
（1）规则：将八进制数每1位，转成对应的3位的一个二进制数即可。
（2）案例：请将0o236转成二进制。

2. 十六进制转为二进制

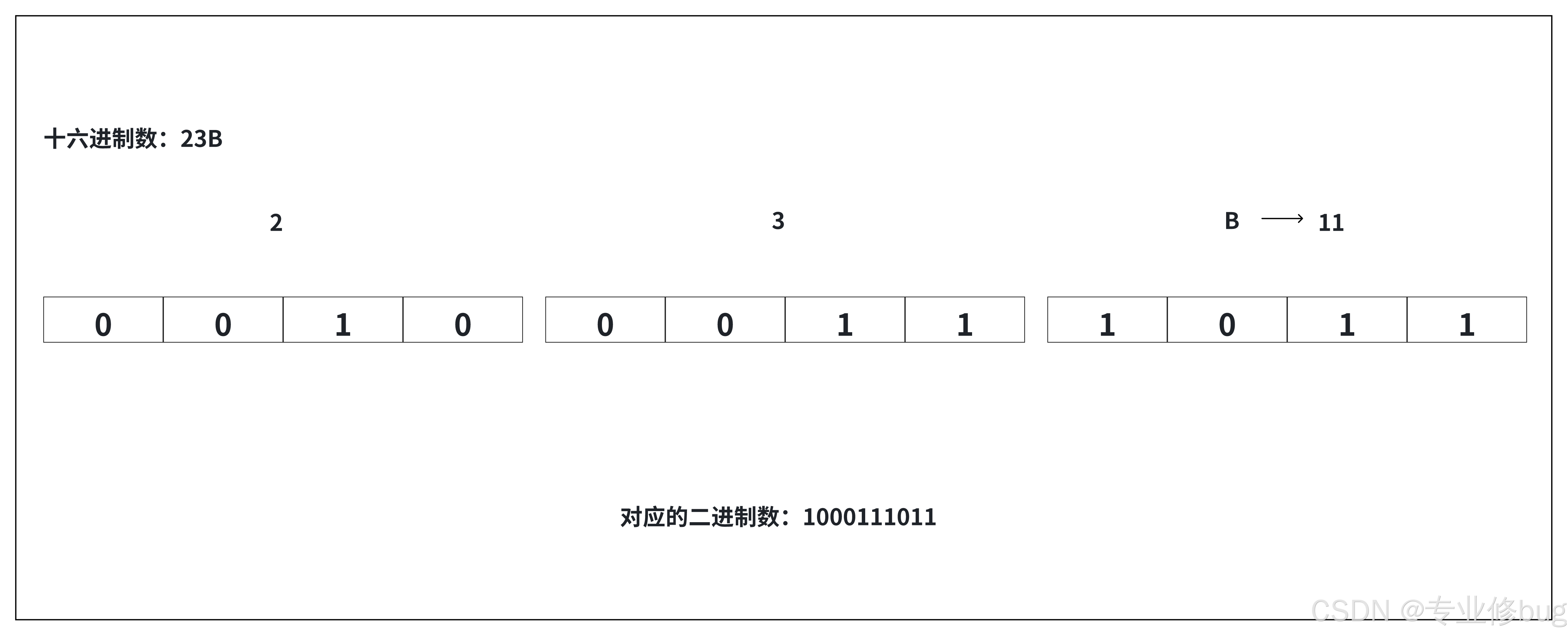
（1）规则：将十六进制数每1位，转成对应的4位的一个二进制数即可。
（2）案例：请将0x23B转成二进制。

2 原码、反码、补码

计算机底层存储数据时使用的是二进制数字，但是计算机在存储一个数字时并不是直接存储该数字对应的二进制数字，而是存储该数字对应二进制数字的补码。

2.1 机器数

一个数在计算机的存储形式是二进制数，我们称这些二进制数为机器数。机器数可以是有符号的，用机器数的最高位存放符号位，0表示正数，1表示负数。

2.2 真值

因为机器数带有符号位，所以机器数的形式值不等于其真实表示的值（真值），以机器数10000001为例，其真正表示的值（首位为符号位）为-1，而形式值（首位就是代表1）为129；因此将带符号的机器数的真正表示的值称为机器数的真值。

2.3 原码

原码的表示与机器数真值表示的一样，即用第一位表示符号，其余位表示数值。

• 正数的原码：就是它对应的二进制数。
• 负数的原码：它的绝对值对应的二进制数，且最左边位变为1。
• 0的原码：仍然是0。
  十进制的正负1，用8位二进制的原码表示如下：

+1 原码：[ 0000 0001 ]
-1 原码：[ 1000 0001 ]

2.4 反码

• 正数的反码：和原码相同。
• 负数的反码：在其原码的基础上，符号位不变，其余各位取反。
• 0的反码：仍然是0。
  十进制的正负1，用8位二进制的反码表示如下：

+1 原码：[ 0000 0001 ]  反码：[ 0000 0001 ]
-1 原码：[ 1000 0001 ]  反码：[ 1111 1110 ]

需要注意的是，反码通常是用来由原码求补码或者由补码求原码的过渡码。

2.5 补码

• 正数的补码：和原码、反码相同。
• 负数的补码：反码的基础上加1。
• 0的补码：仍然是0。
  十进制的正负1，用8位二进制的补码表示如下：

+1 原码：[ 0000 0001 ]  反码：[ 0000 0001 ]  补码：[ 0000 0001 ]
-1 原码：[ 1000 0001 ]  反码：[ 1111 1110 ]  补码：[ 1111 1111 ]

2.6 总结

（1）正数的原码、反码、补码都一样，三码合一。
（2）负数的反码：它的原码符号位不变，其它位取反（0 -> 1，1 -> 0）；负数的补码：它的反码+1。
（3）0的反码，补码都是0。

2.7 计算机为什么用补码

计算机内部在处理减法计算的时候会将其转换为加法计算的形式，以简化硬件设计和提高计算效率。如2-2可以写成2+（-2）
最高位表示符号位由于符号位的存在，如果使用原码表示，会导致计算结果不正确。补码的设计可以巧妙地让符号位参与运算，并且可以得到正确的计算结果。

2.8 计算案例

需求：计算10 – 12，使用补码描述计算机内部的计算过程。