- K-means
①无监督学习方法
②分类问题,输入分类数目,初始化中心位置
③硬分类方法,以距离度量
④迭代分类为聚类 - 过程:
初始化中心位置
对各个数据点,计算与它们到每个中心点的距离,把它归为与之最近中心点
重新计算中心点,中心点位置发生变化
执行多个迭代之后,RSS收敛满足,得到最终分类
Kmeans(
InputArray data,
InputOutputArray bestLabels,
TermCriteria criteria,
int attempts,
int flags,
OutputArray centers=noArray());
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace std;
using namespace cv;
//https://www.tinymind.net.cn/articles/1f381f6d949505
//随机产生sampleCount(范围[1,1000])个二维样本,随机产生clusterCount(范围[2,5])个类别,
//每个类别的样本数据都服从高斯分布,该高斯分布的均值是随机的,方差是固定的;
//然后对这sampleCount个样本数据使用kmeans算法聚类3次,取其中最好的一次作为最后的结果,
//最后将不同的类用不同的颜色显示出来;
int main(int argc, char** argv)
{
Mat src(500, 500, CV_8UC3);//建立一个500X500,3通道的彩色图
RNG rng;//随机数产生器
const int MAX_CLUSTERS = 5; //最大聚类数目
//为最大的5种聚类分配5种不同的颜色,用以区分不同类的数据
Scalar color[] =
{
Scalar(0,0,255),
Scalar(0,255,0),
Scalar(255,0,0),
Scalar(0,255,255),
Scalar(255,0,255),
};
//分类
int clusterCount = rng.uniform(2, MAX_CLUSTERS);//在[2,5]之间产生均匀随机数作为该次实验聚类个数,保证至少有两个及以上待聚类,才能体现kmeans方法
cout << "number of clusters聚类数目 :" << clusterCount << endl;
int sampleCount = rng.uniform(5, 1001);//在[5,1001]之间均匀随机产生所有样本点//数据样本数大于聚类数
cout << "number of sampleCount采样点数目 :" << sampleCount << endl;
Mat points(sampleCount,1, CV_32FC2);//存放样本点,是sampleCount行2通道的行向量
Mat centers(clusterCount, 1, points.type());//用来存储聚类后的中心点
Mat labels;
// 生成随机数
for (int i = 0; i < clusterCount; i++)
{
Point center;//均匀随机产生初始化聚类中心
center.x = rng.uniform(0, src.cols);
center.y = rng.uniform(0, src.rows);
//随机数据块//rowRange(int x, int y):(其中y应小于等于行数,例如一个矩阵最大为5行,那么y最大为4)的创建矩阵范围为从x行为首行开始,往后数y-x行。
Mat pointChunk = points.rowRange(i * sampleCount / clusterCount,//每个聚类中样本数目都是sampleCount / clusterCount
i == clusterCount - 1 ? //K至少能取到0,1,保证有两个及以上待聚类
sampleCount :(i + 1)*sampleCount / clusterCount);
//每个聚类的随机初始化中心作为均值,方差都相等
rng.fill(pointChunk, RNG::NORMAL, Scalar(center.x, center.y), Scalar(src.cols*0.05, src.rows*0.05));
}
randShuffle(points, 1, &rng);//随机打乱points里面的样本点,注意points和pointChunk是共用数据的
// 使用KMeans
kmeans(points,
clusterCount,//K聚类数
labels,//包含每个数据点的最终聚类索引
TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 10, 0.1), //可以指定要运行算法的最大迭代次数,或指定一个最小距离,
//当两次迭代之间聚类中心移动的距离小于给定的最小距离时,停止迭代
3, //运行attemptsc次,每次从一组新的种子点开始,并记录最佳效果//聚类3次,取结果最好的那次
KMEANS_PP_CENTERS,//KMEANS_PP_CENTERS表示初始化中心使用Arthur and Vassilvitskii的kmeans++初始化方法
centers);//聚类中心放到centers中心
src == Scalar::all(255);//初始src
// 用不同颜色显示分类,根据不同聚类中心使用不同的颜色绘制出来
for (int j = 0; j < sampleCount; j++)
{
int index = labels.at<int>(j);//聚类个数索引值
Point center_p = points.at<Point2f>(j);
circle(src, center_p,2, color[index], -1, 8);
}
// 每个聚类的中心来绘制圆
for (int k = 0; k < centers.rows; k++)
{
int x = centers.at<float>(k, 0);
int y = centers.at<float>(k, 1);
cout << "聚类中心点为 c.x: " << x << "," << "c.y: " << y << endl;
circle(src, Point(x, y), 40, color[k], 1, LINE_AA);
}
imshow("K-means", src);
waitKey(0);
return 0;
}
输出结果:
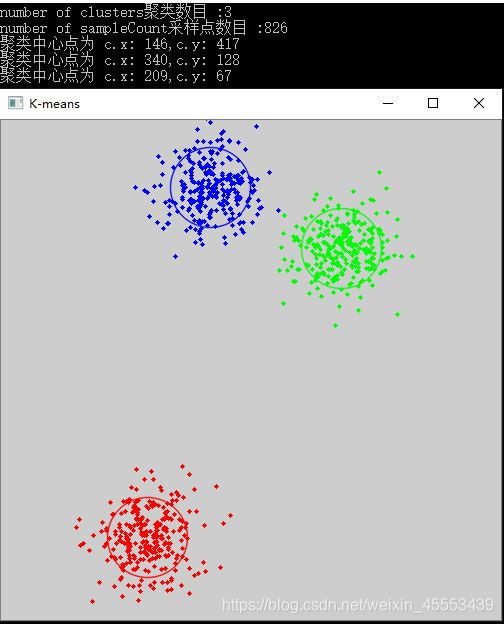










 本文介绍了OpenCV中使用K-means进行图像分割的方法,它是一种无监督学习算法,适用于分类问题。通过设定分类数目和初始中心位置,K-means采用硬分类策略以距离作为判断标准。经过多次迭代,直到类间平方和(RSS)收敛,最终实现数据的聚类划分。文章详细阐述了K-means的执行过程,包括中心点的初始化、数据点的分类和中心点的重新计算,最后输出分类结果。
本文介绍了OpenCV中使用K-means进行图像分割的方法,它是一种无监督学习算法,适用于分类问题。通过设定分类数目和初始中心位置,K-means采用硬分类策略以距离作为判断标准。经过多次迭代,直到类间平方和(RSS)收敛,最终实现数据的聚类划分。文章详细阐述了K-means的执行过程,包括中心点的初始化、数据点的分类和中心点的重新计算,最后输出分类结果。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








