73.矩阵置零

题目：

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

示例 1：

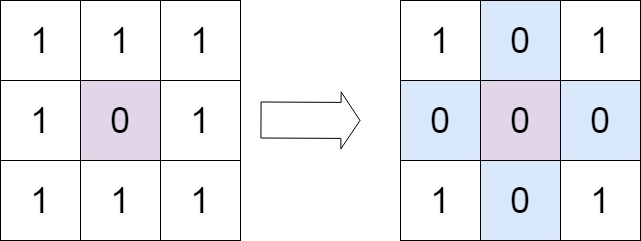
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

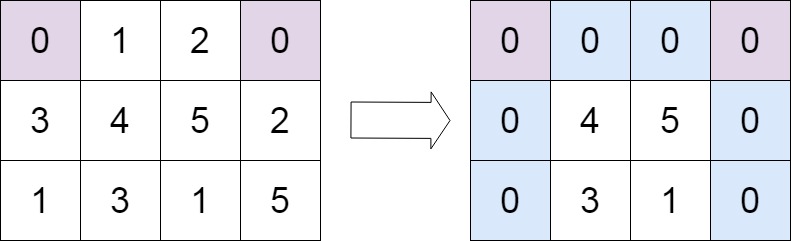
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

• m == matrix.length
• n == matrix[0].length
• 1 <= m, n <= 200
• -231 <= matrix[i][j] <= 231 - 1

进阶：

• 一个直观的解决方案是使用  O(mn) 的额外空间，但这并不是一个好的解决方案。
• 一个简单的改进方案是使用 O(m + n) 的额外空间，但这仍然不是最好的解决方案。
• 你能想出一个仅使用常量空间的解决方案吗？

解题思路：

定义行和列的数组，如果矩阵中出现了0，则将行和列的数组置1，遍历矩阵，如果行或者列的flag值为1则认为该行或者列出现了0元素，这种时间复杂度为，空间复杂度为O(M+N)

代码：

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        M = len(matrix)
        N = len(matrix[0])
        row = [0]*M
        col = [0]*N
        for i in range(M):
            for j in range(N):
                if matrix[i][j]==0:
                    row[i], col[j]=1, 1
        for i in range(M):
            for j in range(N):
                if col[j]or row[i]==1:
                    matrix[i][j]=0