Java-算法-动态规划-背包问题

ForwardSummer

已于 2022-10-03 12:01:31 修改

阅读量7.5k

点赞数 17

CC 4.0 BY-SA版权

分类专栏： leetcode Java 文章标签：动态规划算法

于 2022-05-29 22:39:59 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_45532984/article/details/124925721

本文详细介绍了背包问题的三种类型：最原始的背包问题、0/1背包和完全背包。通过理论推导、状态转移方程、代码实现和LeetCode实战题目解析，阐述了动态规划在解决背包问题中的应用，包括状态压缩和滚动数组等技巧。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

看完本篇文章可以再多练习相似题目

算法-动态规划-背包问题-附一

一. 背包问题介绍

1. 最原始的背包问题

给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。

2. 暴力解法

在最原始的背包问题中，我们假设每种物品只可以选一次，那么背包问题就可以转换为更为具体的0/1背包问题，即每种物品要与不要的问题。这种问题用暴力解法可以用回溯来做，即每种物品开始直接选择，然后递归，然后撤回对该物品的选择。

3. 引入动态规划

假设我们的物品的重量为w[i],物品的价值为v[i]，动态规划产生的dp表为dp[i][j]，其中i代表第i件物品，j代表此时背包的容量，那么我们需要求得的结果即为dp[i][j]代表此时来到第i件物品和背包容量为j的时候我们所能获得的最大价值。

二. 0/1背包

假设此时背包容量为10，物品为四个，我们的重量数组为w[i] = {2,3,4,7},对应的价值v[i] = {1,3,5,9}

1. dp表

dp表的行代表物品，列代表背包容量。在从j=0到j=10的过程中，我们逐渐从小到大一致满足我们的背包能放下的物品的最大值。

dp表的第一列很好确定，因为背包容量是0，所以都是0，dp表的第一行也好确定，就是当容量为j的时候能不能放下第一个物品。

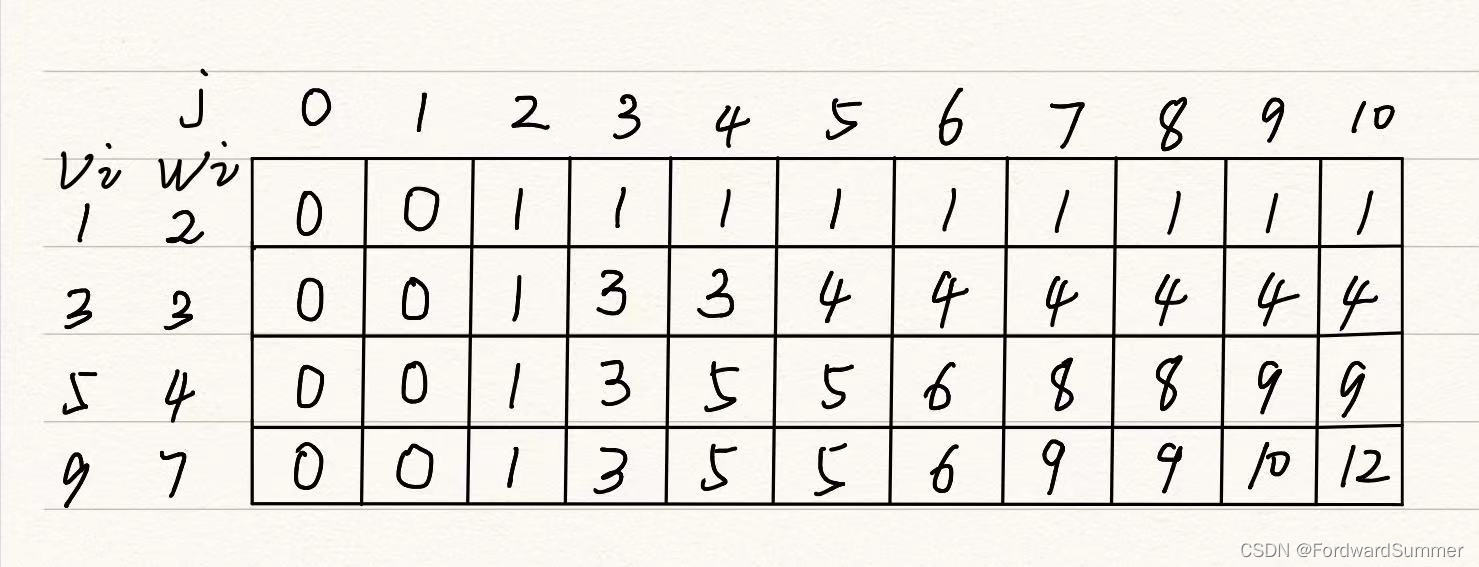
而剩下的部分就要一个一个推得。需要考虑能不能放下当前物品，能放下的话还需要和不要当前物品的情况比较。

2. 状态转移方程

观察上方的dp表，我们发现当前状态的值由上一层的状态确定。当前背包可能获得的最大价值由两部分决定，一是放当前物品，另外一个是不要当前物品，两者取最大值。

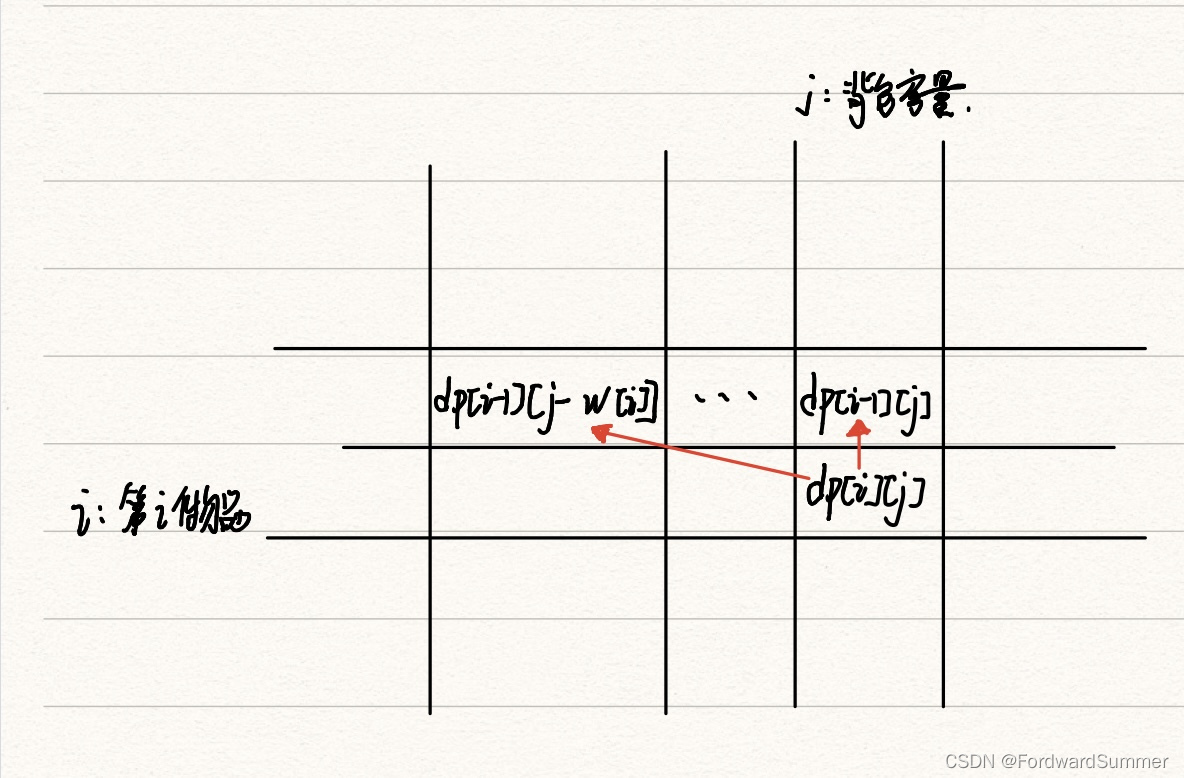
当前背包容量大于当前物品，那么最大值为

$dp[i][j] = Max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])$

因为我们需要放此时的物品，所以对应的需要减去当前的重量，剩下的重量是上层背包的容积，而上层我们已经求出。

当前背包容量小于当前物品，那么最大值为上一层背包所能放下的最大价值

$dp[i][j] = dp[i-1][j]$

3. 代码实现

class Solution {
    public int maxValue(int N, int C, int[] v, int[] w) {
        int[][] dp = new int[N][C+1];
        // 第一件物品
        for (int i = w[0]; i <= C; i++) {
            dp[0][i] = v[0];
        }
        // 其余物品
        for (int i = 1; i < N; i++) {
            for (int j = 0; j <= C; j++) {
                if(j < w[i]){
                    dp[i][j] = dp[i-1][j];
                }
                else{
                    dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
                }
            }
        }
        return dp[N-1][C];
    }
}

4. 滚动数组

在获得状态转移方程时我们发现，当前层的值只与上一层有关，此时我们可以进行状态压缩，把n行的dp数组压缩成一行。即一维数组在不断变化，变化的过程就是二维数组中的每一行。不过要注意的是，因为在滚动的时候，我们需要用到dp[c-nums[i]]的信息，c是此时背包容量，nums[i]是当前物品的重量，这意味着从前往后压缩的时候，会覆盖掉此前的信息，但是回看滚动数组的使用方法，我们用的是上一层即上一次的结果，这意味着我们把这一层原来的信息进行了更新，会导致错误，所以一般我们进行状态压缩使用滚动数组的时候一般是从后往前压缩，这点尤其需要注意。

class Solution {
    public int maxValue(int N, int C, int[] v, int[] w) {
        int[]dp = new int[C+1];
        for (int i = 0; i < N; i++) {
            for (int j = C; j >= w[i]; j--) {
                 dp[j] = Math.max(dp[j],dp[j-w[i]]+v[i]);
            }
        }
        return dp[C];
    }
}

压缩后的状态太庄毅方程：

$dp[j] = Max(dp[j],dp[j-w[i]]+v[i])$

5. leetcode实战

（1）leetcode416分割等和子集

给你一个只包含正整数的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

输入：nums = [1,5,11,5] 输出：true 解释：数组可以分割成 [1, 5, 5] 和 [11]

输入：nums = [1,2,3,5] 输出：false 解释：数组不能分割成两个元素和相等的子集

解法一：二维数组

class Solution {
    public boolean canPartition(int[] nums) {
        int sum = 0;
        int len = nums.length;
        for(int i : nums) sum += i;
        if(sum%2 != 0) return false;
        int target = sum/2;
        int[][] dp = new