NC68 跳台阶

题目解析
这是一道经典的递推题目，你可以想如果青蛙当前在第n级台阶上，那它上一步是在哪里呢？

显然，由于它可以跳1级台阶或者2级台阶，所以它上一步必定在第n-1,或者第n-2级台阶，也就是说它跳上n级台阶的跳法数是跳上n-1和跳上n-2级台阶的跳法数之和。

设跳上 i 级台阶有 f(n)种跳法，则它跳上n级的台阶有

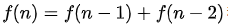
种跳法。

然后，我们又思考初始（(n-2)<=0）的情况，跳上1级台阶只有1种跳法，跳上2级台阶有2种跳法，最终我们得到如下的递推式：

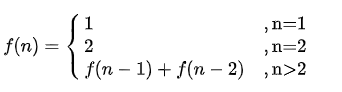
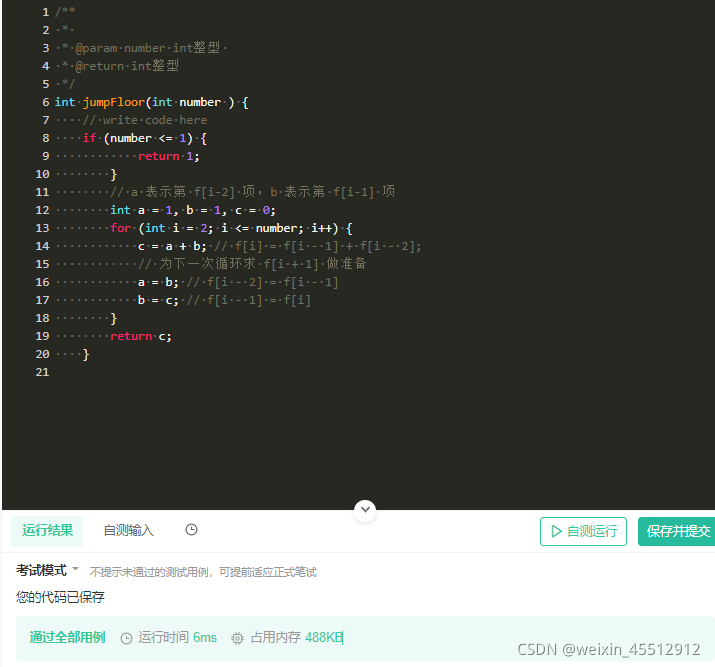
int jumpFloor(int number ) {
// write code here
if (number <= 1) {
return 1;
}
// a 表示第 f[i-2] 项，b 表示第 f[i-1] 项
int a = 1, b = 1, c = 0;
for (int i = 2; i <= number; i++) {
c = a + b; // f[i] = f[i - 1] + f[i - 2];
// 为下一次循环求 f[i + 1] 做准备
a = b; // f[i - 2] = f[i - 1]
b = c; // f[i - 1] = f[i]
}
return c;
}

参考链接：
跳台阶（递推）