机器学习 | 梯度下降原理及Python实现

相关文章：

机器学习 | 目录

机器学习 | 网络搜索及可视化

监督学习 | 线性回归原理及Sklearn实现

An overview of gradient descent optimization algorithms

梯度下降优化算法综述

Keras 中的优化程序

1. 梯度下降

梯度下降（Gradient Descent）是一种非常通用的优化算法，能够为大范围的问题找到最优解。梯度下降的中心思想就是迭代地调整参数从而使成本函数最小化。

假设你迷失在山上的迷雾中，你能够感觉到的只有你脚下路面的坡度。快速到达山脚的策略就是沿着最陡的方向下坡。这就是梯度下降的做法：通过测量参数向量 $\theta$ 相关的误差函数的局部梯度，并不断沿着梯度的方向调整，演到梯度降为 0，到达最小值！

具体来说，首先使用一个随机的 $\theta$ 值（这被称为随机初始化），然后逐步改进，每次踏出一步，每一步都尝试降低一点成本函数（如在线性回归中采用 MSE），直到算法收敛出一个最小值，如下所示：

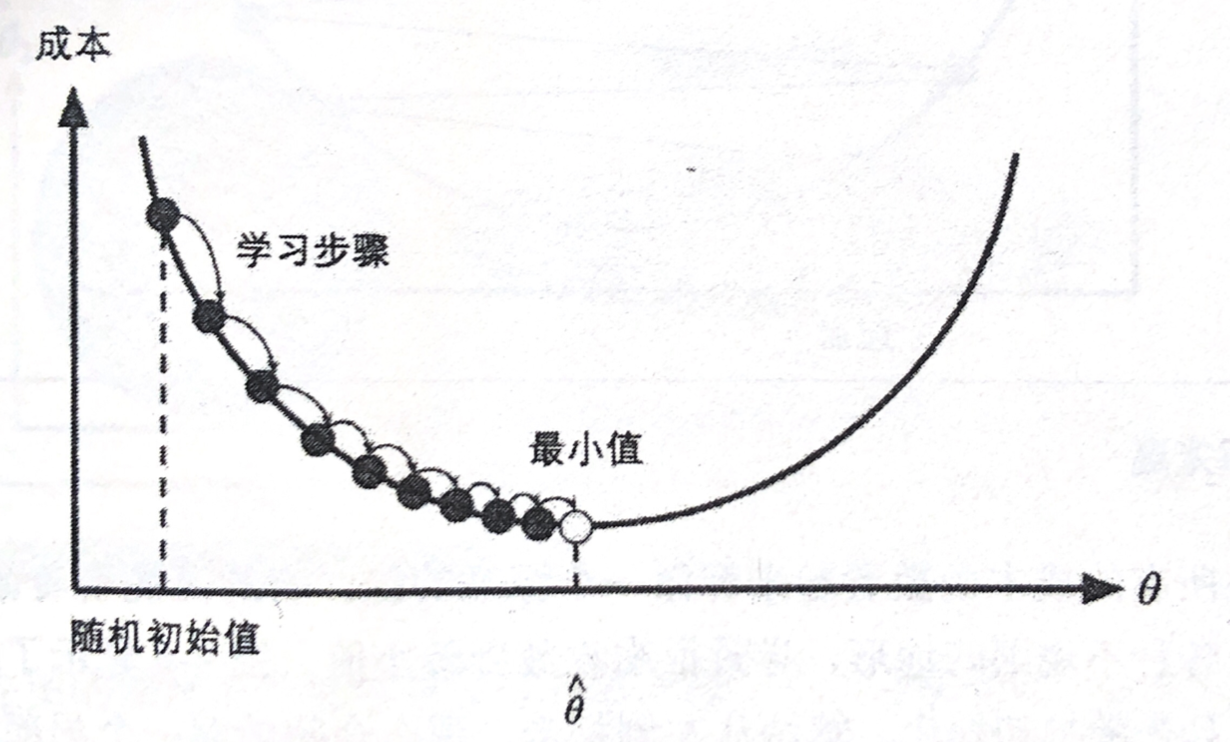
梯度下降中一个重要参数就是每一步的步长，这却取决于超参数学习率（Learning Rate）。如果学习率态度，算法需要经过大量迭代才能收敛，这将耗费很长时间，如图所示，学习率太低：

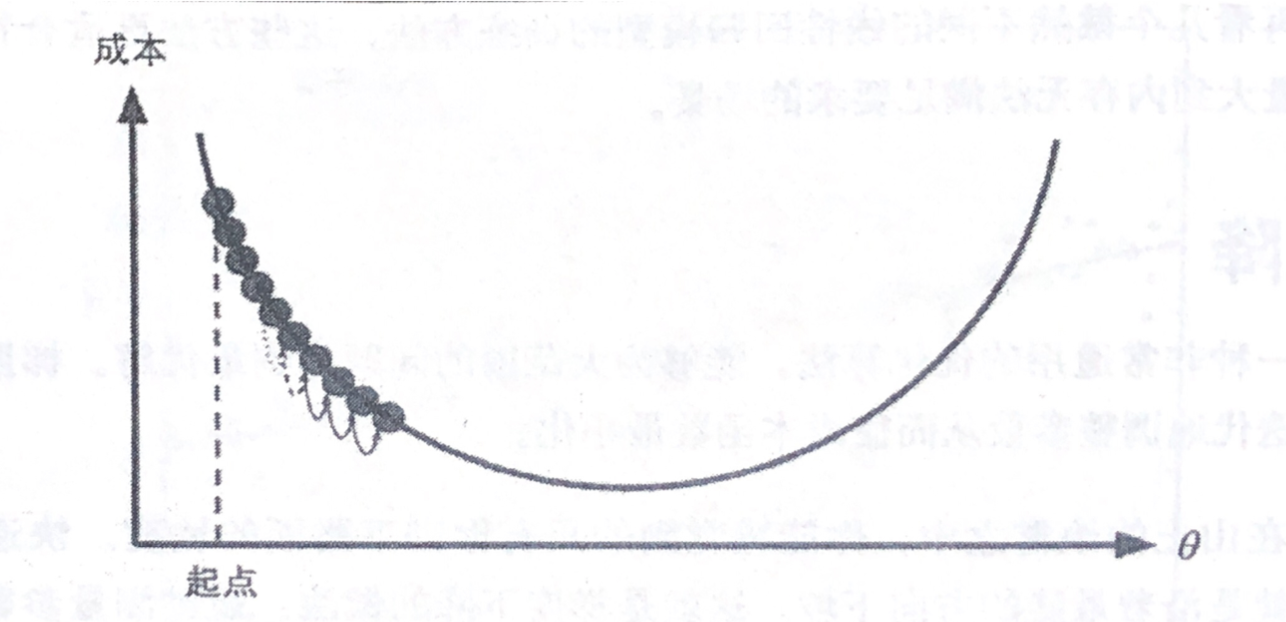
反过来说，如果学习率太高，那可能会越过山谷直接到达山的另一边（并没有蓝精灵），设置有可能比之前的起点还要高。这会导致算法发散，值越来越大，最后无法找到好的解决方案，如下所示，学习率太高：

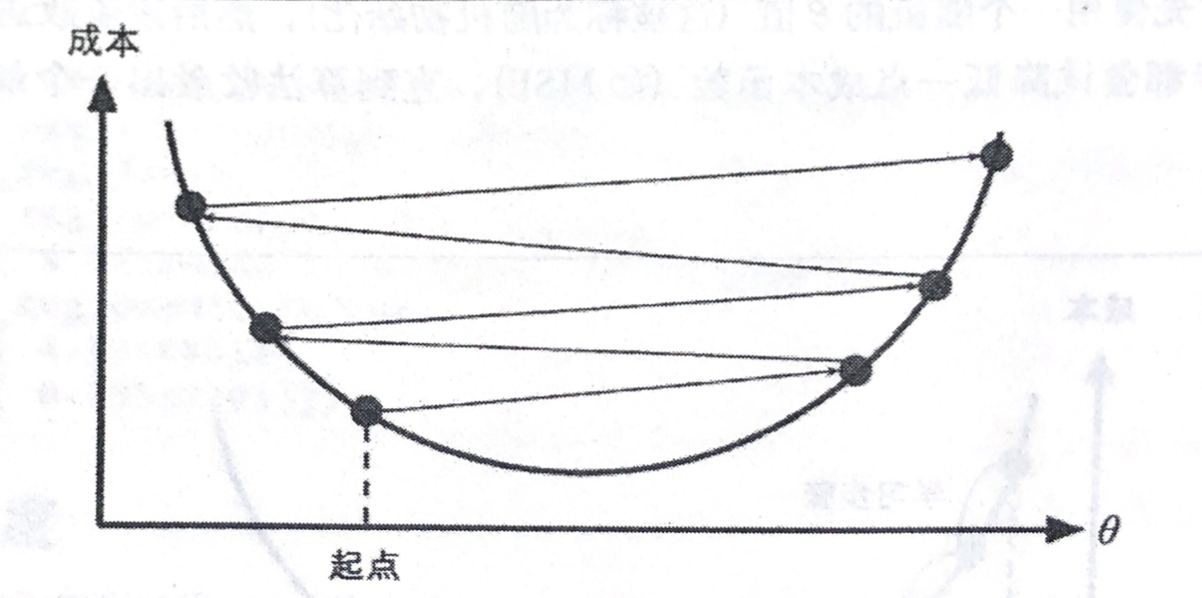
最后，并不是所有的成本函数看起来都像一个漂亮的碗。有的可能看着像洞、像山脉、像高原或者是各种不规则的地形，导致很难收敛到最小值。

下图显示了梯度下降的两个主要挑战：如果随机初始化，算法从左侧起步，那么会收敛到一个局部最小值，而不是全局最小值。如果从右侧起步，那么需要经过很长时间才能越过整片高原，如果停下来太早，将永远达不到全局最小值。

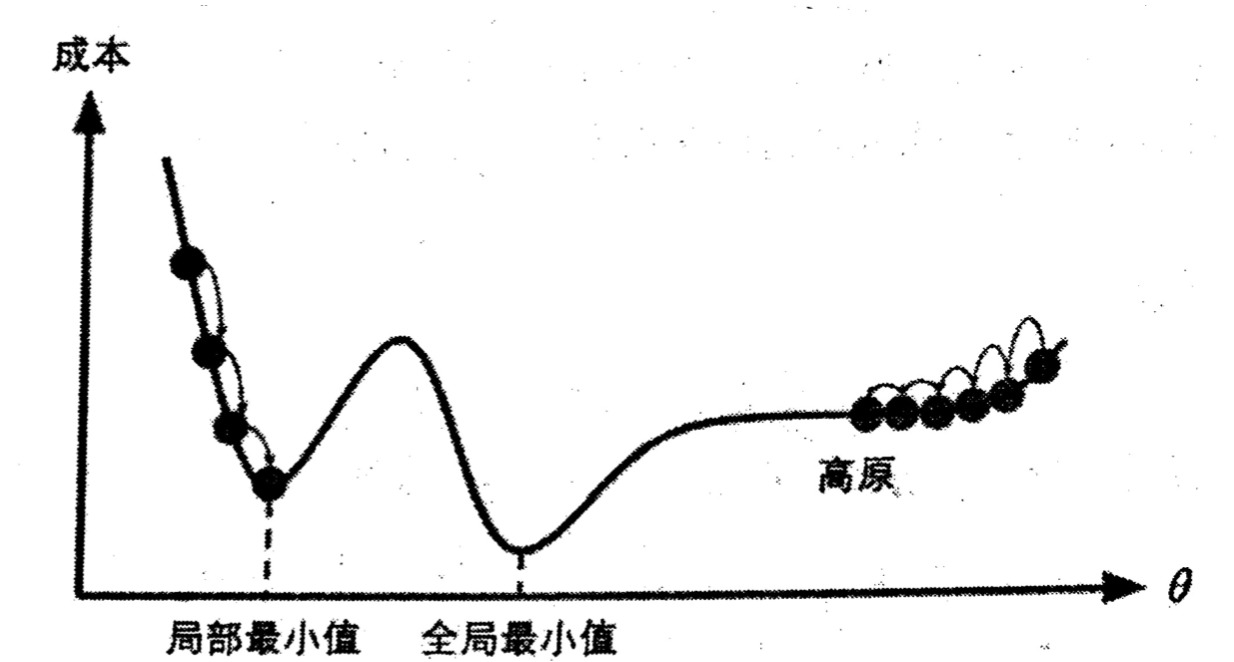
以线性回归模型为例，其成本函数 MSE 恰好是个凸函数，这意味着连接曲线上任意两个点的线段永远不会跟曲线相交。也就是说不存在局部最小，只有一个全局最小值，它同时也是一个连续函数，所以斜率不会产生陡峭的变化（即汉族利普西茨条件）。这两点保证了即便是乱走，梯度下降都可以趋近到全局最小值（只要等待时间足够长，学习率也不是太高）。

成本函数虽然是碗状的，但如果不同特征的尺寸差别巨大，那它可能是一个非常细长的碗。如下图所示的梯度下降，左边的训练集上特征 1 和特征 2 具有相同的数值规模，而右边的训练集上，特征 1 的数值则比特征 2 要小得多（因为特征 1 的值较小，所以 ${\theta }_1$ 需要更大的变化来来影响成本函数，这就是为什么碗形会沿着 ${\theta }_1$ 轴拉长）。

特征值无缩放和特征值缩放的梯度下降：

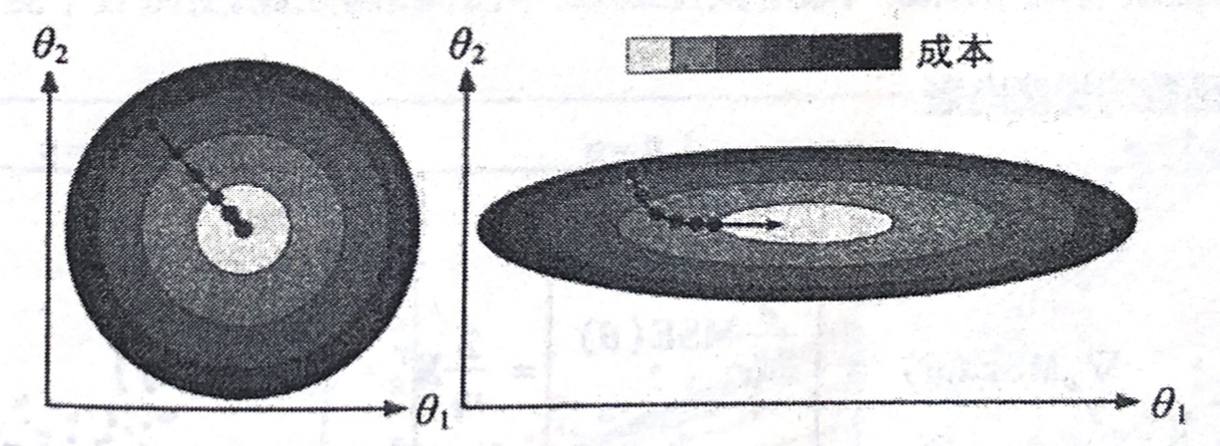
正如你所见，左图的梯度下降算法直接走向最小值，可以快速到达。而在右图中，显示沿着与全局最小值方向近乎垂直的方向前进，接下来是一段几乎平坦的长长的山谷。最后还是会抵达最小值，但是这需要花费大量的时间。

应用梯度下降时，需要保证全有特征值的大小比例都差不多（比如使用 Sklearn 的 StandardScaler 类），否则收敛的时间会长很多。

这张图也说明，训练模型也就是搜寻使成本函数（在训练集上）最小化的参数组合。这是模型参数空间层面上的搜索：模型的参数越多，这个空间的维度就越多，搜索就越难。同样是在干草堆里找寻一根针，在一个三百维的空间里就比一个在三维空间里要棘手得多，幸运的是，对于成本函数为凸函数的，针就躺在碗底。^[1]

1.1 批量梯度下降（BGD）

要实现梯度下降，需要计算每个模型关于参数 ${\theta }_j$ 的成本函数的梯度。换言之，需要计算的是如果改变 ${\theta }_j$，成本函数会改变多少，即偏导数。

以线性回归的成本函数 $MSE$ 为例，其偏导数为：

$$\begin{array}{rl}\frac{\partial }{\partial {\theta }_j}MSE(\theta )& =\frac{\partial }{\partial {\theta }_j}(\frac{1}{m}\sum _{i=1}^m({\theta }^T\cdot X^{(i)}-y^{(i)}{)}^2)\\ & =\genfrac{}{}{0ex}{}{}{m}\end{array}$$