HDU2199(实数二分)

最新推荐文章于 2022-02-10 05:42:03 发布

原创最新推荐文章于 2022-02-10 05:42:03 发布 · 303 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#沙雕 #acm

ACM 专栏收录该内容

52 篇文章

订阅专栏

本文介绍了一种使用二分查找算法求解复杂方程根的方法。通过设定搜索区间和精度，实现对8x^4+7x^3+2x^2+3x+6=Y的实数根的精确查找。

又到了二分的季节！
其实二分很简单，主要是二分的思想
原题：
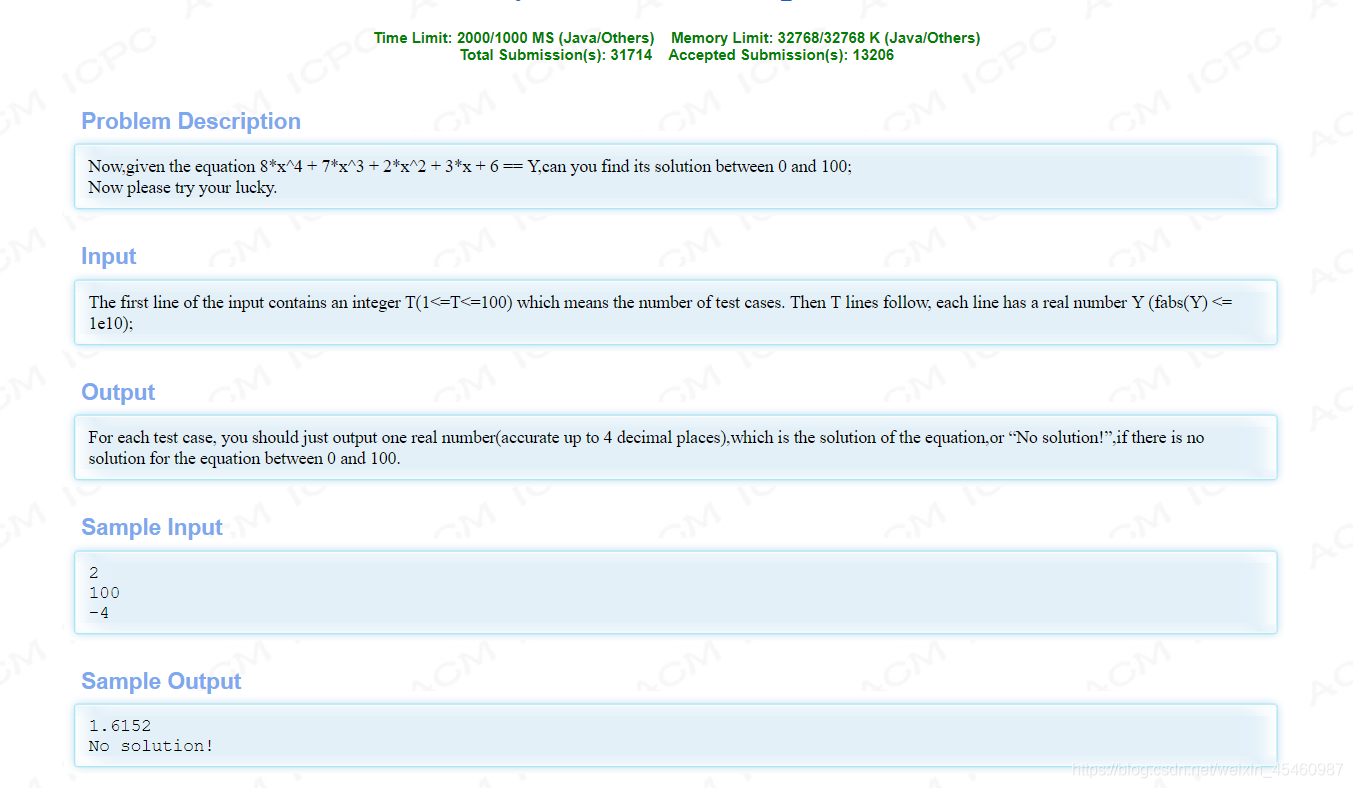
在这里插入图片描述
题目大意：求出方程 8x^4 + 7x^3 + 2x^2 + 3x + 6 == Y的根（我也不知道这个缩进很迷）
我拿到题目懵了一下，第一思路是四次方程怎么解，后来我傻了，有计算机我干嘛自己算？？！！
二分查找答案！

又到了喜闻乐见的贴代码环节

#include<stdio.h>
#include<algorithm>
using namespace std;
double function(double x)
{
	return 8 * pow(x, 4) + 7 * pow(x, 3) + 2 * pow(x, 2) + 3 * x + 6;
}
int main()
{
	double y, y1, y2, y3, left, right, mid;
	int t;
	scanf_s("%d", &t);
	while (t--)
	{
		left = 0;
		right = 100;
		scanf_s("%lf", &y);
		y1 = function(left) - y;
		y2 = function(right) - y;
		if (y1 > 0 || y2 < 0)
			printf("No solution!\n");
		else
		{
			for (int i = 0; i < 100; i++)
			{
				mid = (left + right)/2;
				y3 = function(mid) - y;
				if (y3 >= 0)
					right = mid;
				else
					left = mid;
			}
			printf("%0.4lf\n", mid);
		}
	}
	return 0;
}

首先呢，我估计答案在0-100之间，（右边界可以再大一些）
注意用double型
然后判断是不是对于我输入的y值有解，如果说left值-y还比0大是不是就是无解呢（因为left=0呀），如果right值-y比0还小是不是就是无解呢（因为right大于0呀）
有解的话，因为是实数二分，我习惯循环100次，这样应该就可以达到题目的精度要求了或者你用while控制也是可以的（left-right>0.00000001）类似这样
是不是还挺清楚的亚子；
不说了
新的风暴已经出现
下次见