Transformer理解_pe的维度-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_45422462/article/details/115442609

Transformer理解

注：这里不涉及具体的矩阵维度。

背景

Transformer 是 Google Brain团队在 17 年 6 月提出的 NLP 经典之作，由 Ashish Vaswani 等人在 2017 年发表的论文 Attention Is All You Need 中提出。Transformer 在机器翻译任务上的表现超过了 RNN，CNN，只用 encoder-decoder 和 attention 机制就能达到很好的效果，最大的优点是可以高效地并行化。
在这里插入图片描述

Transformer 的 encoder 由 6 个编码器叠加组成，decoder 也由 6 个解码器组成，在结构上都是相同的，但它们不共享权重。整体结构如下：
在这里插入图片描述

细节技术

首先，对里面采用的技术进行理解。

Positional Encoding（PE）

Positional Encoding 是一种考虑输入序列中添加单词位置信息的方法。Encoder 为每个输入embedding 添加了一个向量positional encoding，这些向量符合一种特定模式，可以确定每个单词的位置，或者序列中不同单词之间的距离。例如，input embedding 的维度为4，那么实际的positional encodings如下所示：
在这里插入图片描述
首先，需要明确的是，建模位置信息(无论是绝对位置还是相对位置)并不是必须用到三角函数，否则Fairseq和BERT中使用的positional embedding也不会奏效了。（作者在这里使用正余弦函数，只是根据归纳偏置和一些经验作出的选择。）
不妨从零构想一个位置编码的方法。

首先，给定一个长为T的文本，最简单的位置编码就是计数，即使用PE=pos=0,1,2,⋯,T-1作为文本中每个字的位置编码，但这个序列没有上界。设想一段很长的文本，最后一个字的位置编码非常大，这样会导致：1. 它比第一个字的编码大太多，和字嵌入合并以后难免会导致特征在数值上的倾斜；2. 它比一般的字嵌入的数值要大，难免会抢了字嵌入的“风头”，对模型可能有一定的干扰。从而位置编码最好具有一定的值域范围。
这样就有了第二个版本：使用文本长度对每个位置作归一化，即PE=pos/(T-1)。这样使得所有位置编码都落入[0,1]区间，但是问题也十分显著：不同长度文本的位置编码步长不同。例如在较短的文本中紧紧相邻的两个字的位置编码差异，会和长文本中相邻数个字的两个字的位置编码差异一致。如果使用这种方法，那么在长文本中相对次序关系会被“稀释”。

从而需要positional encoding满足：需要体现同一个单词在不同位置的区别；值域落在一定范围内；需要体现一定的先后次序关系，并且在一定范围内的编码差异不应该依赖于文本长度，具有一定不变性。
文章中使用如下三角函数编码相对位置信息：
在这里插入图片描述
其中PE代表位置编码向量，pos代表单词在文本中的位置，2i代表PE的维度，d_model代表PE向量长度（假设d_model=500，则i=0,…,250，偶数位置采用正弦，奇数位置采用余弦）。

这里不同维度上sin\cos的波长从2π到10000×2π都有；区分了奇、偶数维度的函数形式。这在不同维度上应该用不同的函数操纵位置编码，使得各个位置字符的位置编码各不相同，且每一维度上都包含了一定的位置信息。

下面解释为什么周期函数能够引入位置信息？

从pos出发（各个字符的位置编码）
三角函数拆分公式如下：

那么对于pos+k位置的位置向量某一维2i或2i+1而言，可以表示为pos位置与k位置的位置向量的2i与2i+1维的线性组合，这样的线性组合意味着位置向量中蕴含了相对位置信息，公式如下：
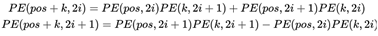
从2i与2i+1出发（同一字符不同维度）
随着维度增加，函数波长（周期）由2π变为10000×2π，也就是其考虑的相对长度变得越来越长，从而提取了不同相对范围内的相对位置信息。例如，可以观察一下下面这个表：

可以发现，越低位的变化越快，红色位置0和1每个数字会变化一次，而黄色位每8个数字才会变化一次。不同频率的sin和cos组合也是同样的道理，通过调整三角函数的频率，我们可以实现这种低位到高位的变化，这样的话位置信息就被包含在PE向量中。
如在下图是20个单词的 positional encoding，每行代表一个单词的位置编码，即第一行是加在输入序列中第一个词嵌入的，每行包含 512 个值，每个值介于 -1 和 1 之间，用颜色表示出来：

可以看到在中心位置分成了两半，因为左半部分的值由一个正弦函数生成，右半部分由余弦函数生成，然后将它们连接起来形成了每个位置的编码向量（也可不用拼接的方式，这里仅仅是举一个例子）。

Multi-head attention

Self-attention

初始化

输入数据（均为Input Embeding，我们假设其输入只有四个单词）
初始矩阵
矩阵W^{q(query-去match)；W}k (key-被q match)；W^v (value-抽取出来的information)。

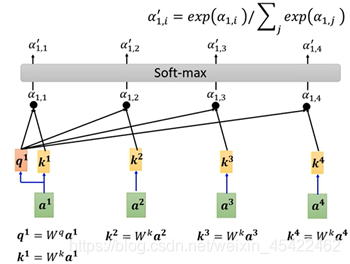
计算单个a^1 对应的注意力b^1

计算步骤如下：

a^1 与矩阵W^q 相乘得到q^1；
a^1 与W^k 相乘得到k^1 、a^2 与W^k 相乘得到k^2 、a^3 与W^k 相乘得到k^3 、a^4 与W^k 相乘得到k^4；
q^1 分别与k^1 、k^2 、k^3 、k^4 相乘得到α_1,1 、α_1,2、α_1,3、α_1,4 ，也就是a^1 这个单词对其他位置单词的注意力是多少；
对α_1,1、α_1,2、α_1,3、α_1,4进行normalizetion，这里采用softmax，从而得到α_1,1^’、α_1,2’、α_1,3^’、α_1,4’；（论文中是现将α_1,1、α_1,2、α_1,3、α_1,4除以k^i向量维度（64）的平方根（8）【解释说这样操作会有更加稳定的梯度】，然后再进行softmax，我们这里忽略），这个位置上的单词将具有最高的softmax分数，但有时候注意与当前单词相关的另一个单词是有用的。
a^1 、a^2 、a^3 、a^4 分别与矩阵W^v 相乘，得到v^1 、v^2 、v^3 、v^4，目的让我们想要关注单词的值保持不变，并通过乘以 0.001 这样小的数字，来淹没不相关的单词；
最后，通过公式

在这里插入图片描述
得到a^1 对应的注意力b^1。

（步骤1到4汇总图）
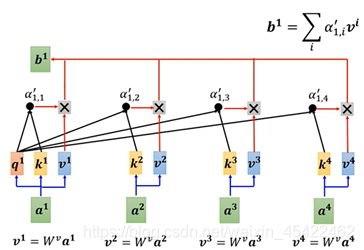
在这里插入图片描述
其余输入embeding对应的注意力b^2 、b^3 、b^4求解过程与上面相同。

强烈推荐李宏毅老师讲解视频，网址：https://www.bilibili.com/video/BV1Xp4y1b7ih?p=1

通过矩阵并行计算整体注意力矩阵O

通过上一小节，其中输入向量a^i 分别与矩阵W^q 、W^k 、W^v 得到对应的q^i 、k^i 、v^i，如下：

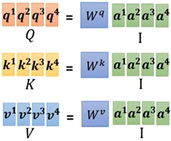
整体汇总如下：
在这里插入图片描述

Scaled dot-Product attention

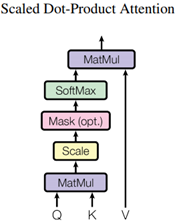
在这里插入图片描述

Multi-head attention

在这里插入图片描述

网络图：

Layer-Normalization(LN)

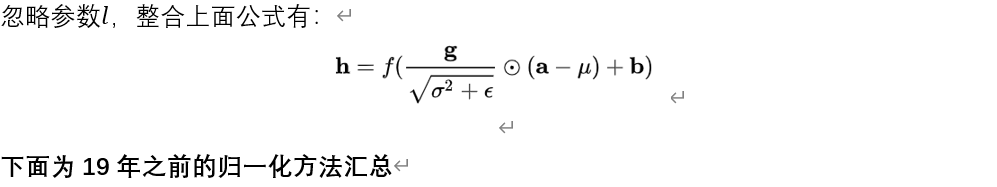
在这里插入图片描述

MASK技术

Transformer中共包含两个mask操作，分别是：
 Padding Mask：让padding(不够长补0)的部分不参与attention操作，在所有的scaled dot-product attention模块中均会用到。
 Sequence Mask：生成当前词语的概率分布时，让程序不会注意到这个词背后的部分，仅在解码阶段的Masked multi-head attention模块中会用到。