基于python3计算机视觉编程(四)图像拼接

最新推荐文章于 2024-08-29 21:54:42 发布

UExplorer

最新推荐文章于 2024-08-29 21:54:42 发布

阅读量933

点赞数 2

分类专栏： Python 文章标签： python 计算机视觉

本文链接：https://blog.youkuaiyun.com/weixin_45389639/article/details/105068342

版权

Python 专栏收录该内容

11 篇文章

订阅专栏

在实验三的博客里面稍微简单的介绍了下基于RANSAC方法的图像拼接，接下来的实验将会着重RANSAC方法的不足以及其解决方案进行实验以及探讨，并随之引出APAP算法。

一. RANSAC简介

RANSAC的全称是“RANdom SAmple Consensus（随机抽样一致）”。它可以从一组包含“局外点”的观测数据集中，通过迭代方式估计数学模型的参数。它是一种不确定的算法，也就是说它有一定的概率得出一个合理的结果，所以为了提高概率必须提高迭代次数。RANSAC是为了解决SIFT特征错误匹配时用的算法。

二. 算法步骤

随机选择四对匹配特征
根据DLT计算单应矩阵 H (唯一解)
对所有匹配点，计算映射误差 $ε = ∣ ∣ p i ’, H p i ∣ ∣$
根据误差阈值，确定inliers
针对最大inliers集合，重新计算单应矩阵 H

在给定若干二维空间中的点，求直线 y=ax+b ，使得该直线对空间点的拟合误差最小。
随机选择两个点，根据这两个点构造直线，再计算剩余点到该直线的距离
给定阈值（距离小于设置的阈值的点为inliers），计算inliers数量
再随机选取两个点，同样计算inliers数量

4.循环迭代，其中inliers最大的点集即为最大一致集，最后将该最大一致集里面的点利用最小二乘拟合出一条直线。

三. 全景拼接

在图像拼接融合的过程中，受客观因素的影响，拼接融合后的图像可能会存在“鬼影现象”以及图像间过度不连续等问题。下图就是图像拼接的一种“鬼影现象”。解决鬼影现象可以采用APAP算法。
在这里插入图片描述
算法流程：

提取两张图片的sift特征点
对两张图片的特征点进行匹配
匹配后，使用RANSAC算法进行特征点对的筛选，排除错误点。筛选后的特征点基本能够一一对应。
使用DLT算法，将剩下的特征点对进行透视变换矩阵的估计。
因为得到的透视变换矩阵是基于全局特征点对进行的，即一个刚性的单应性矩阵完成配准。为提高配准的精度，Apap将图像切割成无数多个小方块，对每个小方块进行单应性矩阵变换。

3.1 最小割问题（最大流问题）

如何消除或弱化拼接缝隙就可以用最小割来解决。
在这里插入图片描述
最小割问题
一个割就是一组边的集合，将给集合边从图中边集合中移除，那么图被分割为两个部分，这两个部分之间没有任何边连接。如果说得有点绕口，那么最简单来说，一块肉被从中间隔开，分成两个部分，中间断开的连接的集合就是割。最小割就是将图切割为两个部分时，代价最小的割的集合，代价就是边上容量的和（S部分到T部分边的容量）。
在这里插入图片描述
最大流问题
假设现在有一个地下水管道网络，有m根管道，n个管道交叉点，现在自来水厂位于其中一个点，向网络中输水，隔壁老王在另外一个点接水，已知由于管道修建的年代不同，有的管道能承受的水流量较大，有的较小，现在求在自来水厂输入的水不限的情况下，能接到的水的最大值？
以上就是最大流问题。
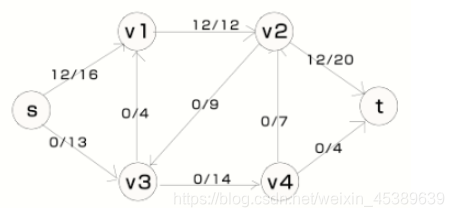
在这里插入图片描述
以下是最大流问题的一些概念
残存网络与增广路径
根据图和各条边上的流可以画出一幅图的残存网络如下所示。上图为流网络，下图为残存网络，其中流网络中边上的数字分别是流量和容量，如10/12，那么10为边上的流量，12为边的容量。残存网络中可能会存在一对相反方向的边，与流网络中相同的边代表的是流网络中该边的剩余容量，在流网络中不存在的边代表的则是其在流网络中反向边的已有流量，这部分流量可以通过“回流”减少。例如，下图残存网络中，边<s,v1>的剩余容量为4，其反向边<v1.s>的值为12，即上图流网络中的边<s,v1>的流量。在残存网络中，值为0的边不会画出，如边<v1,v2>。
在这里插入图片描述
残存网络描述了图中各边的剩余容量以及可以通过“回流”删除的流量大小。在Ford-Fulkerson方法中，正是通过在残存网络中寻找一条从s到t的增广路径，并对应这条路径上的各边对流网络中的各边的流进行修改。如果路径上的一条边存在于流网络中，那么对该边的流增加，否则对其反向边的流减少。增加或减少的值是确定的，就是该增广路径上值最小的边。
Ford-Fulkerson方法
Ford-Fulkerson方法的正确性依赖于这个定理：当残存网络中不存在一条从s到t的增广路径，那么该图已经达到最大流。
Ford-Fulkerson方法的伪代码如下。其中<u,v>代表顶点u到顶点v的一条边，<u,v>.f表示该边的流量，c是边容量矩阵，c(i,j)表示边<i,j>的容量，当边<i,j>不存在时，c(i,j)=0。e为残存网络矩阵，e(i,j)表示边<i,j>的值，当边<i,j>不存在时，e(i,j)=0。E表示边的集合。f表示流网络。

Ford-Fulkerson
    for <u,v> ∈ E
        <u,v>.f = 0
    while find a route from s to t in e
        m = min(<u,v>.f, <u,v>  ∈ route)
        for <u,v> ∈ route
            if <u,v>  ∈ f
                <u,v>.f = <u,v>.f + m
            else
                <v,u>.f = <v,u>.f - m

Ford-Fulkerson方法首先对图中的所有边的流量初始化为零值，然后开始进入循环：如果在残存网络中可以找到一条从s到t的增广路径，那么要找到这条这条路径上值最小的边，然后根据该值来更新流网络。

四. 代码及实验

实验分为两个测试方向：

针对固定点位拍摄多张图片
针对同一场景，更换拍摄位置，分析拼接结果
场景一数据集：

实验结果：
SIFT特征匹配结果：

拼接结果：

这是第一次拼接的结果，可以看出图像拼接存在明显的褶皱，这是因为APAP就算解决了鬼影现象，但是各个图像之间的曝光补偿都存在不同，这也是APAP所面临的挑战。同时在地板上出现了很多小的光斑，猜测原因可能跟博主手机的像素有关，圆形框里面造成的图像扭曲问题在反复调试后发现图片的顺序要从右边往左边排，因为算法的匹配是从最右边的图像计算出来的，代码中有一步骤是将对应的顺序进行颠倒，使其从左边图像开始进行扭曲。

这是第二次的拼接结果，解决了上次拼接造成的扭曲问题，但拼接结果依旧不理想，甚至在本次拼接结果的左半部分没有上次拼接的好，可能造成的原因是匹配的特征点匹配不当造成的图像丢失现象，其二可能是博主拍摄角度的原因。两次实验运行的时间都十分长，应该是和图片的本身的像素值过大有关，所以之后的实验对图片进行了压缩，显著提高了运行效率。但图片也不能被压缩的过小，这样容易丢失某些重要的特征点。即不能太大也不能太小。

场景二数据集：
在这里插入图片描述
实验结果：
SIFT特征匹配结果

拼接结果：

可以看出这次匹配的拼接成功率到达了90%，除了在左上角因为曝光原因造成的褶皱现象，褶皱现象也可以通过multi-band bleing算法使得拼接后的图像拼接痕迹更平滑，不那么明显。总的来说这组实验结果比较理想，SIFT处理不了的景深问题APAP解决了。

代码：

from pylab import *
from numpy import *
from PIL import Image

# If you have PCV installed, these imports should work
from PCV.geometry import homography, warp
# from PCV.localdescriptors import sift
from PCV.localdescriptors import sift

import os
"""
This is the panorama example from section 3.3.
"""

# set paths to data folder
featname = ['E:/test/' + str(i + 1) + '.sift' for i in range(4)]
imname = ['E:/test/' + str(i + 1) + '.jpg' for i in range(4)]

# extract features and match
l = {}
d = {}
for i in range(4):
    sift.process_image(imname[i], featname[i])
    l[i], d[i] = sift.read_features_from_file(featname[i])

matches = {}
for i in range(3):
    matches[i] = sift.match(d[i + 1], d[i])

# visualize the matches (Figure 3-11 in the book)
for i in range(3):
    im1 = array(Image.open(imname[i]))
    im2 = array(Image.open(imname[i + 1]))
    figure()
    sift.plot_matches(im2, im1, l[i + 1], l[i], matches[i], show_below=True)


# function to convert the matches to hom. points
def convert_points(j):
    ndx = matches[j].nonzero()[0]
    fp = homography.make_homog(l[j + 1][ndx, :2].T)
    ndx2 = [int(matches[j][i]) for i in ndx]
    tp = homography.make_homog(l[j][ndx2, :2].T)

    # switch x and y - TODO this should move elsewhere
    fp = vstack([fp[1], fp[0], fp[2]])
    tp = vstack([tp[1], tp[0], tp[2]])
    return fp, tp


# estimate the homographies
model = homography.RansacModel()

fp, tp = convert_points(1)
H_12 = homography.H_from_ransac(fp, tp, model)[0]  # im 1 to 2

fp, tp = convert_points(0)
H_01 = homography.H_from_ransac(fp, tp, model)[0]  # im 0 to 1

tp, fp = convert_points(2)  # NB: reverse order
H_32 = homography.H_from_ransac(fp, tp, model)[0]  # im 3 to 2

# tp,fp = convert_points(3) #NB: reverse order
# H_43 = homography.H_from_ransac(fp,tp,model)[0] #im 4 to 3


# warp the images
delta = 700  # for padding and translation

im1 = array(Image.open(imname[1]), "uint8")
im2 = array(Image.open(imname[2]), "uint8")
im_12 = warp.panorama(H_12, im1, im2, delta, delta)

im1 = array(Image.open(imname[0]), "f")
im_02 = warp.panorama(dot(H_12, H_01), im1, im_12, delta, delta)

im1 = array(Image.open(imname[3]), "f")
im_32 = warp.panorama(H_32, im1, im_02, delta, delta)

figure()

imshow(array(im_32, "uint8"))
axis('off')

show()