[数据结构]树

[数据结构]树

树

树的定义：树是n（n≥0）个结点的有限集，它或为空树（n=0）；或为非空树，对于非空树T：
①有且仅有一个称之为根的结点；
②除根结点之外的其余结点可分为m（m>0）个互不相交的有限集T1，T2，……，Tm，其中每一个集合本身有是一棵树，并且成为根的子树。

树的其他表示方式：广义表、凹入表示、嵌套表示、

树的基本术语：
根——即根结点（没有前驱）
叶子——即终端结点（没有后继）
森林——指m棵不相交的树的集合
有序树——结点各子树从左至右有序，不能互换（左为第一）
无序树——结点各子树可以互换位置
双亲——即上层的那个结点（直接前驱）
孩子——即下层结点的子树的根（直接后继）
兄弟——同一双亲的同层结点（孩子之间互称兄弟）
堂兄弟——即双亲位于同一层的结点（但并非同一双亲）
祖先——即从根到该结点所经分支的所有结点
子孙——即该结点下层子树中的任一结点
结点——即树的数据元素
结点的度——结点挂接的子树数
结点的层次——从根到该结点的层数（根结点算第一层）
终端结点——即度为0的结点，即叶子
分支结点——即度不为0的结点（也成为内部结点）
树的度——所有结点度中的最大值
树的深度（或高度）——指所有结点中最大的层数

二叉树

二叉树的定义：二叉树是n（n≥0）个结点所构成的集合，它或为空树（n=0）；或为非空树，对于非空树T：
①有且仅有一个称之为根的结点；
②除根结点之外的其余结点可分为两个互不相交的子集T1和T2，分别称为T的左子树和右子树，且T1和T2本身又都是二叉树。
二叉树的基本特点
● 结点的度≤2
● 有序树（子树有序，不能颠倒）
二叉树的五种表示形态

二叉树的性质

● 性质1：在二叉树的第i层上至多有2^i-1个结点。
● 性质2：深度为k的二叉树至多有2^k-1个结点。
● 性质3：对于任何一棵二叉树，若2度的结点数有n₂个，则叶子数n₀必定为n₂+1（即n₀=n₂+1）。
● 性质4：具有n个结点的完全二叉树的深度必为[log₂n]+1。
● 性质5：对完全二叉树，若从下至上、从左至右编号，则编号为i的结点，其左孩子编号必为2i，其右孩子编号必为2i+1；其双亲的编号必为i/2。

特殊形态的二叉树

满二叉树
定义：一棵深度为k且有2^k-1个结点的二叉树。
特点：每层都“充满”了结点。
完全二叉树
定义：深度为k的，有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应。
满二叉树与完全二叉树的区别：满二叉树是叶子一个也不少的树，而完全二叉树虽然前n-1层是满的，但最底层却允许在右边缺少连续若干个结点。满二叉树是完全二叉树的一个特例。

二叉树的抽象数据类型定义

二叉树的顺序存储

实现：按满二叉树的结点层次编号，一次存放二叉树中的数据元素。
特点：结点间关系蕴含在其存储位置中，浪费空间，适于存满二叉树和完全二叉树。

二叉树的链式存储

二叉树的应用

● 利用二叉树求解表达式的值
● 用二叉树表示算数表达式
● 计算二叉树结点总数
● 计算二叉树叶子结点的总数
● 计算二叉树的深度

遍历二叉树

遍历定义：按某条搜索路线遍访每个结点且不重复（又称周游）。
遍历用途：它是树结构插入、删除、修改、查找和排序运算的前提，是二叉树一切运算的基础和核心。
遍历规则

口诀：
DLR——先序遍历，即先根再左再右
LDR——中序遍历，即先左再根再右
LRD——后序遍历，即先左再右再根
先序遍历算法

//算法5.1.1 先序遍历的递归算法
void PreorderTraverse(BiTree T){
	if(T==NULL)
	return OK;//空二叉树
	else
	{
		cout<<T->data;//访问根结点
		PreorderTraverse(T->lchild);//递归遍历左子树
		PreorderTraverse(T->rchild);//递归遍历右子树
	}
}

中序遍历算法

//算法5.1.2 中序遍历的递归算法
void InOrderTraverse(BiTree T){
	if(T==NULL)
	return OK;//空二叉树 
	else
	{
		InOrderTraverse(T->lchild);//递归遍历左子树 
		cout<<T->data;//访问根结点 
		InOrderTraverse(T->rchild);//递归遍历右子数 
	}
} 

后序遍历算法

//算法5.1.3 后序遍历的递归算法
void PostorderTraverse(BiTree T){
	if(T==NULL)
	return OK;//空二叉树
	else{
		PostorderTraverse(T->lchild);//递归遍历左子树 
		PostorderTraverse(T->rchild);//递归遍历右子数
		cout<<T->data;//访问根结点
	}
}

遍历算法的分析
如果去掉输出语句，从递归的角度看，三种算法是完全相同的，或者说三种算法的访问路径是相同的，只是访问结点的时机不同。

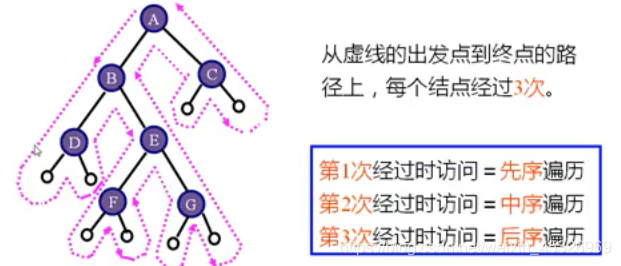
时间效率O(n)：每个结点只访问一次
空间效率O(n)：栈占用的最大辅助空间

中序遍历二叉树T的非递归算法

void InOrderTraverse1(BiTree T)
{ 
  //算法5.2 中序遍历二叉树T的非递归算法
LinkStack S; BiTree p;
BiTree q=new BiTNode;
InitStack(S); p=T;
while(p||!StackEmpty(S))
{
if(p) 
{            
Push(S,p); //p非空根指针进栈，遍历左子树
p=p->lchild;
}       
else
{            
Pop(S,q);               //p为空根指针退栈，访问根结点，遍历右子树
cout<<q->data;
p=q->rchild; 
}
} // while
} // InOrderTraverse

二叉树的建立算法

//算法5.3 先序遍历的顺序建立二叉链表
void CreateBiTree(BiTree &T){
//按先序次序输入二叉树中结点的值（一个字符），创建二叉链表表示的二叉树T
char ch;
cin >> ch;
if(ch=='#')  T=NULL; //递归结束，建空树
else{
T=new BiTNode;
T->data=ch; //生成根结点
CreateBiTree(T->lchild); //递归创建左子树
CreateBiTree(T->rchild); //递归创建右子树
} //else
} //CreateBiTree

复制二叉树算法

//算法5.4 复制二叉树
void Copy(BiTree T, BiTree &NewT){
	if(T!=NULL)
	{
		NewT=new BiTNode;
		NewT->data=T->data; //生成根结点
		Copy(T->lchild,NewT->lchild); //递归创建左子树
		Copy(T->rchild,NewT->rchild); //递归创建右子树
	}
	else
	{
		NewT=NULL;
	}
}

计算二叉树的深度算法

//算法5.5 计算二叉树的深度
int Depth(BiTree T){
	int l,r,d;
	if(T!=NULL)
	{
		l=Depth(T->lchild);
		r=Depth(T->rchild);
		d=1+(l>r?l:r);
	}
	else
	{
		d=0;
	}
	return d;
}

统计二叉树中结点的个数算法

//算法5.6 统计二叉树中结点的个数
int NodeCount(BiTree T){
	if(T==NULL)
	return 0;
	else 
	return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
} 

统计二叉树中叶子结点的个数算法

//算法5.7 统计二叉树中叶子结点的个数
void Leafnum(BiTree T,int &n){
	if(T!=NULL){
		if((T->lchild==NULL)&&(T->rchild==NULL))
		{
			n++;
		}
		Leafnum(T->lchild,n);
		Leafnum(T->rchild,n);
	}
}

线索化二叉树

线索化二叉树的几个术语

线索：指向结点前驱和后继的指针
线索二叉树：加上线索的二叉树（图形样式）
线索链表：加上线索二叉链表
线索化：对二叉树以某种次序遍历使其变为线索二叉树的过程