学习笔记-电动力学 第五章

第五章 静磁学

核心问题：稳恒电流产生磁场

5-1 洛伦兹力

$$\vec{F}=Q\vec{v}\times \vec{B}$$
Notes:1、洛伦兹力不做功，在电场存在的情况下$\vec{F}=Q(\vec{E}+\vec{v}\times \vec{B})$
2、在洛伦兹力作用下，粒子会做回旋运动。
通电导线在磁场中受力$$\overrightarrow{F_{mag}}=\int \vec{I}\times \vec{B}dl$$ $$\vec{I}=\lambda \vec{v}$$
电流面密度 $$\vec{k}=\sigma \vec{v}$$
体电流密度 $$\vec{J}=\rho \vec{v}$$
电流的连续性方程 $$\frac{\partial \rho }{\partial t}=-\nabla \cdot \vec{J}$$

5-2 Biot-Savart 定理

稳恒电流产生的磁场由毕奥·萨伐尔定理给出：$$\vec{B}(\vec{r})=\frac{{\mu }_0}{4\pi }\int \frac{\vec{I}\times \vec{r}}{r^2}$$
$$\mathbf{B}(\mathbf{r})=\frac{{\mu }_0}{4\pi }\int \frac{\mathbf{I}\times \hat{\mathbf{r}}}{r^2}\mathrm{d}{l}^{\prime }=\frac{{\mu }_0}{4\pi }I\int \frac{\mathrm{d}{\mathbf{l}}^{\prime }\times \hat{\mathbf{r}}}{r^2}$$
Note:这里的$\vec{r}=\vec{r}-{\vec{r}}^{\prime }$
对于体电流和面电流：
$$\mathbf{B}(\mathbf{r})=\frac{{\mu }_0}{4\pi }\int \frac{\mathbf{K}\left({\mathbf{r}}^{\prime }\right)\times \hat{\mathbf{r}}}{r^2}\mathrm{d}{\mathbf{a}}^{\prime },\mathbf{B}(\mathbf{r})=\frac{{\mu }_0}{4\pi }\int \frac{\mathbf{J}\left({\mathbf{r}}^{\prime }\right)\times \hat{\mathbf{r}}}{r^2}\mathrm{d}{\tau }^{\prime }$$

磁场的散度和旋度

$$\nabla \cdot \vec{B}=0$$ 积分形式为：$$\oint \vec{B}\cdot d\vec{S}=0$$
$$\nabla \times \vec{B}={\mu }_o\vec{J}$$积分形式为：$$\oint \vec{B}\cdot d\vec{l}={\mu }_0{I}_{enc}$$(安培定理）
Remarks:可以利用安培定理进行求解的构型有：
1、无限长螺线管
2、无限长直电流
3、无限大平面
4、环形线圈

5-3 磁矢势

由$\nabla \cdot \vec{B}=0$，可以得到$\vec{B}=\nabla \times \vec{A}$
通过适当的变换${\vec{A}}^{\prime }=\vec{A}+\nabla \lambda$ , 我们可以令${\nabla }^2\vec{A}=-{\mu }_0\vec{J}$
假设无穷远处$\vec{J}=0$,则我们可以写出：$$A(r)=\frac{{\mu }_0}{4\pi }\int \frac{J\left(r^{\prime }\right)}{r}d{\tau }^{\prime }$$，对于面电流和线电流而言：

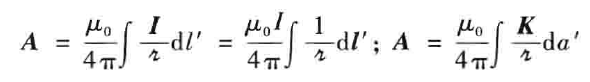
磁矢势的多级展开，$$\mathbf{A}(\mathbf{r})=\frac{{\mu }_{0}I}{4\pi }\left[\frac{1}{r}\oint \mathrm{d}{l}^{\prime }+\frac{1}{r^2}\oint r^2\cos {\theta }^{\prime }\mathrm{d}{l}^{\prime }+\frac{1}{r^3}\oint {\left(r^{\prime }\right)}^2\left(\frac{3}{2}{\cos }^2{\theta }^{\prime }-\frac{1}{2}\right)\mathrm{d}{l}^{\prime }+\cdots \right]$$其中，第一项为单极项，第二项为偶极项，第三项为四极项。
特别的，对于偶极项：$$A_{偶极}(r)=\frac{{\mu }_0}{4\pi }\frac{m\times r}{r^2}$$其中$$\mathbf{m}\equiv I\int \mathrm{d}\mathbf{a}=Ia$$
$${\vec{B}}_{偶极}(r)=\nabla \times \vec{A}=\frac{{\mu }_{0}m}{4\pi r^3}(2\cos \theta \hat{r}+\sin \theta \hat{\theta })$$
$${\vec{B}}_{偶极}(r)=\frac{{\mu }_0}{4\pi }\frac{1}{r^3}[3(m\cdot \hat{r})\hat{r}-m]$$

5-4 磁场的边界条件

$${\mathbf{B}}_{上}-{\mathbf{B}}_{下}={\mathbf{\mu }}_0(\mathbf{K}\times \hat{\mathbf{n}})$$
$${\vec{A}}_{上}={\vec{A}}_{下}$$
$$\frac{\partial {\vec{A}}_{上}}{\partial n}-\frac{\partial {\vec{A}}_{下}}{\partial n}=-{\mathbf{\mu }}_0\vec{K}$$