数据结构与算法知识整理（五）---m叉搜索树与B树

本篇内容以知识整理为主，会结合萨特吉-萨尼的数据结构书籍和网络上的一些知识整理做一下总结，语言使用c++，有问题请及时指正，欢迎交流。

1、m叉搜索树

1、m叉搜索树的定义

定义： m 叉搜索树（m-way search tree）可以是一棵空树，如果非空，它必须满足以下特征：

1. 在相应的扩充搜索树中（用外部节点替换零指针），每个内部节点最多可以有m 个子女及1～m-1个元素（外部节点不含元素和子女）。
2. 每个含p个元素的节点，有p+1个子女。
3. 考察含p 个元素的任意节点。设k1 , …, kp 是这些元素的关键值。这些元素升序排列，即有k1 < k2 < . . . <kp。设c0 , c1 , …, cp 是节点的p+1个孩子。以c0 为根的子树中的元素关键值小于k1，而以cp 为根的子树中的元素关键值大于kp，并且以ci 为根的子树中的元素关键值会大于ki 而小于ki+1，其中1≤i≤p。
   

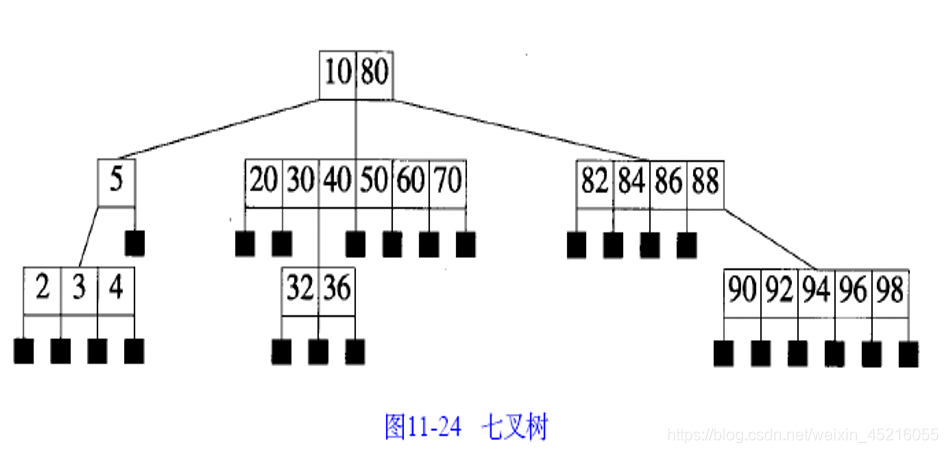
2、m叉搜索树的高度

由于高度为h的m叉搜索树中元素的个数在h到mh-1之间，所以一棵n元素的m叉搜索树的高度在logm(n+1)到n之间。

2、B树

1、m序B-树

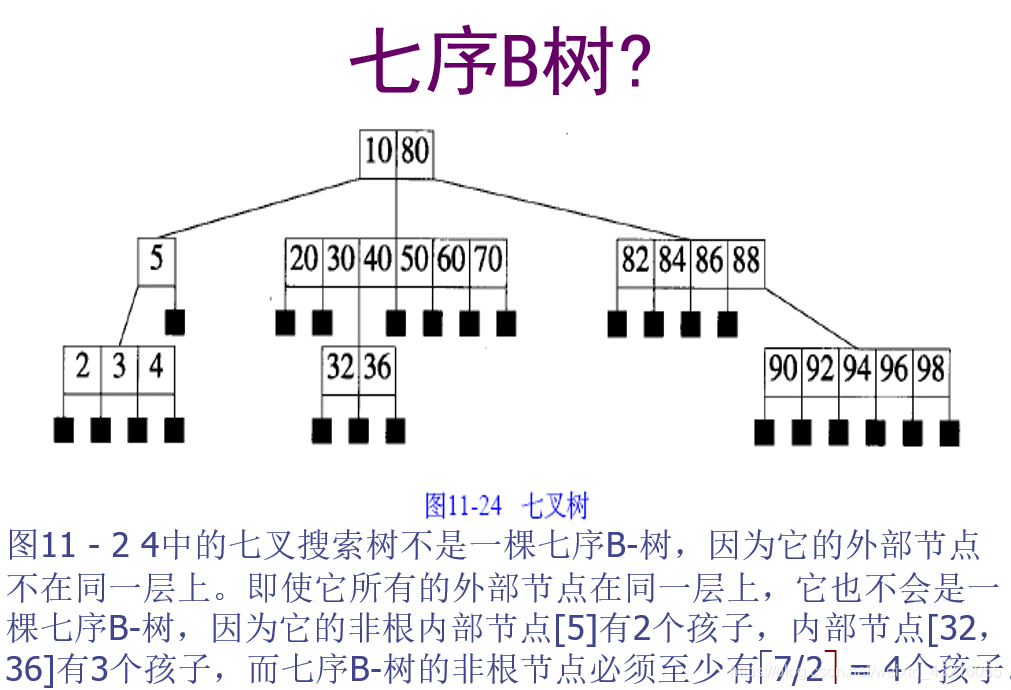
定义：m树B树（B-Tree of order m）是一棵m叉搜索树，如果B树非空，那么相应的扩充树满足以下特征：

1. 根节点至少有两个孩子
2. 除了根节点以外，所有内部节点至少有[m/2]个孩子
3. 所有外部节点位于同一层上，叶节点不包含任何关键字信息
4. 每个节点至多有m个孩子
5. 有k个孩子的非叶节点恰好包含k-1个关键字
   

2、B-树的高度

3、B-树的插入

将一个元素插入B-树中时，首先要检查具有相同关键值的元素是否存在，如果找到了这个元素，那么插入失败，因为不允许重复值存在。
当搜索不成功时，便可以将元素插入到搜索路径中所遇到的最后一个内部节点处。
饱和？当新元素需要插入到饱和节点中时，饱和节点需要被分开。

3、B+树

B+树是一种常用于文件组织的B-树的变形树，一棵m阶的B+树与B树的差异在于：

1. 所有的叶子结点中包含了全部关键字的信息，及指向含这些关键字记录的指针，且叶节点依照关键字的大小从小到大顺序链接。
2. 非叶节点仅具有索引作用，节点中仅含有其子树（根节点）中最大（或最小）关键字。（B树键值只出现一次）
3. 叶节点的子树棵数可以多于m，也可以少于m。
   

4、堆

堆是一棵完全二叉树，如果每个节点的值都大于或等于其子节点（如果有的话）的值，那么这个堆是最大堆；相反的，如果每个节点的值都小于或等于其子节点的值，那么这个堆是最小堆，
堆是完全二叉树，可用一维数组有效的描述。拥有n个元素的堆高度为[log2(n+1)]。

#define MaxData 。。。//建议设一个堆的最大元素值作为哨兵，在对堆进行操作时你会发现很方便。当然只是建议。
typedef struct node *Heap;
struct node{
	ElementType *Elements;//储存堆元素的指针
	int size;//当前堆元素个数
	int Capacity;//	堆容量
};
Heap CreateMaxHeap(int maxsize)
{
	Heap H=new node;
	H->Elements=new ElementType[maxsize+1];
	H->size=0;
	H->Capacity=maxsize;
	H->Elements[0]=MaxData;//设一个堆的最大元素值放在0位置上
	return H;
}

1、最大堆的插入

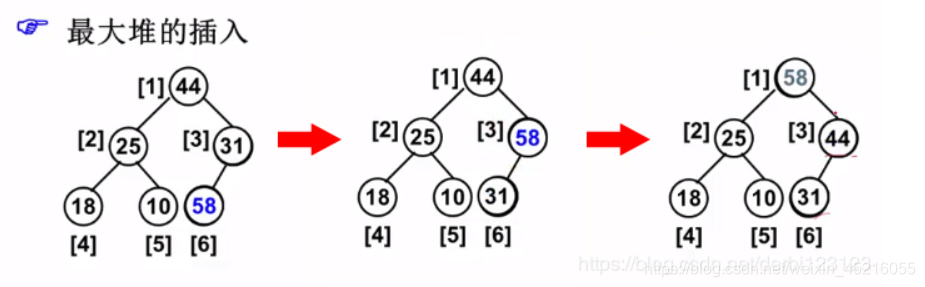
bool Insert( Heap H, ElementType X )
{ /* 将元素X插入最大堆H，其中H->Data[0]已经定义为哨兵 */
    int i;
  
    if ( IsFull(H) ) { 
        printf("最大堆已满");
        return false;
    }
    i = ++H->Size; /* i指向插入后堆中的最后一个元素的位置 */
    for ( ; H->Data[i/2] < X; i/=2 )
        H->Data[i] = H->Data[i/2]; /* 上滤X */
    H->Data[i] = X; /* 将X插入 */
    return true;
}

2、最大堆的删除

删除操作其实是删除根节点。我们的做法是让最后一个叶子结点代替根节点，先满足结构特性，在进行调整满足有序性。

#define ERROR -1 /* 错误标识应根据具体情况定义为堆中不可能出现的元素值 */
ElementType PercDown(Heap H)//返回根节点
//把根节点为H->Elements[p]的子堆调整为最大堆。
{
	if ( IsEmpty(H) ) {
        printf("最大堆已为空");
        return ERROR;
    }
	int child,parent;
	ElementType MAX=H->Elements[1];//根节点
	ElementType tmp=H->Elements[H->size--];//--是因为删除了根节点。
	for(parent=p;parent*2<=H->size;parent=child){
		child=parent*2;//得到左子节点序号
		if( child!=H->size && H->Elements[child] < H->Elements[child+1] )
			//取左右子节点中大的那个(毕竟要让最大的在上面)
			child+=1;
		if(tmp>=H->Elements[child]) break;
		else	//如果子节点大于父节点就要让子节点代替父节点
			H->Elements[parent]=H->Elements[child];
	}
	H->Elements[parent]=tmp;
	return MAX;
}

3、最大堆的创建

从第一个具有孩子的节点开始，这个元素在数组中的位置为i=[n/2]，如果以这个元素为根的子树已是最大堆，则此时不需调整，否则必须调整子树使之成为堆。
随后，继续检查以i-1,i-2等节点为根的子树，直到检查到整个二叉树的根节点（其位置为1）

int N,data[N];//这样定义全局变量不对，只是用于代表序列
Heap CreateMaxHeap(//参数根据需要写)//要对上面的建堆函数做一些小修改，其实本就应灵活变通
{
	Heap H=new node;
	H->Elements=new ElementType[N+1];
	for(int i=1;i<=N;i++){
		H->Elements[i]=data[i-1];//data是从0到n-1。
	}
	H->size=0;
	H->Capacity=N;
	H->Elements[0]=MaxData;//设一个堆的最大元素值放在0位置上
	return H;
}
void PercDown(Heap H,int p)//下滤
//把根节点为H->Elements[p]的子堆调整为最大堆。
{
	int child,parent;
	ElementType tmp=H->Elements[p];//用tmp把子堆的根节点存起来
	for(parent=p;parent*2<=H->size;parent=child){
		child=parent*2;//得到左子节点序号
		if( child!=H->size && H->Elements[child] < H->Elements[child+1] )
			//取左右子节点中大的那个(毕竟要让最大的在上面)
			child+=1;
		if(tmp>=H->Elements[child]) break;
		else	//如果子节点大于父节点就要让子节点代替父节点
			H->Elements[parent]=H->Elements[child];
	}
	H->Elements[parent]=tmp;
}
void BuildMaxHeap(Heap H)
{//从最后一个父节点开始下滤，方便的一批
	for(int i=H->size/2;i>=1;i--)
		PercDown(H,i);
}

4、堆排序

堆排序（Heap　sort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以用到上一次的排序结果，所以不像其他一般的排序方法一样，每次都要进行n-1次的比较，复杂度为O(nlogn)。
算法步骤：

1）利用给定数组创建一个堆H[0…n-1]（我们这里使用最小堆），输出堆顶元素

2）以最后一个元素代替堆顶，调整成堆，输出堆顶元素

3）把堆的尺寸缩小1

4） 重复步骤2，直到堆的尺寸为1
详细代码后面补到排序算法整理中

5、霍夫曼树