
请问怎么理解让w尽量往0靠近,就相当于减少了网络复杂度?这个网络复杂度怎么考虑的呢,是因为w趋于0的话,相当于不用计算了,或计算量变小了
l1正则啊,可以筛选特征,
L1正则相当于减小模型复杂度,可以防止过拟合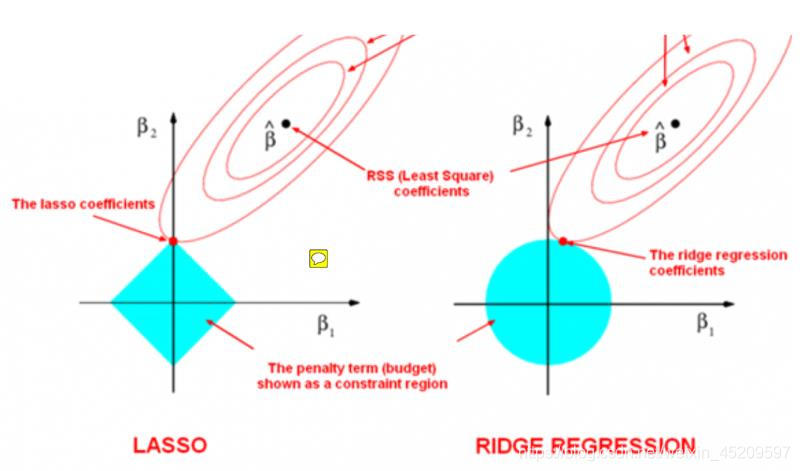
w趋向于零,w的高次变的更加接近零,相当于舍去高非线性,模型趋向线性,可以降低过拟合,
写的是趋于0,结果是产生了不少0,也就是筛选特征了,让参数稀疏,所以可以理解成网络复杂度降低了
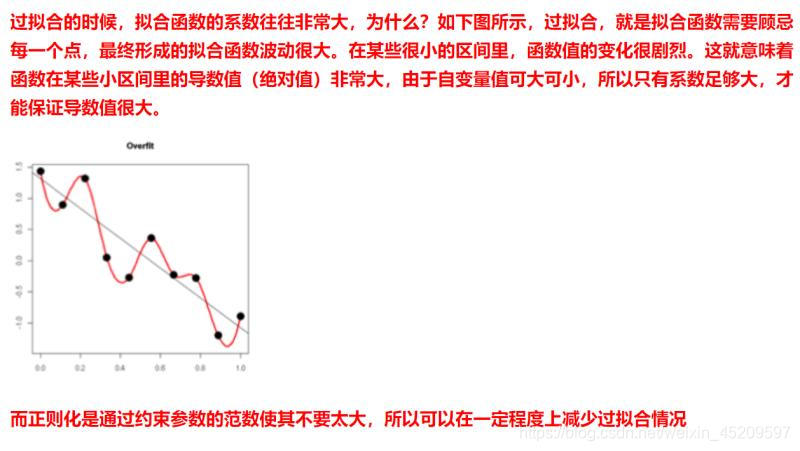
1.为啥要保证倒数足够大
2.正则化和上面的介绍有啥关系
保证导数值大
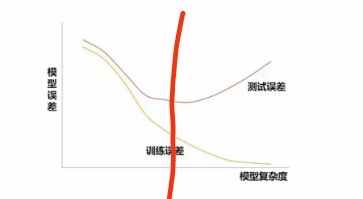
上面的导数值大就是说你的拟合函数波动太大,不稳定,正则化可以使函数系数不那么大,函数波动小一些,更平滑,鲁棒性更强
能否详细讲解下正则化如何通过约束参数的范数使其不要太大,这里是关于L2正则化让w变小,w变小可以防止过拟合的数学解释

正则化是个引入先验分布或者是添加约束条件,让模型简化,不去拟合数据集的噪音,对应到你那个图里,就是导数小一点,不要去拟合所有的样本
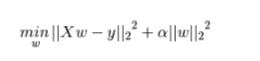
对于它原来的损失函数,也就是经验风险,不是越小越好
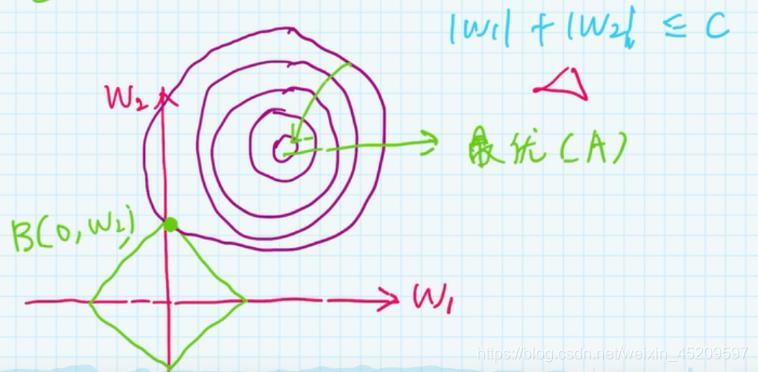
正则化思想就是没有取原来损失函数最小的w值,而是移了个位置,因为约束条件,也就是加上正则化后w取值必须在菱形框里,单从两个w的角度来看,就是他们的相交点,原来最佳位置是那个圆的圆心
根据kkt条件,因是必要条件,所以可以构造拉格朗日乘数法(也就是我们看到的结构风险),取得最优解时的w也就是有取值范围(比如|w1|+|w2|<c)的w的解

L1正则化可以使w中一部分变为0,因为相交时其横坐标也就是Wi为0,当高维时也就有更多的Wi为0,相当于使得多项式的次数变小
L2正则化是使得Wi尽可能变小,接近0,因为约束条件,wi都在某个小范围之内。多项式次数未改变,只是使得曲线没有经过所有的点,因为原来的损失函数训练时并没有让它非常接近0,这样也可以避免学习过多的特征
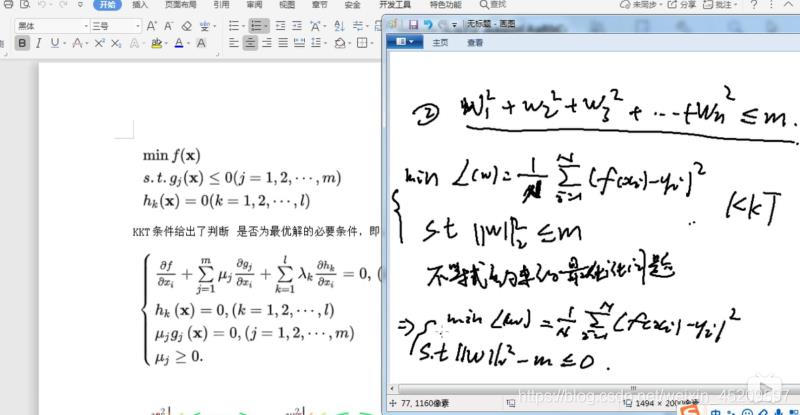
正则
最新推荐文章于 2024-08-03 05:56:08 发布




















 5773
5773

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








