上机笔记3.1

最新推荐文章于 2022-10-03 15:38:23 发布

Agsol

最新推荐文章于 2022-10-03 15:38:23 发布

阅读量296

点赞数

分类专栏：算法笔记文章标签：测试用例算法 c++

本文链接：https://blog.youkuaiyun.com/weixin_45176825/article/details/122512879

版权

算法笔记专栏收录该内容

23 篇文章

订阅专栏

文章目录

*3.1 PAT B1011

输入格式：

输入第 1 行给出正整数 T (≤10)，是测试用例的个数。随后给出 T 组测试用例，每组占一行，顺序给出 A、B 和 C。整数间以空格分隔。

输出格式：

对每组测试用例，在一行中输出 Case #X: true 如果 A+B>C，否则输出 Case #X: false，其中 X 是测试用例的编号（从 1 开始）。

输入样例：

4
1 2 3
2 3 4
2147483647 0 2147483646
0 -2147483648 -2147483647

输出样例：

Case #1: false
Case #2: true
Case #3: true
Case #4: false

#include<stdio.h>
//本比方式
//int main() {
//	int n;
//	long long a, b, c;
//	int bout[10] = { -1 };
//	scanf("%d", &n);
//	for (int i = 0; i < n; i++) {
//		scanf("%lld %lld %lld", &a, &b, &c);
//		if (a + b > c) {
//			bout[i] = 1;
//		}
//		else {
//			bout[i] = 0;
//		}
//	}
//	for (int i = 0; i < n; i++) {
//		if (bout[i] == 1) {
//			printf("Case #%d: true\n",i+1);
//		}
//		else if (bout[i] == 0) {
//			printf("Case #%d: false\n",i+1);
//		}
//	}
//	return 0;
//}
//算法笔记方式
int main() {
	int n;
	long long a, b, c;
	scanf("%d", &n);
	for (int i = 0; i < n; i++) {
		scanf("%lld%lld%lld", &a, &b, &c);
		if (a + b > c) {
			printf("Case #%d: true\n", i + 1);
		}
		else {
			printf("Case #%d: false\n", i + 1);
		}
	}
}

*3.1 PAT B1016

正整数 A 的“D**A（为 1 位整数）部分”定义为由 A 中所有 D**A 组成的新整数 P**A。例如：给定 A=3862767，D**A=6，则 A 的“6 部分”P**A 是 66，因为 A 中有 2 个 6。

现给定 A、D**A、B、D**B，请编写程序计算 P**A+P**B。

输入格式：

输入在一行中依次给出 A、D**A、B、D**B，中间以空格分隔，其中 0<A,B<109。

输出格式：

在一行中输出 P**A+P**B 的值。

输入样例 1：

3862767 6 13530293 3

输出样例 1：

输入样例 2：

3862767 1 13530293 8

输出样例 2：

#include<stdio.h>

int main() {
	long long a, da, b, db;
	scanf("%lld%lld%lld%lld", &a, &da, &b, &db);
	long long pa = 0, pb = 0;
	while (a != 0) {
		if (a % 10 == da) {
			pa = pa * 10 + da;
			
		}
		a /= 10;
	}
	while (b != 0) {
		if (b % 10 == db) {
			pb = pb * 10 + db;
			
		}
		b /= 10;
	}
	printf("%lld\n", pa + pb);
	return 0;

}

*3.1 PAT B1026

要获得一个 C 语言程序的运行时间，常用的方法是调用头文件 time.h，其中提供了 clock() 函数，可以捕捉从程序开始运行到 clock() 被调用时所耗费的时间。这个时间单位是 clock tick，即“时钟打点”。同时还有一个常数 CLK_TCK，给出了机器时钟每秒所走的时钟打点数。于是为了获得一个函数 f 的运行时间，我们只要在调用 f 之前先调用 clock()，获得一个时钟打点数 C1；在 f 执行完成后再调用 clock()，获得另一个时钟打点数 C2；两次获得的时钟打点数之差 (C2-C1) 就是 f 运行所消耗的时钟打点数，再除以常数 CLK_TCK，就得到了以秒为单位的运行时间。

这里不妨简单假设常数 CLK_TCK 为 100。现给定被测函数前后两次获得的时钟打点数，请你给出被测函数运行的时间。

输入格式：

输入在一行中顺序给出 2 个整数 C1 和 C2。注意两次获得的时钟打点数肯定不相同，即 C1 < C2，并且取值在 [0,107]。

输出格式：

在一行中输出被测函数运行的时间。运行时间必须按照 hh:mm:ss（即2位的 时:分:秒）格式输出；不足 1 秒的时间四舍五入到秒。

输入样例：

123 4577973

输出样例：

12:42:59

#include<stdio.h>
int main() {
	int  c1, c2;
	scanf("%d%d", &c1, &c2);
	int delta = c2 - c1;
	if (delta % 100 >= 50)
		delta = delta / 100 + 1;
	else
		delta = delta / 100;
	
	printf("%02d:%02d:%02d", delta / 3600, delta % 3600 / 60, delta % 60);
	return 0;
}

*3.1 PAT B1046

划拳是古老中国酒文化的一个有趣的组成部分。酒桌上两人划拳的方法为：每人口中喊出一个数字，同时用手比划出一个数字。如果谁比划出的数字正好等于两人喊出的数字之和，谁就赢了，输家罚一杯酒。两人同赢或两人同输则继续下一轮，直到唯一的赢家出现。

下面给出甲、乙两人的划拳记录，请你统计他们最后分别喝了多少杯酒。

输入格式：

输入第一行先给出一个正整数 N（≤100），随后 N 行，每行给出一轮划拳的记录，格式为：

甲喊 甲划 乙喊 乙划

其中喊是喊出的数字，划是划出的数字，均为不超过 100 的正整数（两只手一起划）。

输出格式：

在一行中先后输出甲、乙两人喝酒的杯数，其间以一个空格分隔。

输入样例：

输出样例：

1 2

#include<stdio.h>
int main() {
	int am, ah, bm, bh, n, a = 0, b = 0;
	scanf("%d", &n);
	for (int i = 0; i < n; i++) {
		scanf("%d%d%d%d", &am, &ah, &bm, &bh);
		if (ah == am + bm && bh != am + bm)
			b++;
		if (bh == am + bm && ah != am + bm)
			a++;
	}

	printf("%d %d", a, b);
	return 0;
}

*3.1 PAT B1008

一个数组A中存有N（>0）个整数，在不允许使用另外数组的前提下，将每个整数循环向右移M（≥0）个位置，即将A中的数据由（A0A1⋯A**N−1）变换为（A**N−M⋯A**N−1A0A1⋯A**N−M−1）（最后M个数循环移至最前面的M个位置）。如果需要考虑程序移动数据的次数尽量少，要如何设计移动的方法？

输入格式:

每个输入包含一个测试用例，第1行输入N（1≤N≤100）和M（≥0）；第2行输入N个整数，之间用空格分隔。

输出格式:

在一行中输出循环右移M位以后的整数序列，之间用空格分隔，序列结尾不能有多余空格。

输入样例:

6 2
1 2 3 4 5 6

输出样例:

5 6 1 2 3 4

//算法笔记
int main() {
	int n, m, count = 0;
	int arr[110];
	scanf("%d%d", &n, &m);
	m = m % n;
	for (int i = 0; i < n; i++) {
		scanf("%d", &arr[i]);
	}
	for (int i = n - m; i < n; i++) {
		printf("%d", arr[i]);
		count++;
		if (count < n)printf(" ");
	}
	for (int i = 0; i < n - m; i++) {
		printf("%d", arr[i]);
		count++;
		if (count < n)printf(" ");
	}
	return 0;
}
//三次逆置法
#include<stdio.h>
//逆置
void reverse(int arr[],int low,int high) {
	int temp;
	while (low < high) {
		temp = arr[low];
		arr[low] = arr[high];
		arr[high] = temp;
		low++;
		high--;
	}
}

void main() {
	int arr[110];
	int n, m, count = 0;
	scanf("%d%d", &n, &m);
	m = m % n;
	for (int i = 0; i < n; i++) {
		scanf("%d", &arr[i]);
	}
	//for (int i = 0; i < n; i++) {
	//	printf("%d ", arr[i]);
	//}
	//printf("\n");
	reverse(arr, 0, n - m - 1);
	reverse(arr, n - m, n-1);
	reverse(arr, 0, n-1);
	for (int i = 0; i < n; i++) {
		printf("%d", arr[i]);
		count++;
		if (count < n)printf(" "); 
        //printf("%d ",arr[i]);//注意,最有如果多输出了一个空格,会报格式错误
	}
}

*3.1 PAT B1012

给定一系列正整数，请按要求对数字进行分类，并输出以下 5 个数字：

A1 = 能被 5 整除的数字中所有偶数的和；
A2 = 将被 5 除后余 1 的数字按给出顺序进行交错求和，即计算 n1−n2+n3−n4⋯；
A3 = 被 5 除后余 2 的数字的个数；
A4 = 被 5 除后余 3 的数字的平均数，精确到小数点后 1 位；
A5 = 被 5 除后余 4 的数字中最大数字。

输入格式：

每个输入包含 1 个测试用例。每个测试用例先给出一个不超过 1000 的正整数 N，随后给出 N 个不超过 1000 的待分类的正整数。数字间以空格分隔。

输出格式：

对给定的 N 个正整数，按题目要求计算 A1~A5 并在一行中顺序输出。数字间以空格分隔，但行末不得有多余空格。

若其中某一类数字不存在，则在相应位置输出 N。

输入样例 1：

13 1 2 3 4 5 6 7 8 9 10 20 16 18

输出样例 1：

30 11 2 9.7 9

输入样例 2：

8 1 2 4 5 6 7 9 16

输出样例 2：

N 11 2 N 9

#include<stdio.h>
int main() {
	int n, num;
	scanf("%d", &n);
	int count[5] = {};
	int arr[5] = {};
	int flag = 1;
	for (int i = 0; i < n; i++) {
		scanf("%d", &num);
		//a1
		if (num % 5 == 0 && num % 2 == 0) {
			arr[0] += num;
			count[0]++;
		}
		//a2
		if (num % 5 == 1) {
			if (flag) {
				arr[1] += num;
				count[1]++;
				flag = 0;
			}
			else {
				arr[1] -= num;
				count[1]++;
				flag = 1;
			}
		}
		//a3
		if (num % 5 == 2) {
			arr[2]++;
			count[2]++;
		}
		//a4
		if (num % 5 == 3) {
			arr[3] += num;
			count[3]++;
		}
		//a5
		if (num % 5 == 4) {
			if (num > arr[4]) {
				arr[4] = num;
				count[4]++;
			}
		}
	}
	if (count[0] == 0)
		printf("N");
	else {
		printf("%d", arr[0]);
	}
	printf(" ");
	if (count[1] == 0)
		printf("N");
	else {
		printf("%d", arr[1]);
	}
	printf(" ");
	if (count[2] == 0)
		printf("N");
	else {
		printf("%d", arr[2]);
	}
	printf(" ");
	if (count[3] == 0)
		printf("N");
	else {
		printf("%.1f",(double)arr[3]/ count[3]);
	}
	printf(" ");
	if (count[4] == 0)
		printf("N");
	else {
		printf("%d", arr[4]);
	}
}

*3.1 PAT B1018

大家应该都会玩“锤子剪刀布”的游戏：两人同时给出手势，胜负规则如图所示：

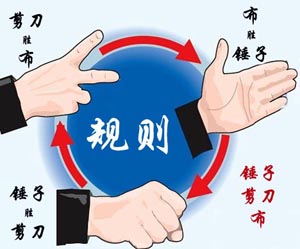
现给出两人的交锋记录，请统计双方的胜、平、负次数，并且给出双方分别出什么手势的胜算最大。

输入格式：

输入第 1 行给出正整数 N（≤105），即双方交锋的次数。随后 N 行，每行给出一次交锋的信息，即甲、乙双方同时给出的的手势。C 代表“锤子”、J 代表“剪刀”、B 代表“布”，第 1 个字母代表甲方，第 2 个代表乙方，中间有 1 个空格。

输出格式：

输出第 1、2 行分别给出甲、乙的胜、平、负次数，数字间以 1 个空格分隔。第 3 行给出两个字母，分别代表甲、乙获胜次数最多的手势，中间有 1 个空格。如果解不唯一，则输出按字母序最小的解。

输入样例：

10
C J
J B
C B
B B
B C
C C
C B
J B
B C
J J

输出样例：

5 3 2
2 3 5
B B

//10分
int main() {

	int n;
	scanf("%d", &n);
	char a, b;
	//count 记录0胜1平2负
	int a_count[3] = {};
	int b_count[3] = {};
	//pose 记录 0锤子C 1剪刀J 2布B
	int a_pose[3] = {};
	int b_pose[3] = {};

	for (int  i = 0; i < n; i++) {
		//用getchar接回车
		getchar();
		scanf("%c %c", &a, &b);
		if (a == 'C') {
			if (b == 'C') {
				a_count[1]++;
				b_count[1]++;
			}
			if (b == 'J') {
				a_count[0]++;
				b_count[2]++;
				a_pose[0]++;
			}
			if (b == 'B') {
				a_count[2]++;
				b_count[0]++;
				b_pose[2]++;
			}
		}
		//pose 记录 锤子C 剪刀J 布B
		if (a == 'J') {
			if (b == 'C') {
				a_count[2]++;
				b_count[0]++;
				b_pose[0]++;
			}
			if (b == 'J') {
				a_count[1]++;
				b_count[1]++;
			}
			if (b == 'B') {
				a_count[0]++;
				b_count[2]++;
				a_pose[1]++;
			}
		}
		//pose 记录 锤子C 剪刀J 布B
		if (a == 'B') {
			if (b == 'C') {
				a_count[0]++;
				b_count[2]++;
				a_pose[2]++;
			}
			if (b == 'J') {
				a_count[2]++;
				b_count[0]++;
				b_pose[1]++;
			}
			if (b == 'B') {
				a_count[1]++;
				b_count[1]++;
			}
		}
		
	}


	printf("%d %d %d\n", a_count[0], a_count[1], a_count[2]);
	printf("%d %d %d\n", b_count[0], b_count[1], b_count[2]);

	int max_a = 0, max_b = 0;
	for (int i = 0; i < 3; i++) {
		if (a_pose[i] > max_a)
			max_a = a_pose[i];
	}
	for (int i = 0; i < 3; i++) {
		if (b_pose[i] > max_b)
			max_b = b_pose[i];
	}

	if (max_a == 2)
		printf("B ");
	else if (max_a == 0)
		printf("C ");
	else if (max_a == 1)
		printf("J ");

	if (max_b == 2)
		printf("B");
	else if (max_b == 0)
		printf("C");
	else if (max_b == 1)
		printf("J");
}
----------------------------------------------------------
    //算法笔记
#include<stdio.h>
int change(char c) {
	if (c == 'B')return 0;
	if (c == 'C')return 1;
	if (c == 'J')return 2;
}

int main() {
	char mp[3] = { 'B','C','J' };
	int n;
	scanf("%d", &n);
	int times_A[3] = { 0 }, times_B[3] = { 0 };
	int hand_A[3] = { 0 }, hand_B[3] = { 0 };
	char c1, c2;
	int k1, k2;
	for (int i = 0; i < n; i++) {
		getchar();
		scanf("%c %c", &c1, &c2);
		k1 = change(c1);
		k2 = change(c2);

		if ((k1 + 1) % 3 == k2) {
			times_A[0]++;
			times_B[2]++;
			hand_A[k1]++;
		}
		else if (k1 == k2) {
			times_A[1]++;
			times_B[1]++;
		}
		else {
			times_A[2]++;
			times_B[0]++;
			hand_B[k2]++;
		}
	}
	printf("%d %d %d\n", times_A[0], times_A[1], times_A[2]);
	printf("%d %d %d\n", times_B[0], times_B[1], times_B[2]);
	int id1 = 0, id2 = 0;
	for (int i = 0; i < 3; i++) {
		if (hand_A[i] > hand_A[id1])id1 = i;
		if (hand_B[i] > hand_B[id2])id2 = i;
	}
	printf("%c %c\n", mp[id1], mp[id2]);
	return 0;
}

*3.1 PAT A1042

Shuffling is a procedure used to randomize a deck of playing cards. Because standard shuffling techniques are seen as weak, and in order to avoid “inside jobs” where employees collaborate with gamblers by performing inadequate shuffles, many casinos employ automatic shuffling machines. Your task is to simulate a shuffling machine.

The machine shuffles a deck of 54 cards according to a given random order and repeats for a given number of times. It is assumed that the initial status of a card deck is in the following order:

S1, S2, ..., S13, 
H1, H2, ..., H13, 
C1, C2, ..., C13, 
D1, D2, ..., D13, 
J1, J2

where “S” stands for “Spade”, “H” for “Heart”, “C” for “Club”, “D” for “Diamond”, and “J” for “Joker”. A given order is a permutation of distinct integers in [1, 54]. If the number at the i-th position is j, it means to move the card from position i to position j. For example, suppose we only have 5 cards: S3, H5, C1, D13 and J2. Given a shuffling order {4, 2, 5, 3, 1}, the result will be: J2, H5, D13, S3, C1. If we are to repeat the shuffling again, the result will be: C1, H5, S3, J2, D13.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer K (≤20) which is the number of repeat times. Then the next line contains the given order. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the shuffling results in one line. All the cards are separated by a space, and there must be no extra space at the end of the line.

Sample Input:

2
36 52 37 38 3 39 40 53 54 41 11 12 13 42 43 44 2 4 23 24 25 26 27 6 7 8 48 49 50 51 9 10 14 15 16 5 17 18 19 1 20 21 22 28 29 30 31 32 33 34 35 45 46 47

Sample Output:

S7 C11 C10 C12 S1 H7 H8 H9 D8 D9 S11 S12 S13 D10 D11 D12 S3 S4 S6 S10 H1 H2 C13 D2 D3 D4 H6 H3 D13 J1 J2 C1 C2 C3 C4 D1 S5 H5 H11 H12 C6 C7 C8 C9 S2 S8 S9 H10 D5 D6 D7 H4 H13 C5

#include<stdio.h>
const int N = 54;
int main() {
	int K;
	scanf("%d", &K);
	int start[55], end[55], next[55];
	for (int i = 1; i <= N; i++) {
		start[i] = i;
	}
	for (int i = 1; i <= N; i++) {
		scanf("%d", &next[i]);
	}
	for (int step = 0; step < K; step++) {
		for (int i = 1; i <= N; i++) {
			end[next[i]] = start[i];
		}
		for (int i = 1; i <= N; i++) {
			start[i] = end[i];
		}
	}

	char color[5] = { 'S','H','C','D','J' };

	for (int i = 1; i <= N; i++) {
		if (i != 1)printf(" ");
		start[i]--;
		printf("%c%d", color[start[i] / 13], start[i] % 13 + 1);
		//if (i != 54)
		//	printf(" ");
	}
	return 0;
}

*3.1 PAT A1046

The task is really simple: given N exits on a highway which forms a simple cycle, you are supposed to tell the shortest distance between any pair of exits.

Input Specification:

Each input file contains one test case. For each case, the first line contains an integer N (in [3,105]), followed by N integer distances D1 D2 ⋯ D**N, where D**i is the distance between the i-th and the (i+1)-st exits, and D**N is between the N-th and the 1st exits. All the numbers in a line are separated by a space. The second line gives a positive integer M (≤104), with M lines follow, each contains a pair of exit numbers, provided that the exits are numbered from 1 to N. It is guaranteed that the total round trip distance is no more than 107.

Output Specification:

For each test case, print your results in M lines, each contains the shortest distance between the corresponding given pair of exits.

Sample Input:

5 1 2 4 14 9
3
1 3
2 5
4 1

Sample Output:

3
10
7

#include<stdio.h>
#include<algorithm>
using namespace std;
const int MAXN = 100005;
int dis[MAXN], A[MAXN];
int main() {
	int sum = 0, query, n, left, right;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%d", &A[i]);
		sum += A[i];
		dis[i] = sum;
	}
	scanf("%d", &query);
	for (int i = 0; i < query; i++) {
		scanf("%d%d", &left, &right);
		if (left > right)swap(left, right);
		int temp = dis[right - 1] - dis[left - 1];//右侧减去左侧
		printf("%d\n", min(temp, sum - temp));//从左边和从右边找最小的路径
	}
	return 0;
}

*3.1 PAT A1065

Given three integers A, B and C in (−263,263), you are supposed to tell whether A+B>C.

Input Specification:

The first line of the input gives the positive number of test cases, T (≤10). Then T test cases follow, each consists of a single line containing three integers A, B and C, separated by single spaces.

Output Specification:

For each test case, output in one line Case #X: true if A+B>C, or Case #X: false otherwise, where X is the case number (starting from 1).

Sample Input:

3
1 2 3
2 3 4
9223372036854775807 -9223372036854775808 0

Sample Output:

Case #1: false
Case #2: true
Case #3: false

#include<stdio.h>
int main() {
	int n;
	long long a, b, c, res;
	int flag;
	scanf("%d", &n);
	for (int i = 0; i < n; i++) {
		scanf("%lld%lld%lld", &a, &b, &c);
		res = a + b;
		if (a > 0 && b > 0 && res < 0) {
			flag = 1;
		}
		else if (a < 0 && b < 0 && res >= 0) {
			flag = 0;
		}
		else if (res > c) {
			flag = 1;
		}
		else {
			flag = 0;
		}
		if (flag == 1) {
			printf("Case #%d: true\n", i + 1);
		}
		else {
			printf("Case #%d: false\n", i + 1);
		}
	}
	return 0;
}

*3.1 PAT B1010

设计函数求一元多项式的导数。（注：x**n（n为整数）的一阶导数为nxn−1。）

输入格式:

以指数递降方式输入多项式非零项系数和指数（绝对值均为不超过 1000 的整数）。数字间以空格分隔。

输出格式:

以与输入相同的格式输出导数多项式非零项的系数和指数。数字间以空格分隔，但结尾不能有多余空格。注意“零多项式”的指数和系数都是 0，但是表示为 0 0。

输入样例:

3 4 -5 2 6 1 -2 0

输出样例:

12 3 -10 1 6 0

#include<stdio.h>
int main() {
	int a[1010] = { 0 };
	int k, e, count = 0;
	while (scanf("%d%d", &k, &e) != EOF) {
		a[e] = k;
	}
	a[0] = 0;
	for (int i = 1; i <= 1000; i++) {
		a[i - 1] = a[i] * i;
		a[i] = 0;
		if (a[i - 1] != 0)count++;
	}
	if (count == 0)printf("0 0");
	else {
		for (int i = 1000; i >= 0; i--) {
			if (a[i] != 0) {
				printf("%d %d", a[i], i);
				count--;
				if (count != 0)printf(" ");
			}
		}
	}
	return 0;
}

*3.1 PAT A1002

This time, you are supposed to find A+B where A and B are two polynomials.

Input Specification:

Each input file contains one test case. Each case occupies 2 lines, and each line contains the information of a polynomial:

K N1 a**N1 N2 a**N2 … N**K aNK

where K is the number of nonzero terms in the polynomial, N**i and aNi (i=1,2,⋯,K) are the exponents(幂) and coefficients(系数), respectively. It is given that 1≤K≤10，0≤N**K<⋯<N2<N1≤1000.

Output Specification:

For each test case you should output the sum of A and B in one line, with the same format as the input. Notice that there must be NO extra space at the end of each line. Please be accurate to 1 decimal place.

Sample Input:

2 1 2.4 0 3.2
2 2 1.5 1 0.5

Sample Output:

3 2 1.5 1 2.9 0 3.2

#include<stdio.h>
int main() {
	double p[1010] = {};
	int k, n, count = 0;
	double a;
	scanf("%d", &k);
	for (int i = 0; i < k; i++) {
		scanf("%d %lf", &n, &a);
		p[n] += a;
	}
	scanf("%d", &k);
	for (int i = 0; i < k; i++) {
		scanf("%d %lf", &n, &a);
		p[n] += a;
	}
	for (int i = 0; i < 1010; i++) {
		if (p[i] != 0) {
			count++;
		}
	}
	printf("%d", count);
	for (int i = 1009; i >= 0; i--) {
		if (p[i] != 0) {
			printf(" %d %.1f", i, p[i]);
		}
	}
	return 0;
}

*3.1 PAT A1009

This time, you are supposed to find A×B where A and B are two polynomials.

Input Specification:

Each input file contains one test case. Each case occupies 2 lines, and each line contains the information of a polynomial:

K N1 a**N1 N2 a**N2 … N**K aNK

where K is the number of nonzero terms in the polynomial, N**i and aNi (i=1,2,⋯,K) are the exponents and coefficients, respectively. It is given that 1≤K≤10, 0≤N**K<⋯<N2<N1≤1000.

Output Specification:

For each test case you should output the product of A and B in one line, with the same format as the input. Notice that there must be NO extra space at the end of each line. Please be accurate up to 1 decimal place.

Sample Input:

2 1 2.4 0 3.2
2 2 1.5 1 0.5

Sample Output:

3 3 3.6 2 6.0 1 1.6

#include<stdio.h>
struct Poly {
	int exp;
	double cof;
}poly[1001];

double ans[2001];

int main() {
	int n, m, number = 0;
	scanf("%d", &n);
	for (int i = 0; i < n; i++) {
		scanf("%d %lf", &poly[i].exp, &poly[i].cof);
	}
	scanf("%d", &m);
	int exp;
	double cof;
	for (int i = 0; i < m; i++) {
		scanf("%d %lf", &exp, &cof);
		for (int j = 0; j < n; j++) {
			ans[exp + poly[j].exp] += cof * poly[j].cof;
		}
	}

	for (int i = 0; i <= 2000; i++) {
		if (ans[i] != 0.0)
			number++;
	}
	printf("%d", number);
	for (int i = 2000; i >= 0; i--) {
		if (ans[i] != 0.0) {
			printf(" %d %.1f", i, ans[i]);
		}
	}
	return 0;

}