【剑指 Offer 36. 二叉搜索树与双向链表】

• 中序遍历
• 有序循环双向链表

题目描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

为了让您更好地理解问题，以下面的二叉搜索树为例：

我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

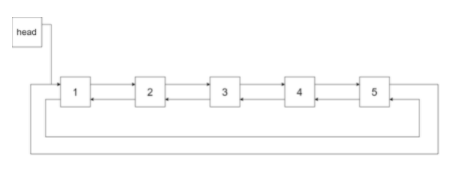
特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

解题思路

二叉搜索树的中序遍历是递增的，我们可以在中序遍历中添加前驱和后继指针，就可以构成有序循环链表。

一颗二叉搜索树BST如图所示：

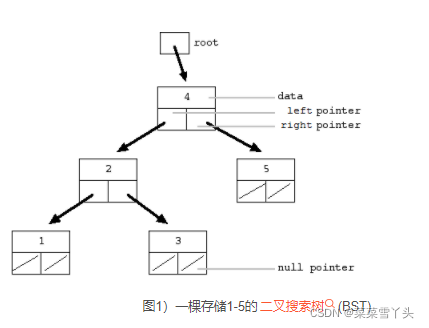
根据上面的BST转换得到的有序循环链表。其中，树的左右孩子指针替换成了pre和next指针，分别指向链表的前一个和后一个结点。

代码

class Solution {
    Node pre, head;
    public Node treeToDoublyList(Node root) {
        if(root == null) return null;
        //执行中序遍历（因为是二叉搜索树，所以可得到递增的排序）
        dfs(root);
        //完成中序遍历后，补充尾节点和头节点的前驱后继关系
        head.left = pre;
        pre.right = head;
        //返回排序的双向循环链表
        return head;   
    }

    void dfs(Node cur){
        if(cur == null) return;

        //前
        dfs(cur.left);

        //中（此时为中序遍历的各个值，可对其进行操作）
        if(pre == null) head = cur; //因为pre为空时head=cur，此时的cur=1，所以head一直是1，而cur时中序遍历的结果：1，2，3，4，5
        else{
            pre.right = cur;
            cur.left = pre;
        }
        pre = cur; 
        
        //后
        dfs(cur.right);
    }
}

复杂度分析

• 时间复杂度 O(N) ： N 为二叉树的节点数，中序遍历需要访问所有节点。
• 空间复杂度 O(N) ： 最差情况下，即树退化为链表时，递归深度达到 N，系统使用 O(N) 栈空间。