感知算法工程师

参考链接

一、深度学习

面经汇总

1. 面试题汇总1-掘金
2. 面试题汇总2-知乎
3. 知识点总结1-掘金
4. 知识点总结2-吴恩达

1、优化算法

1.1梯度下降算法推导

1.2 EMA算法（指数移动平均）

（1）概念：类似于加权平均，只不过权重右后往前进行指数衰减；
（2）计算：以计算平均温度为例，计算前t天的温度，可以由前（t-1）天的平均值和第t天的温度计算得到；
（3）优点：通过递推公式进行计算，只需要保存当前数据和之前的平均数，适合于深度学习的大规模数据处理。
（4）偏差修正：当默认v0 = 0时，会导致初始vt不够准确，因此可以通过除以（1-β^{t）进行修正，当t很大时，1-β}t ≈ 1 ，即基本不再进行修正

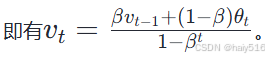
1.3 Momentum（动量梯度下降）

（1）概念：在每次迭代过程中，计算梯度的指数加权平均数，并使用该值进行更新权重W和b
（2）作用：使用之前的梯度进行更新参数，可以加快收敛速度
（3）理解：比如在某一个维度dw方向不同，波动较大，通过计算指数加权平均，可以进行正负抵消，较少波动；而对于某一维度，dw的方向相同，通过计算指数加权平均，可以进行梯度叠加，加快参数更新减小收敛过程中的波动后，便可使用较大的学习率进行更新参数，加快训练过程。

实现过程如下：

可视化效果对比：

1.4 RMSProp算法（均方根传播）

（1）概念：修改指数加权平均的计算公式，引入平方和开方。公式如下：
（2）作用：减小某些维度的波动，加快收敛速度


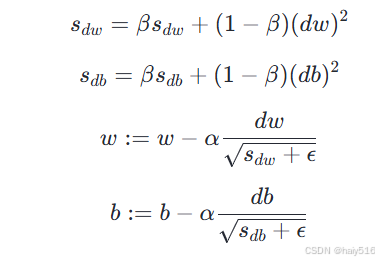
理解：

1.4 Adam 优化算法

概念：将Momentum算法和RMSProp进行结合

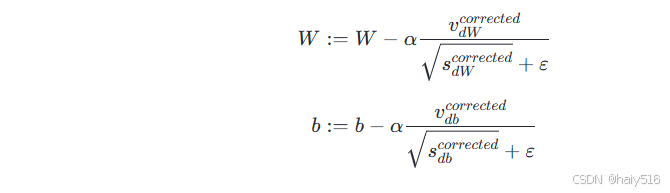
2、经典神经网络

2.1 ResNet

  Resnet是为了解决网络退化问题（即随着网络深度的增加，网络效果反而变差），采样残差结构，以此来加深网络的深度。

3、模型调优

3.1 正则化

3.1.1 正则化缓解过拟合原因

原因：
理解一：缓解过拟合的原理是让模型尽可能简单，也就是让模型的参数尽可能小，甚至为0，而正则化通过对模型权重添加惩罚项，可以时权重变小，L1正则化可以使很多参数为0，因此模型变得更加简单，不容易产生过拟合；
理解二：通过添加正则项，使得参数变小，进而模型得到的输出z值也会变小，对于一些激活函数，如tanh激活函数，在原点附近，激活函数近似为线性激活，因此对于整个网络，更加近似为线性映射，模型也更加简单。

3.1.2 L1正则化

（1）表达式：损失函数中添加权重的L1范数，即各个权重绝对值之和，L1正则化可以产生稀疏解，可以进行特征选择。
（2）产生稀疏解的原因：
理解一：L1正则化对每一个参数，添加相等程度的惩罚，这会导致较小的参数更加趋向于0，导致产生稀疏解；
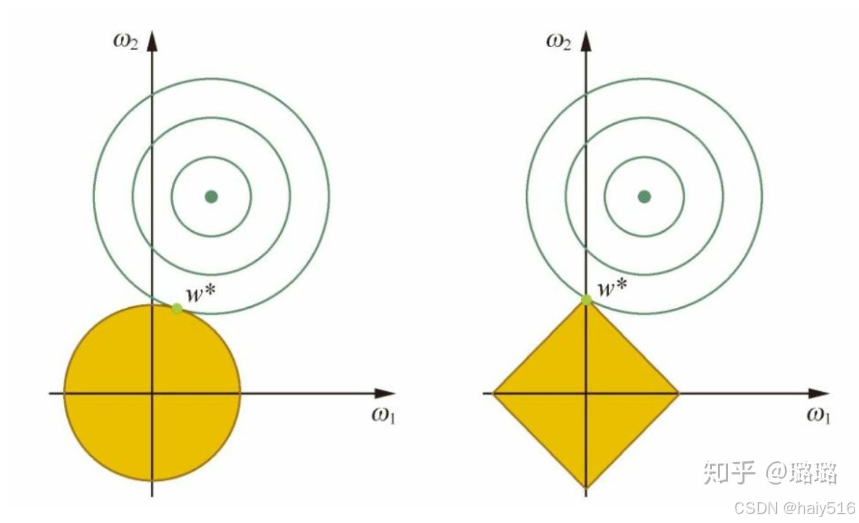
理解二：添加L1正则化后的最优化问题，可以等价于带有条件约束的最优化问题（因为带有约束条件的最优化问题，通过构造拉格朗日函数后解空间与原问题相同）。从解的可行域来看，L1的正则项函数解的可行域具有更多棱角，更容易与损失函数解的可行域在坐标轴产生交点，从而产生更多的稀疏解。

3.1.2 L2正则化

（1）表达式：损失函数中添加权重L2范数的平方，即各个权重平方之和

3.2 Dropout

（1）概念：在进行训练时，随机将某些神经元删除，以此训练一个更小的神经网络；
（2）操作：以反向随机失活 (Inverted Dropout)为例：
keep_prob = 0.8 # 设置神经元保留概率
dl = np.random.rand (al.shape[0], al.shape[1]) < keep_prob #产生一个mask
al = np.multiply (al, dl) #使用mask对al进行删除
al /= keep_prob #为了保持al的期望，这样在进行推理时，就不需要进行dropout操作
（3）缓解过拟合理解：
理解一：对于整个网络来说，dropout后，每次训练时，相当于训练一个小的网络，网络结构更加简单；
理解二：对于单个神经元，该神经元的输入，在每次进行训练时，某些输入会被随机删除，
因此，对于每一个输入，都会倾向于给予一个更小的权重。这样整个网络的权重就会更小，
得到类似于正则化的效果。
（4）keep_prob 参数设置：参数量多的层，更加容易出现过拟合，设置更小的keep_prob
（5）缺点：损失函数无法被明确定义，因为每次迭代时都会删除一些神经元的影响，无法保证损失收敛；
因此，在使用dropout之前，先确定一下模型的损失是否正常收敛。

3.3 Batch Normalization

3.3.1 标准化输入

（1）概念：对输入进行归一化处理，即先计算输入数据的均值和标准差，
将输入数据减去均值，再除以标准差
（2）作用：加快模型收敛速度，减少随机初始化对训练过程的影响。
（3）理解：
归一化输入后，可以将数据范围统一到相同的尺度，避免了数据在不同维度下差异较大的问题，
有利于梯度下降算法的进行，且较小了随机初始化对训练的影响

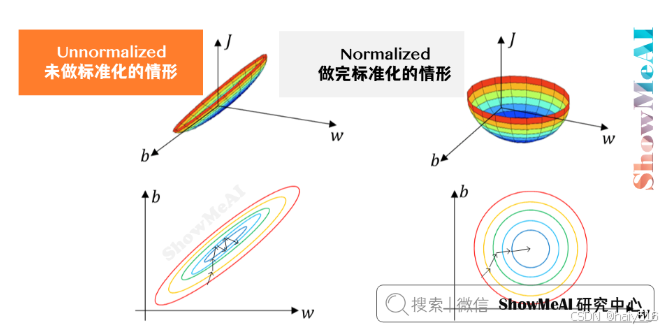
3.3.2 BN层-训练过程

（1）概念：对每一个隐藏层的z值（激活函数之前），进行标准化处理，以此加快网络训练速度，
类似于标准化输入
（2）作用：加快模型训练速度（原因见标准化输入）；一定的正则化作用，理解：
BN层是使用一个batch数据计算的均值和方差，因此具有一定噪声，这种噪声会起到类似dropout的作用；
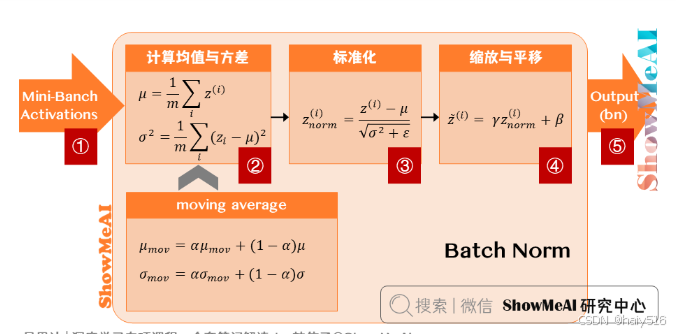
（3）具体实现：
a) 均值/方差的计算：是以通道为单位进行计算的，
就是在一个批次内，将每个通道中的数字单独加起来，再除以NHW，其中N是batchsize，W,H为尺寸大小，
计算得到的均值和方差维度等于通道数
b) 可训练参数γ、β：对归一化的数据进行平移和缩放变换，维度也等于通道数，
网络的每一层都有该层对应的γ、β，维度等于该层的通道数
c) 在训练时，通过EMA算法计算γ、β的指数加权平均数，作为测试时的均值和方差。

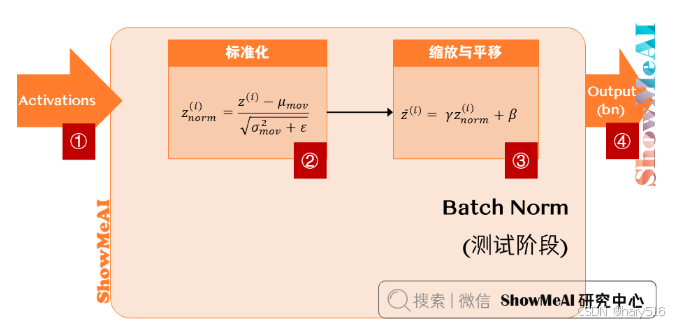
3.3.3 BN层-测试过程

使用训练时计算的γ、β的指数加权平均数，进行归一化处理。
原因：训练时计算的是一个batchsize数据的均值和方差，在测试时通常是对单个样本进行处理，而计算单个样本的均值和方差没有意义。

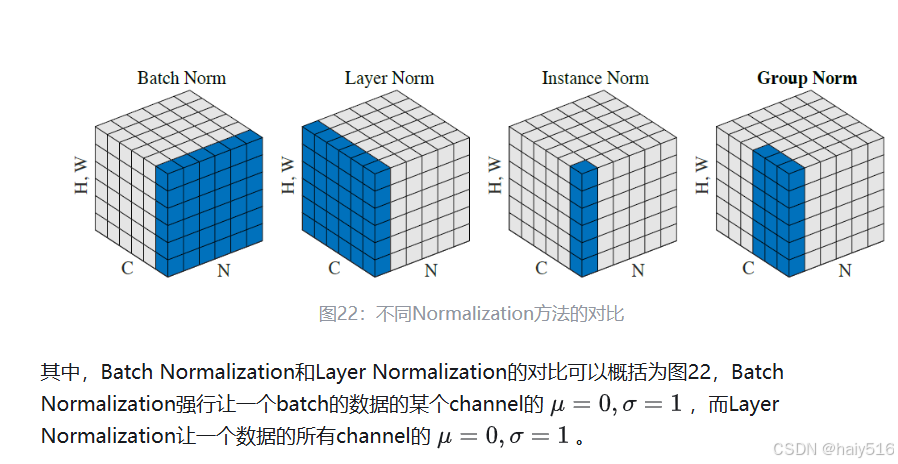
3.3.4 Batch Normalization和Layer Normalization

4、损失函数

4.1 iou损失函数

Smooth L1 Loss-> IoU Loss（2016）-> GIoU Loss（2019）-> DIoU Loss（2020）->CIoU Loss（2020）

1、iou loss问题：
（1）无法处理框不想交的情况（iou=0）
（2）当iou相同时，无法进行区分好坏
2、Ciou Loss
（1）计算iou时，需要考虑三个方面，分别是重叠面积、中心距离、宽高比，Ciou Loss将其全部进行考虑

二、目标检测

目标检测面经

1. 目标检测面经1-知乎
2. 目标检测知识点1-掘金

1、2D目标检测

1.1 YOLO目标检测算法

1.1.1YOLO-v1

参考链接
（1）网络结构：借鉴GoogleNet，24个卷积网络+两个全连接层
（2）预测阶段：输入448448，输出7730, 30=20cats+52（x,y,w,h,c）*2

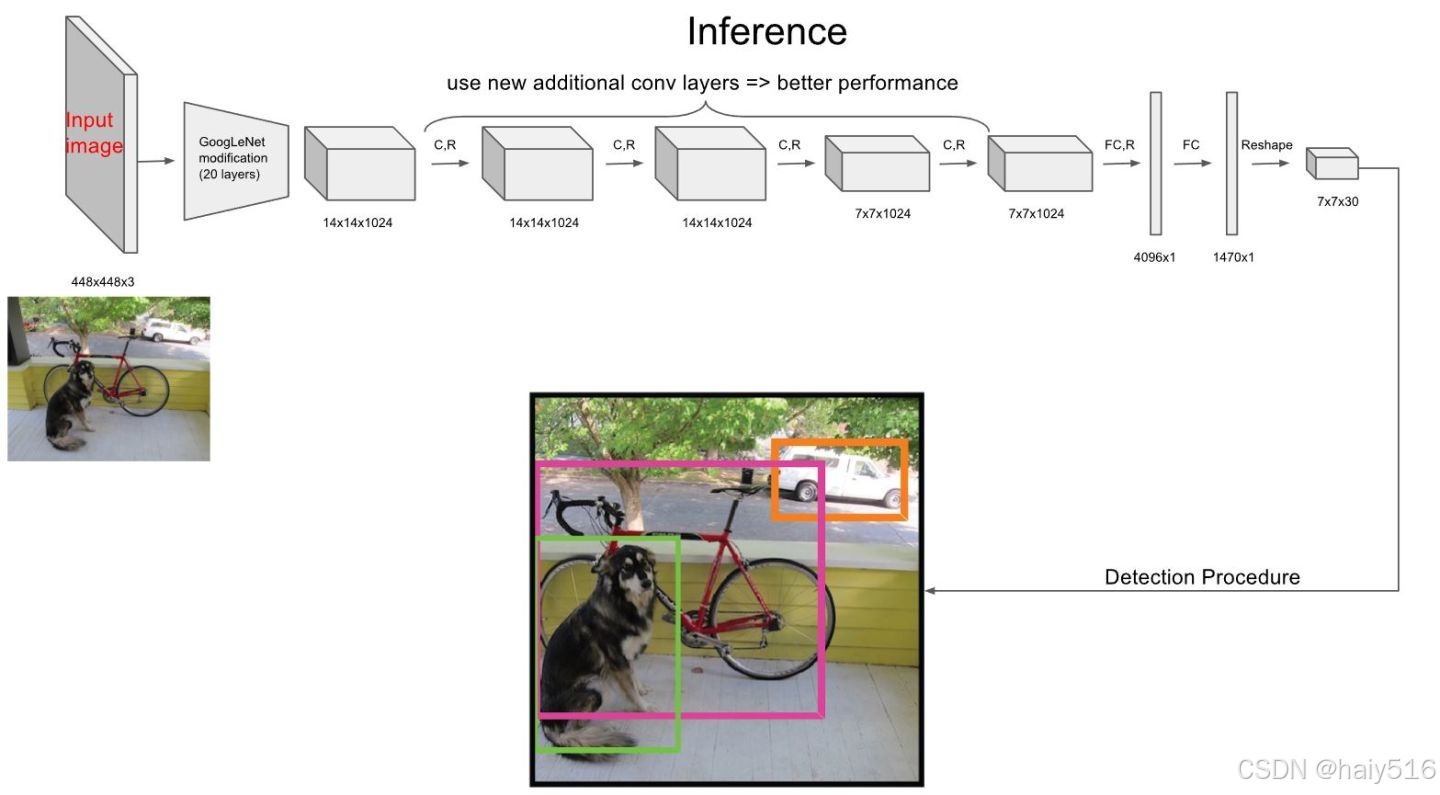
（3）训练阶段：

1. 模型输出为7730，训练时根据模型结果与gt，得到7730个gt，再进行损失计算
2. 一个grid cell会得到2个预测框，选取与gt框最大的作为正例，另一个作为负例
3. x,y,w,h是相对值，范围0-1，其中，x，y坐标是基于每个grid cell的相对坐标，w，h是相对于原图的比例
4. 损失函数
   

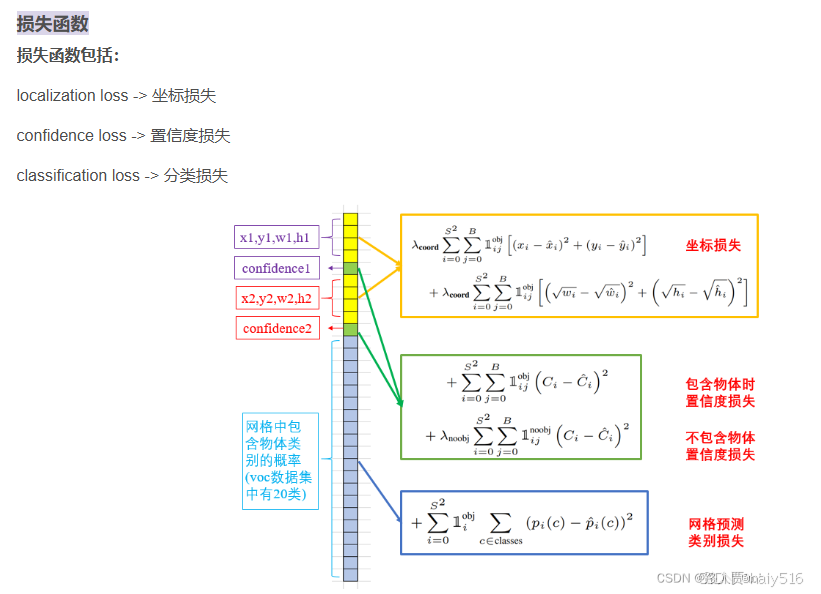
  （4）不足：一个grid cell只能预测一个目标，所以容易出现漏检

1.1.5YOLO-x

标签匹配：
1、初步筛选：
1.1 在所有预测结果中，选出中心点位于gt内部的所有结果
1.2 在所有预测结果中，选出中心点位于gt中心点附近的所有结果。gt中心点附近是指以gt中心点为中心，边长为stride2.52的正方形内。
2、SimOTA
2.1 提取初步筛选出的所有样本
2.2 计算loss与cost
2.3 simOTA求解
2.3.1 选出与每个gtiou最大的10个框，根据iou值求和再clamp，得到该gt要分配的预测框个数
2.3.2 根据cost，将cost低的分配给每个gt，一个gt可能得到多个预测结果
2.3.3 进行去重，排除一个预测结果匹配多个gt
深入浅出Yolo系列之Yolox核心基础完整讲解

1.2 CenterNet

经典的目标检测算法：CenterNet
睿智的目标检测46——Pytorch搭建自己的Centernet目标检测平台

1.2.1介绍

1、基于CornerNet进行的优化，将角点预测改为中心点预测；

CornerNet缺点：
（1）目标框的角点一般都落在语义信息之外，不利于学习，而中心点都位于语义信息之内；
（2）CornerNet需要对角点（左上角右下角）进行配对，降低了算法的性能和效率。
2、省去了anchor机制，提升检测速度；
3、直接在heatmap上面执行了maxpooling操作，在理论上去掉了耗时的NMS后处理操作。

1.2.2原理

1.3 FCOS

1.4 Transformer

参考链接.

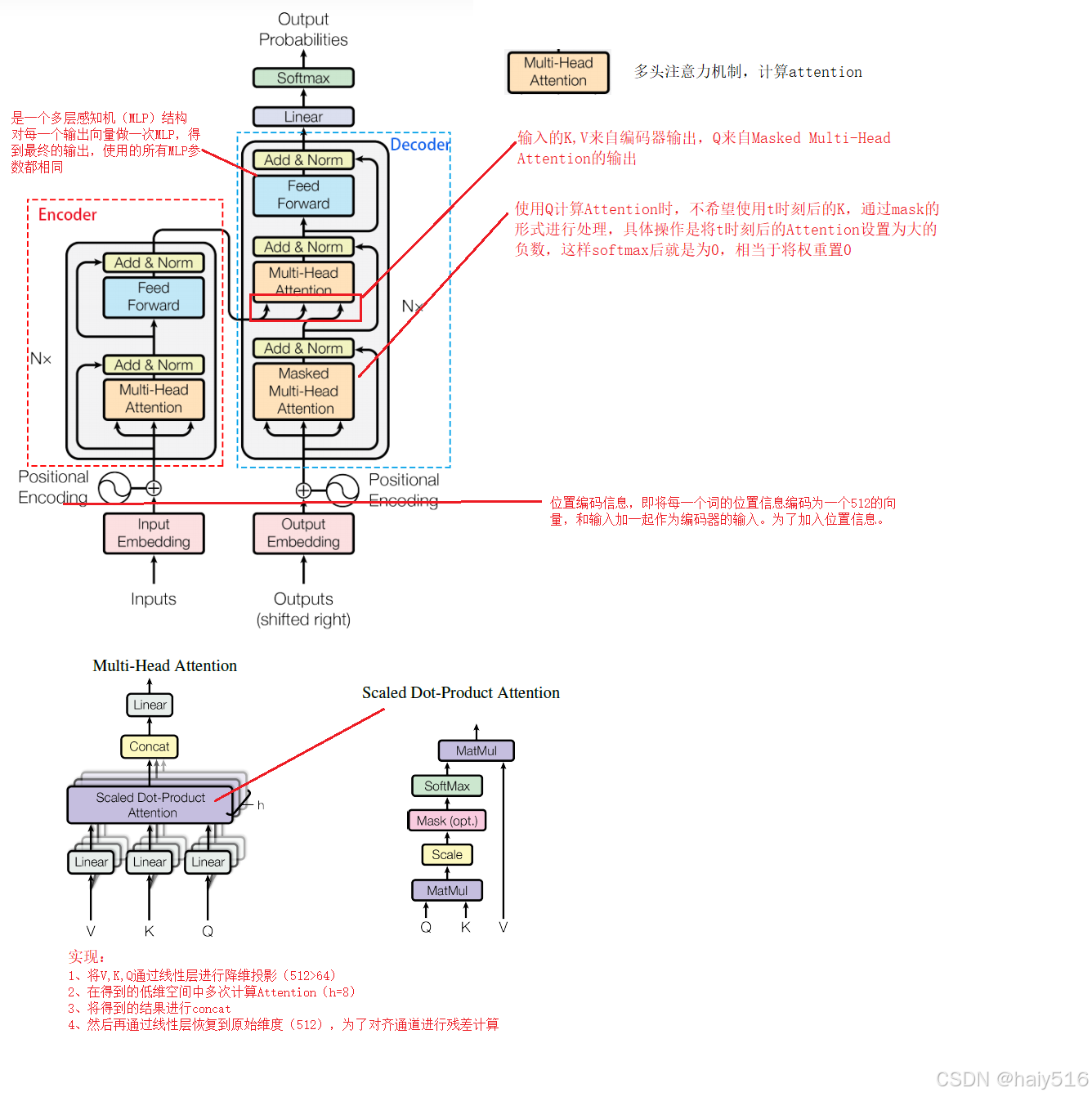
1.4.1 self-Attention

1、input = I（embedding）
2、Q = I * Wq; K = I * Wk; V = I * Wv

$$selfAttention=softmax(\frac{Q\bullet K^T}{\sqrt{d}})\bullet V$$
其中：
$$Q\bullet K^T表示不同输入向量之间的相关性$$
$$softmax(\frac{Q\bullet K^T}{\sqrt{d}})\bullet V相当于加权求和，即给每一个输入向量添加一个权重$$
注：除以根号d的作用：如果当d比较大时 Q与K计算出来的attention值差异比较大时，softmax函数输出会比较陡峭，会导致梯度较小，难以训练，因此做一个平滑处理，使得softmax函数的结果更加平滑。

1.4.2 transformer结构

2、3D目标检测

3、轻量化backbone

3.1 mobileNet

  参考链接
（1）mobileNet-v1
  概念： 把VGG中的标准卷积层换成深度可分离卷积+1x1卷积
  作用：通过深度可分离卷积可以极大减少参数量和计算量（约1/9）
  使用relu6激活函数：将输出限定在6以下，适应低浮点数的表示精度（即低浮点数不能表示太大的数）
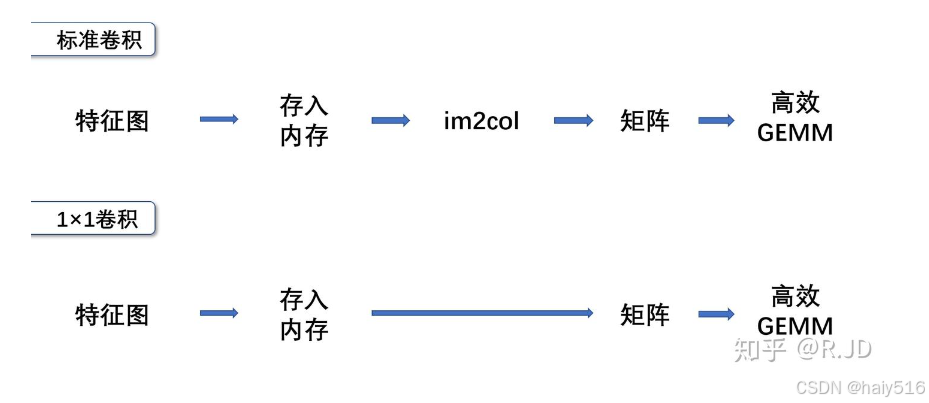
  性能优化原理：结构中95%的计算量来自1x1卷积，而1x1卷积容易优化。

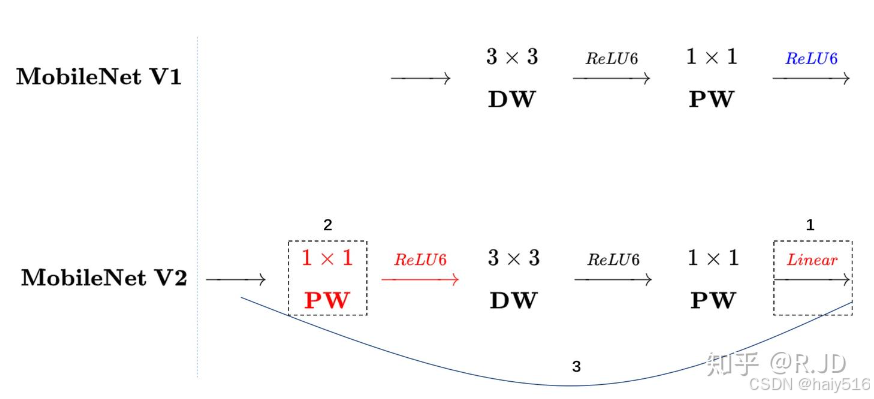
（2）mobileNet-v2
  a) 先使用1x1卷积升维，再进行深度可分离卷积，再使用1x1卷积降维
  b) 降维卷积后加线性激活函数，为了解决v1版本中深度可分离卷积训练后大部分卷积核参数都是0的问题
  c) 添加残差结构

3.2 shuffleNet

参考链接
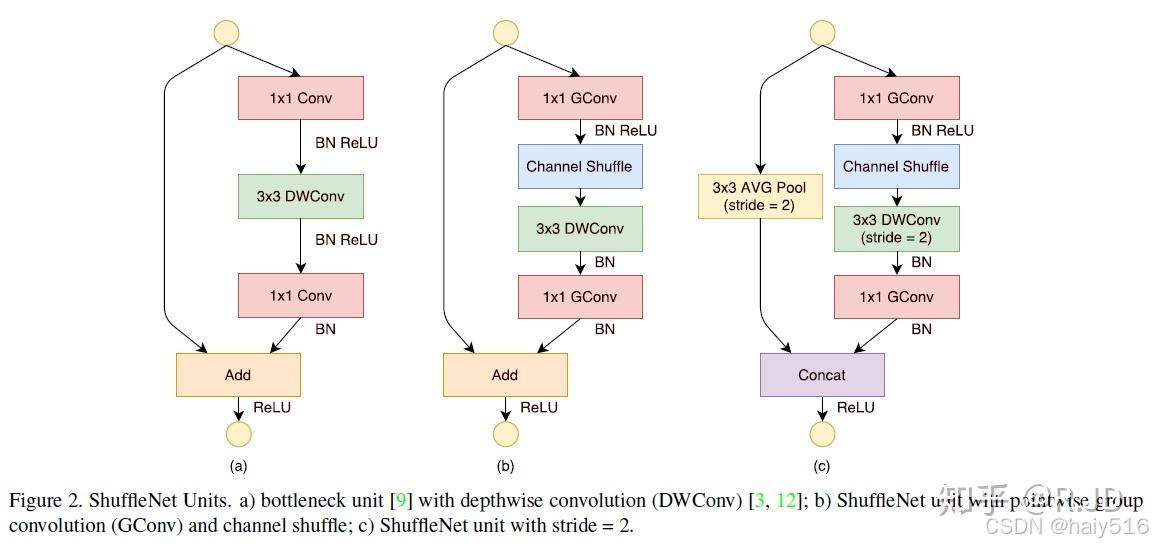
（1）shuffleNet-v1：在ResNet基础上进行改进，改进点为：
  a) 将1x1卷积改为1x1分组卷积，减少1x1卷积的参数量和计算量
   b) 将3x3卷积改为3x3深度可分离卷积，参考mobileNet
  c) 1x1分组卷积后添加channel shuffle层，进行通道重排

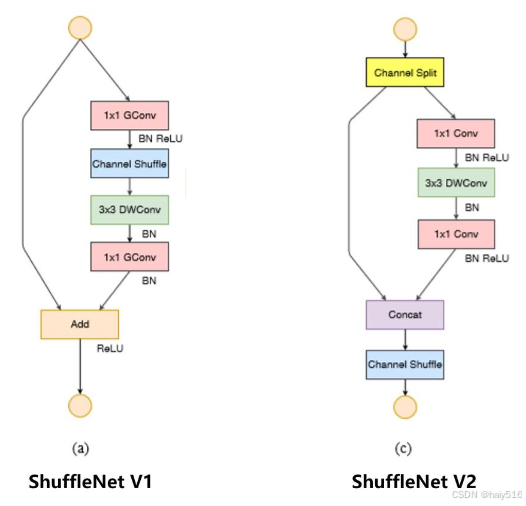
（2）shuffleNet-v2：通过提出的四个网络设计原则，对v1进行优化
  a) 卷积层使用相同的输入输出通道数。
  b) 注意到使用大的分组数所带来的坏处。
  c) 减少分支以及所包含的基本单元。
  d) 减少Element-wise操作。
优化点：
  使用channel split，保证输入输出通道相同
  1x1卷积不采用分组卷积
  进入残差时使用concat取代add

3.3 efficientNet

4、模型优化

4.1、2D检测优化

4.1.1、正负样本匹配与样本均衡

（1）常见检测算法正负样本匹配策略总结
（2）目标检测核心之正负样本匹配与均衡问题

4.1.2、特征融合

（1）BiFPN

4.1.3、损失函数

4.1.4、主干使用elan结构(yolov7)，elan结构

4.2、3D检测优化

4.3、知识蒸馏

概述：主要进行模型轻量化压缩，模型压缩方式总结：
1、压缩已训练好的模型：知识蒸馏、权值量化、权重剪枝、通道剪枝、注意力迁移
2、直接训练轻量化网络：SqueezeNet、MobileNetv1v2v3、MnasNet、SHhffleNet、Xception、EfficientNet、	EfficieentDet
3、加速卷积运算：im2col+GEMM、Wiongrad、低秩分解
4、硬件部署：TensorRT、Jetson、TensorFlow-Slim、openvino、FPGA集成电路

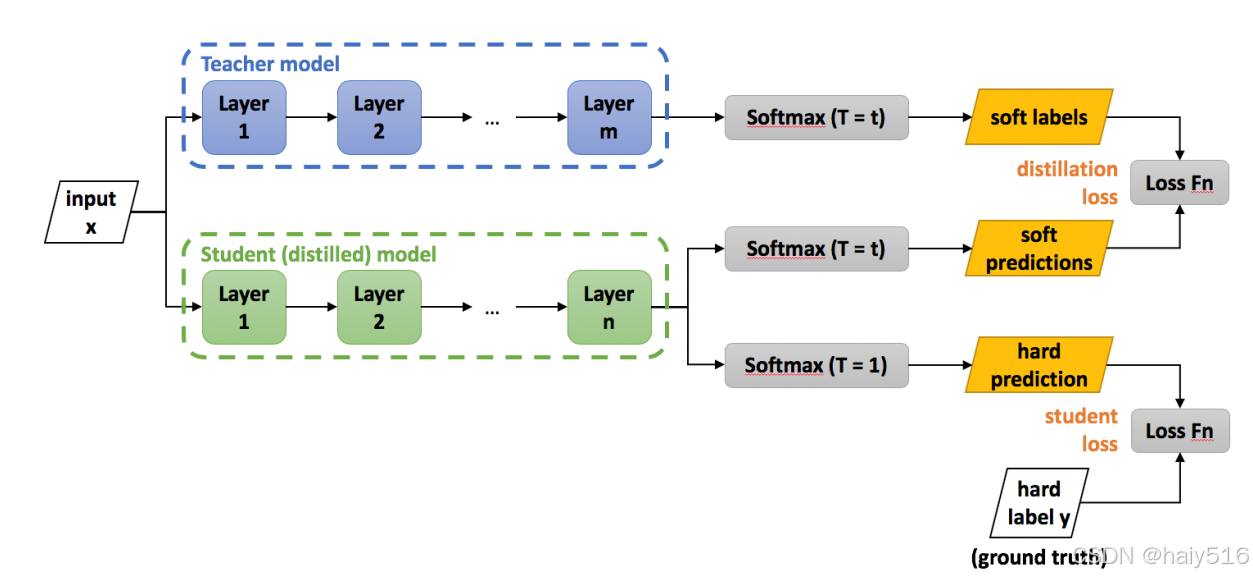
4.3.1、Logits蒸馏（目标蒸馏）

参考链接
（1）直接对分类模型的输出概率分布进行学习
（2）使用温度系数T来控制soft label的分布，学生模型较小，一般采用较低的温度系数，因为参数量小的模型不适合学习太复杂的知识

4.3.2、特征蒸馏

  它不像Logits方法那样，Student只学习Teacher的Logits这种结果知识，而是学习Teacher网络结构中的中间层特征。它强迫Student某些中间层的网络响应，要去逼近Teacher对应的中间层的网络响应。这种情况下，Teacher中间特征层的响应，就是传递给Student的知识，本质是Teacher将特征级知识迁移给Student。

4.3.3、定位蒸馏（目标检测）

5、MMdetection

5.1 MMDetection框架入门教程

三、Python

python面经

1. python面经1-知乎

3.1

四、code

4.1 向量化实现iou

def calculate_iou_multiple(boxes_a, boxes_b):
    # boxes_a 和 boxes_b 是形状为 (N, 4) 的数组
    x1_inter = np.maximum(boxes_a[:, 0, np.newaxis], boxes_b[:, 0])
    y1_inter = np.maximum(boxes_a[:, 1, np.newaxis], boxes_b[:, 1])
    x2_inter = np.minimum(boxes_a[:, 2, np.newaxis], boxes_b[:, 2])
    y2_inter = np.minimum(boxes_a[:, 3, np.newaxis], boxes_b[:, 3])
    
    inter_width = np.maximum(0, x2_inter - x1_inter)
    inter_height = np.maximum(0, y2_inter - y1_inter)
    inter_area = inter_width * inter_height

    area_a = (boxes_a[:, 2] - boxes_a[:, 0]) * (boxes_a[:, 3] - boxes_a[:, 1])
    area_b = (boxes_b[:, 2] - boxes_b[:, 0]) * (boxes_b[:, 3] - boxes_b[:, 1])

    union_area = area_a[:, np.newaxis] + area_b - inter_area

    iou = inter_area / union_area
    return iou

4.2 nms

def calculate_iou(box_a, box_b):
    # 计算交集的左上角和右下角
    x1_inter = np.maximum(box_a[0], box_b[0])
    y1_inter = np.maximum(box_a[1], box_b[1])
    x2_inter = np.minimum(box_a[2], box_b[2])
    y2_inter = np.minimum(box_a[3], box_b[3])
    
    # 计算交集的面积
    inter_width = np.maximum(0, x2_inter - x1_inter)
    inter_height = np.maximum(0, y2_inter - y1_inter)
    inter_area = inter_width * inter_height

    # 计算两个框的面积
    area_a = (box_a[2] - box_a[0]) * (box_a[3] - box_a[1])
    area_b = (box_b[2] - box_b[0]) * (box_b[3] - box_b[1])

    # 计算并集的面积
    union_area = area_a + area_b - inter_area

    # 计算 IoU
    iou = inter_area / union_area
    return iou

def nms(boxes, scores, iou_threshold=0.5):
    # 按得分从高到低排序
    indices = np.argsort(scores)[::-1]
    selected_indices = []

    while len(indices) > 0:
        # 选择得分最高的框
        current_index = indices[0]
        selected_indices.append(current_index)

        # 计算与当前框的 IoU
        current_box = boxes[current_index]
        remaining_boxes = boxes[indices[1:]]
        ious = np.array([calculate_iou(current_box, box) for box in remaining_boxes])

        # 只保留 IoU 小于阈值的框
        indices = indices[np.where(ious <= iou_threshold)[0] + 1]

    return selected_indices