吴恩达机器学习10-应用机器学习的建议

吴恩达机器学习10-应用机器学习的建议

1.改进算法的方法

1.尝试减少特征的数量
2.尝试获得更多的特征
3.尝试增加多项式特征
4.尝试减少正则化程度𝜆
5.尝试增加正则化程度𝜆

但是不应该随机选择上面的某种方法来改进我们的算法，而是运用一些机器学习诊断法来帮助我们知道上面哪些方法对我们的算法是有效的。

2.评估假设

当我们确定学习算法的参数的时候，我们考虑的是选择参量来使训练误差最小化，有人认为得到一个非常小的训练误差一定是一件好事，但我们已经知道，仅仅是因为这个假设具有很小的训练误差，并不能说明它就一定是一个好的假设函数。而且我们也学习了过拟合假设函数的例子（上图），所以这推广到新的训练集上是不适用的。

所以提出一种方法来评估我们的假设函数过拟合检验。

为了检验算法是否过拟合，我们将数据分成训练集和测试集，通常用 70%的数据作为训练集，用剩下 30%的数据作为测试集。很重要的一点是训练集和测试集均要含有各种类型的数据，通常我们要对数据进行“洗牌”，然后再分成训练集和测试集。

测试集评估在通过训练集让我们的模型学习得出其参数后，对测试集运用该模型，我

们有两种方式计算误差：

• 对于线性回归模型，我们利用测试集数据计算代价函数𝐽

  $J_{\text{test }}(\theta )=\frac{1}{2m_{\text{test }}}{\sum }_{i=1}^{M_{\text{test }}}{\left(h_{\theta }\left(x_{\text{test }}^{(i)}\right)-y_{\text{test }}^{(i)}\right)}^2$

• 对于逻辑回归模型，我们利用测试数据集来计算代价函数

  $J_{\text{test }}(\theta )=-\frac{1}{m_{\text{test }}}{\sum }_{i=1}^{m_{\text{tes }}}\log h_{\theta }\left(x_{\text{test }}^{(i)}\right)+\left(1-y_{\text{test }}^{(i)}\right)\log h_{\theta }\left(x_{\text{test }}^{(i)}\right)$

  还可以使用分类误差率：
  

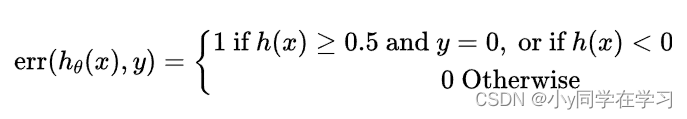
  然后对计算结果求平均

3.模型选择和交叉验证集

假设我们要在 10 个不同次数的二项式模型之间进行选择：

显然越高次数的多项式模型越能够适应我们的训练数据集，但是适应训练数据集并不代表着能推广至一般情况(过拟合，预测效果一般很差)，我们应该选择一个更能适应一般情况的模型。我们需要使用交叉验证集来帮助选择模型。

即：使用 60%的数据作为训练集，使用 20%的数据作为交叉验证集，使用 20%的数据作为测试集。

模型选择的方法为：

1. 使用训练集对上述多项式训练出 10 个模型

2. 用 10 个模型分别对交叉验证集计算得出交叉验证误差（代价函数的值）

3. 选取代价函数值最小的模型

4. 用步骤 3 中选出的模型对测试集计算得出推广误差（代价函数的值）

4.诊断偏差和方差

当你运行一个学习算法时，如果这个算法的表现不理想，那么多半是出现两种情况：要么是偏差比较大，要么是方差比较大。换句话说，出现的情况要么是欠拟合，要么是过拟合问题。那么这两种情况，哪个和偏差有关，哪个和方差有关?

我们通常会通过将训练集和交叉验证集的代价函数误差与多项式的次数绘制在同一张图表上来帮助分析：

Training error:

$J_{\text{train }}(\theta )=\frac{1}{2m}{\sum }_{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$

Cross Validation error:

$J_{cv}(\theta )=\frac{1}{2m_{cv}}{\sum }_{i=1}^m{\left(h_{\theta }\left(x_{cv}^{(i)}\right)-y_{cv}^{(i)}\right)}^2$

首先：

对于训练集，当 𝑑（多项式最高次数） 较小时，模型拟合程度更低，误差较大；随着 𝑑 的增长，拟合程度提高，误差减小。

对于交叉验证集，当 𝑑 （多项式最高次数）较小时，模型拟合程度低，误差较大；但是随着 𝑑 的增长，误差呈现先减小后增大的趋势，转折点是我们的模型开始过拟合训练数据集的时候。

其次：

训练集误差和交叉验证集误差近似时，左端红色：偏差/欠拟合
交叉验证集误差远大于训练集误差时，右端红色：方差/过拟合

5.正则化和偏差/方差

在训练模型的过程中，一般会使用一些正则化方法来防止过拟合。但是我们可能会正则化的程度太高或太小了，即我们在选择 λ 的值时也需要思考与刚才选择多项式模型次数类似的问题：

𝜆过大，欠拟合，导致高偏差

𝜆过小，过拟合，导致高方差

𝜆需要合适值

选择𝜆的方法为：
1.使用训练集训练出 12 个不同程度正则化的模型
2.用 12 个模型分别对交叉验证集计算的出交叉验证误差
3.选择得出交叉验证误差最小的模型
4.运用步骤 3 中选出模型对测试集计算得出推广误差，我们也可以同时将训练集和交叉验证集模型的代价函数误差与 λ 的值绘制在一张图表上：

• 当 𝜆 较小时，训练集误差较小（过拟合高方差）而交叉验证集误差较大
• 随着 𝜆 的增加，训练集误差不断增加（欠拟合高偏差），而交叉验证集误差则是先减小后增加

先通过训练集和交叉验证集训练好$\theta$，再训练好𝜆，选出最佳模型。

6.学习曲线

学习曲线就是一种很好的工具，我经常使用学习曲线来判断某一个学习算法是否处于偏差、方差问题。学习曲线是学习算法的一个很好的合理检验（sanity check）。学习曲线是将训练集误差和交叉验证集误差作为训练集实例数量（𝑚）的函数绘制的图表。

即，如果我们有 100 行数据，我们从 1 行数据开始，逐渐学习更多行的数据。思想是：当训练较少行数据的时候，训练的模型将能够非常完美地适应较少的训练数据，但是训练出来的模型却不能很好地适应交叉验证集数据或测试集数据。
$J_{\text{train }}(\theta )=\frac{1}{2m}{\sum }_{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$
$J_{cv}(\theta )=\frac{1}{2m_{cv}}{\sum }_{i=1}^{m_{cv}}{\left(h_{\theta }\left(x_{cv}^{(i)}\right)-y_{cv}^{(i)}\right)}^2$

高偏差情况：

在高偏差/欠拟合的情况下，训练集误差和交叉验证集误差一直很大，增加数据到训练集意义不大。

高方差情况：

在高方差/过拟合的情况下，训练集误差和交叉验证集误差一直存在差距，但是随着样本数的增加两者差距减少并且交叉训练集的误差开始降低，所以增加更多数据到训练集可能可以提高算法效果。

7.决定下一步做什么

• 诊断法则：

1. 获得更多的训练实例——解决高方差
2. 尝试减少特征的数量——解决高方差
3. 尝试获得更多的特征——解决高偏差
4. 尝试增加多项式特征——解决高偏差
5. 尝试减少正则化程度 λ——解决高偏差
6. 尝试增加正则化程度 λ——解决高方差

• 神经网络的方差和偏差：
  

使用较小的神经网络，类似于参数较少的情况，容易导致高偏差和欠拟合，但计算代价较小使用较大的神经网络，类似于参数较多的情况，容易导致高方差和过拟合，虽然计算代价比较大，但是可以通过正则化手段来调整而更加适应数据。

通常选择较大的神经网络并采用正则化处理会比采用较小的神经网络效果要好。

对于神经网络中的隐藏层的层数的选择，通常从一层开始逐渐增加层数，为了更好地作选择，和之前提到的思想一样，可以把数据分为训练集、交叉验证集和测试集，针对不同隐藏层层数的神经网络训练神经网络， 然后选择交叉验证集代价最小的神经网络。