二叉树相关题目

二叉树

 树一般都是利用递归去求解b

 

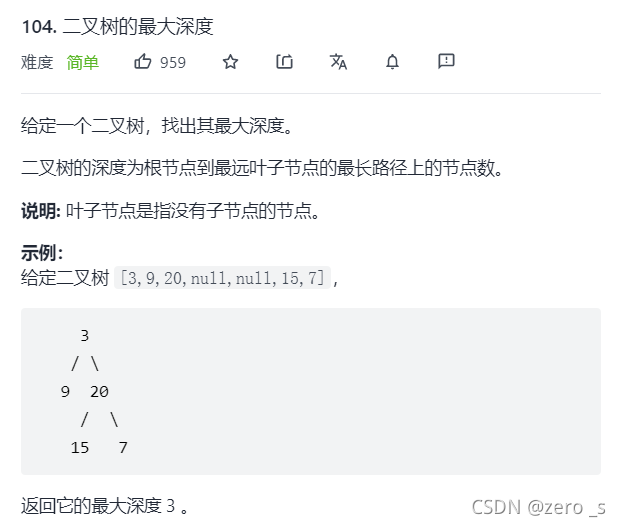
class Solution {
    public int maxDepth(TreeNode root) {

        // 利用dfs递归调用
      //  return root==null ?0 : Math.max(maxDepth(root.left),maxDepth(root.right))+1;


      // 方法2 广度优先遍历 bfs ，并利用队列按层去弹出和加入每层的叶子节点
      if(root == null){return 0;}

      Queue<TreeNode> queue = new LinkedList<>();  // 构建一个队列
      queue.offer(root);

      int res = 0;
      while(!queue.isEmpty()){ // 说明这一层有节点
          int size = queue.size();
          while(size>0){ // 内层循环是直接装下一层的节点，把下一层的所有都装进去
              TreeNode node = queue.poll();  // 需要弹出第一个节点来查询是否有下一层节点
              if(node.left != null){
                  queue.offer(node.left);
              }
              if(node.right != null){
                  queue.offer(node.right);
              }
              size--; // 每装一次，size需要减少一；
          }
          answer++;
      }
      return answer;

    }
}

 

class Solution {

    private boolean result = true;
    public boolean isBalanced(TreeNode root) {

        // 求树的高度，然后做差判断，树的高度利用dfs深度优先遍历

        MaxDepth(root);
        return result;
    }

    private int MaxDepth(TreeNode root){ //利用深度优先遍历求最大深度
        if(root ==null) return 0;

        // 找到当前节点为根节点的左右子树的高度
        int l = MaxDepth(root.left);
        int r = MaxDepth(root.right);

        // 判断左右子树的高度差
        if(Math.abs(l-r)>1){
            result = false;
        }
        // 递归需要去计算高度
        return 1+Math.max(l,r);
    }
}

 

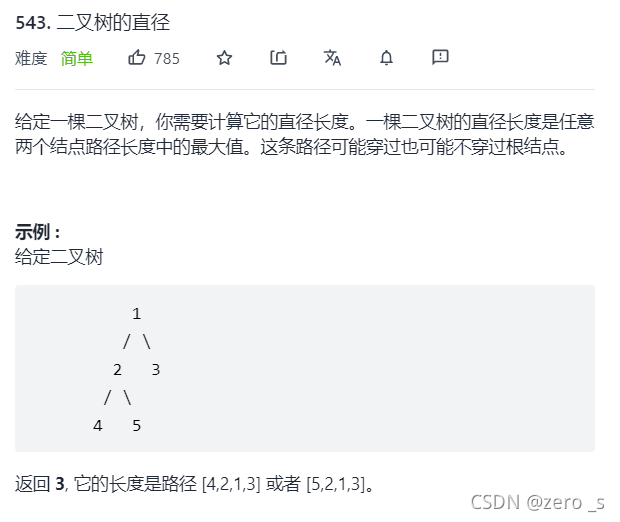
class Solution {
    private int max = 0;
    public int diameterOfBinaryTree(TreeNode root) {
        depth(root);
        return max;
    }

    private int depth(TreeNode root){
        if(root==null) return 0;

        int l =depth(root.left);
        int r =depth(root.right);
        // 需要和新的对比
        max = Math.max(max,l+r);

        // 返回递归的最大局部深度
        return 1+Math.max(l,r);
    }
}

 

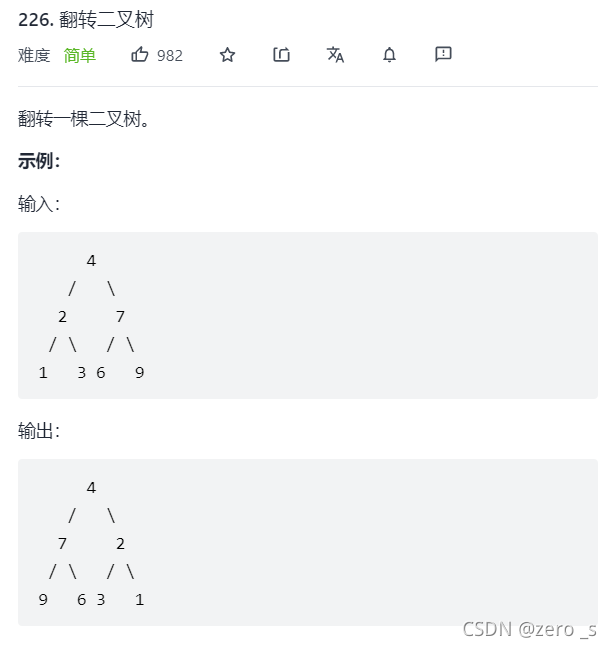
class Solution {
    public TreeNode invertTree(TreeNode root) {

        if(root == null) return null;

        // 让当前节点的左子树等于右子树，右子树等于左子树

        TreeNode temp = root.left;
        root.left =root.right;
        root.right = temp;
        invertTree(root.left);
        invertTree(root.right);
        return root;

    }
}

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1 == null && root2==null) return null;
        if(root1==null) return root2;
        if(root2==null) return root1;

        //如果对应相同位置的节点都有值就相加
        TreeNode root = new TreeNode(root1.val+root2.val);
        root.left = mergeTrees(root1.left,root2.left);
        root.right = mergeTrees(root1.right,root2.right);
        return root; 


    }
}

 

 

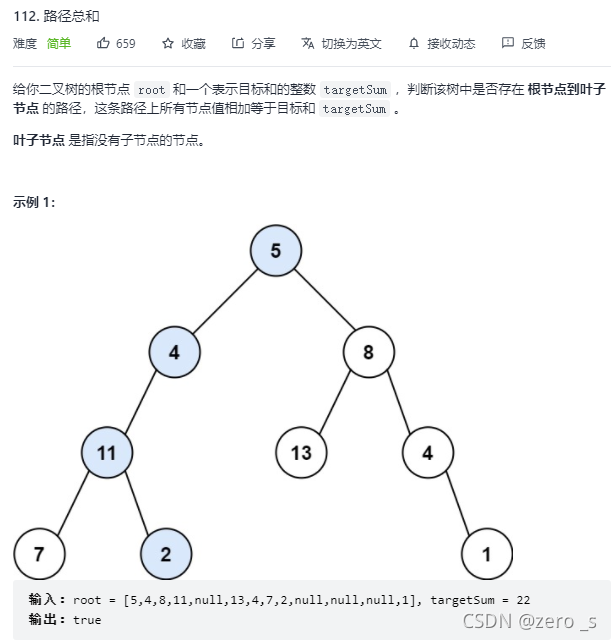
class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root==null) return false;
        
        if(root.left==null && root.right==null && root.val==targetSum) return true;

        // 递归并且原地自减
        return hasPathSum(root.left,targetSum-root.val) || hasPathSum(root.right,targetSum-root.val);

    }
}

 

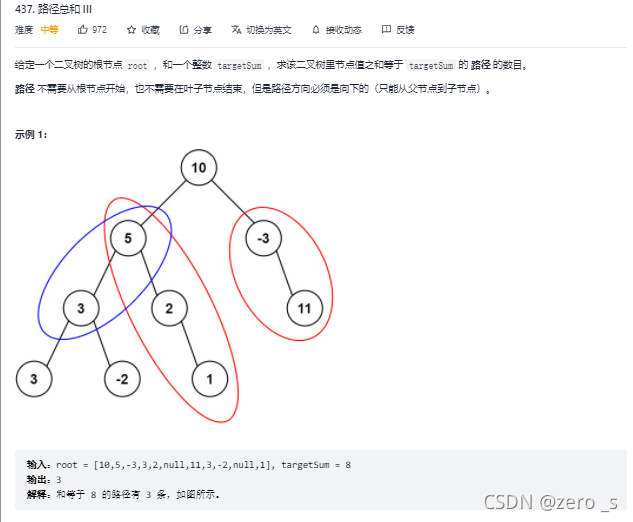
class Solution {
    public int pathSum(TreeNode root, int targetSum) {
        if(root==null) return 0;

        // 从根节点开始向下找，或者从其他非根节点开始往下找
        int result = pathSumWithRoot(root,targetSum)+pathSum(root.left,targetSum)+pathSum(root.right,targetSum);
        return result;
    }

     private int  pathSumWithRoot(TreeNode root,int targetSum){
         if(root==null) return 0;
         int result=0;
         if(root.val==targetSum) result++;
         result += pathSumWithRoot(root.left,targetSum-root.val) + pathSumWithRoot(root.right,targetSum-root.val);
         return result;
     }
}

 

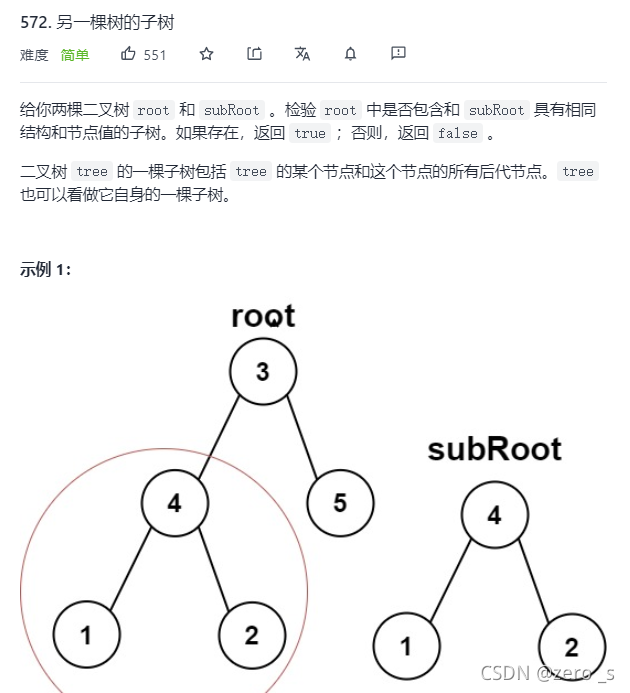
class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root ==null)return false;

        // r是自身的一颗子树或者递归根节点的左子树 或者递归根节点的右节点

        return isSubtreeWithRoot(root,subRoot) || isSubtree(root.left,subRoot) ||
         isSubtree(root.right,subRoot);

    }

    private boolean isSubtreeWithRoot(TreeNode root, TreeNode subRoot){
        if(root==null && subRoot ==null) return true; //

        if(root==null ||subRoot==null) return false;  // 匹配不同步

        if(root.val != subRoot.val ) return false; //匹配过程中任意一个节点的值不同

      // 继续向下传递
        return isSubtreeWithRoot(root.left,subRoot.left) && isSubtreeWithRoot(root.right,subRoot.right);

    }
}

 

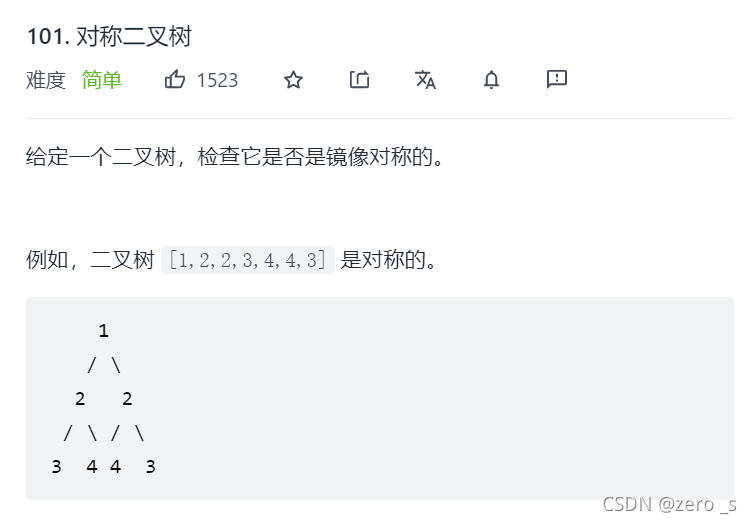
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root==null) return false;
        return isSymmetric1(root.left,root.right);
    }

    private boolean isSymmetric1(TreeNode t1,TreeNode t2){
        if(t1==null && t2 == null) return true;
        if(t1==null || t2== null) return false;
        if(t1.val != t2.val) return false;
        return isSymmetric1(t1.left,t2.right) && isSymmetric1(t1.right,t2.left);
    }
}

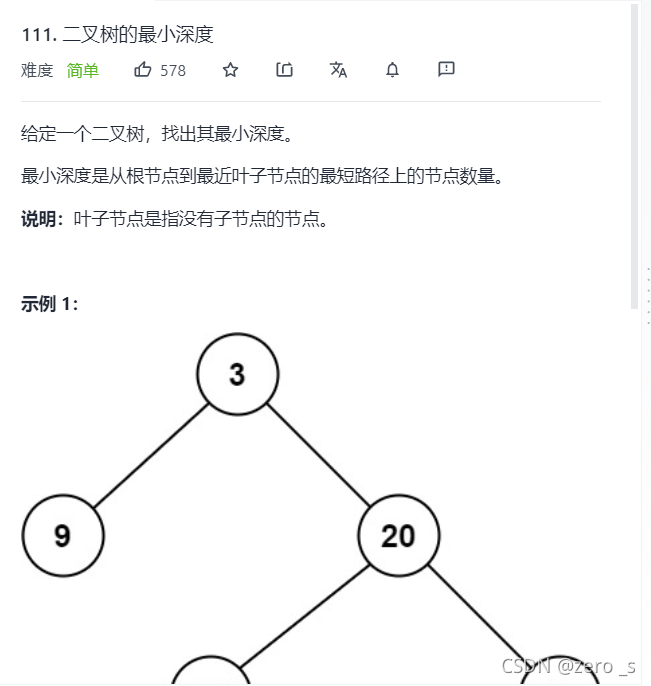
class Solution {
    public int minDepth(TreeNode root) {
        if(root==null) return 0;

        int left = minDepth( root.left);
        int right = minDepth(root.right);

        if(left==0 || right==0) return left+right+1;

        return  Math.min(left,right)+1;

    }
}

 

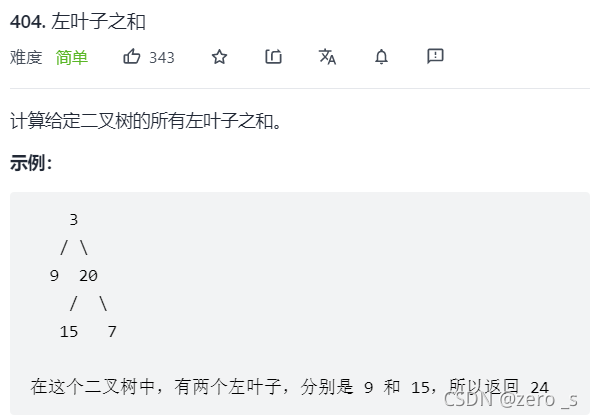
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if(root == null) return 0;
        if(isLeaf(root.left)) return root.left.val +sumOfLeftLeaves(root.right);
        return sumOfLeftLeaves(root.left) +sumOfLeftLeaves(root.right);

    }

    private boolean isLeaf(TreeNode node) {
        if(node == null) return false;
        return node.left==null && node.right==null;
    }
}

前序遍历： 根 左 右 

后续遍历： 左 右 根

中序遍历： 左 根 右