神经网络简介 & 利用minist数据集实现手写数字识别和识别精度计算

本博客借鉴了《深度学习入门：基于python的理论与实现》的第三章：神经网络

一.引子

博客主要介绍神经网络的前向传播。本章介绍的神经网络和上一章的感知 机在信号的按层传递这一点上是相同的，但是，向下一个神经元发送信号时， 改变信号的激活函数有很大差异。神经网络中使用的是平滑变化的sigmoid 函数，而感知机中使用的是信号急剧变化的阶跃函数。这个差异对于神经网 络的学习非常重要
。同时注意神经网络中激活函数必须非线性，否则多层网络无意义了。

二. 神经网络（三层简单实现）

2.1 总图

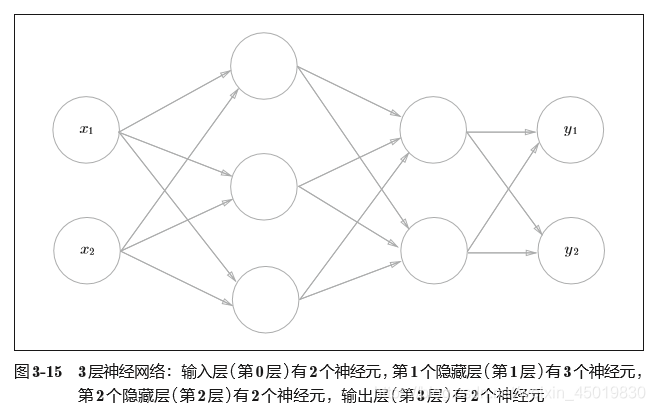
2.2输入层到第一层信号传递：

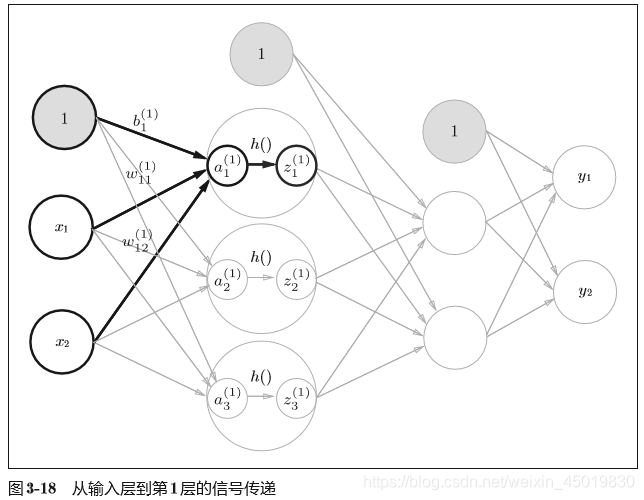
X = np.array([1.0, 0.5]) #输入
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]) #权重
B1 = np.array([0.1, 0.2, 0.3])#偏置 
print(W1.shape) # (2, 3) 
print(X.shape)  # (2,) 
print(B1.shape) # (3,)
A1 = np.dot(X, W1) + B1 #这个A1的结果还没有经过激活函数的运算
Z1 = sigmoid(A1) #激活后  上图中h()表示激活函数

2.3第一层到第二层的信号传递:

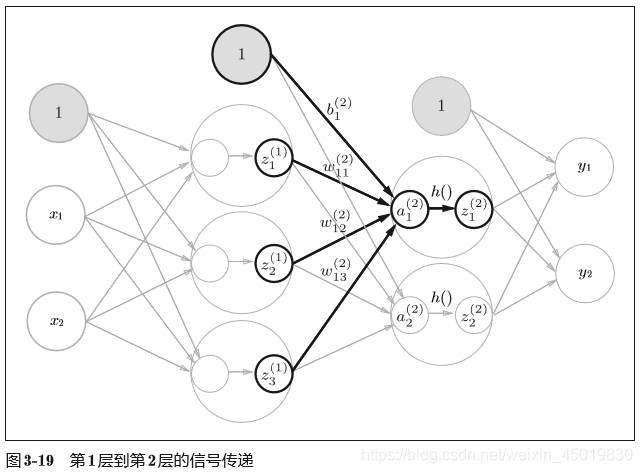
W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]) #权重
B2 = np.array([0.1, 0.2])#偏置
print(Z1.shape) # (3,) 
print(W2.shape) # (3, 2) 
print(B2.shape) # (2,)
A2 = np.dot(Z1, W2) + B2 #z1是当前的输入，是0~1层传递的输出
Z2 = sigmoid(A2)#激活后

2.4 第二层到输出的信号传递：

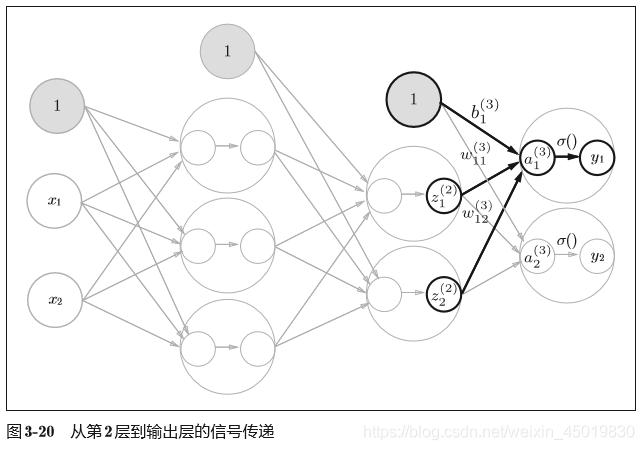
这里我们定义了identity_function()函数（也称为“恒等函数”），并将 其作为输出层的激活函数。恒等函数会将输入按原样输出，因此，这个例子 中没有必要特意定义identity_function()。这里这样实现只是为了和之前的 流程保持统一。另外，图3-20中，输出层的激活函数用σ()表示，不同于隐 藏层的激活函数h()（σ读作sigma）。另外，图3-20中，输出层的激活函数用σ()表示，不同于隐 藏层的激活函数h()

def identity_function(x):    
	return x
W3 = np.array([[0.1, 0.3], [0.2, 0.4]]) 
B3 = np.array(</