变分自编码VAE

前言

VAE模型是Kingma(也是Adam的作者)大神在2013年发表的文章，是一篇非常非常经典，且实现非常优雅的生成模型，同时它还为bayes概率图模型难以求解的问题提供了一种有效的思路。论文原名为Auto-Encoding Variational Bayes，是一种通用的利用auto-encoding方法结合variational lower bound求解bayes图模型隐变量的方法论。而VAE(Variational Auto-Encoding)是在该方法论下的一个具体示例。

先介绍一下有向图模型：

 有向图模型（Directed Graphical Model），也称为贝叶斯网络（Bayesian Network）或信念网络（Belief Network，BN），是一类用有向图来描述随机向量概率分布的模型。常见的有向图模型：很多经典的机器学习模型可以使用有向图模型来描述，比如朴素贝叶斯分类器、隐马尔可夫模型、深度信念网络等。

问题引入

下面正式开始变分自编码贝叶斯理论的内容：

在面对大量数据和具有难以处理的后验分布的连续潜在变量的情况下，如何有效的学习有向概率图模型的参数？

作者寻求AEVB(Auto-Encoding Variational Bayes)的通用求解算法，试图推断和学习有向概率图模型的隐分布  z，并通过对 z 的采样来实现数据生成。最后作者提出的方法为，使用标准的基于梯度的优化方法能够优化随机目标函数的所有参数。该方法不需要 Monte Carlo EM 方法对每个数据点进行昂贵的采样循环，并且与唤醒睡眠算法不同，它所有参数更新与边缘似然的变分下限的优化有关。

假设数据集为   ，是由连续或离散变量   x 采样得到的N个样本。假设数据是由随机过程产生，且包含一个不可见的连续随机隐变量  z，如右图所示。那样本生成的过程分为两步：1> 从先验分布 随机采样生成  ；2> 从条件概率分布     中采样生成   。但是这个过程在我们看来是隐藏的：真正的参数  以及潜在变量  的值对我们来说是未知的。

此处的公式以图片的格式展出，具体可以参考论文。

Search for Auto-Encoding Variational Bayes | Papers With Code

1312.6114v10.pdf (arxiv.org)

 文章对这三个问题提出了解决方案：

1. 参数 θ 的有效近似最大似然（ ML ）或最大后验（ MAP ）估计。它允许我们模拟隐藏的随机过程并生成类似于真实数据的人工数据。

2. 给定观察值 x 用于选择参数 θ 的潜在变量 z 的有效近似后验推断。这对于编码或数据表示任务很有用。

3. 变量 x 的有效近似边缘估计。这使我们能够执行需要先验 x 的各种推理任务。计算机视觉中的常见应用包括图像去噪、修复和超分辨率。

 

 

作者并未对    进行建模 。作者使用     作为编码器，它会产生z的可能值分布（例如高斯分布）。由每一个样本点x，可以学出一个对应的隐层分布z（注意，此处为每一个样本均可学出其对应的隐层z分布）；并使用     作为（生成）解码器，实现模型生成。下面的公式帮助大家更形象的理解这个过程。

 变分界

 那么上述构建的模型   和   中的参数  和  该如何训练呢？

 基于生成式模型，我们需要最大化边缘似然概率，边缘似然由单个数据点的边缘似然之和组成

 其中i代表样本，每个数据点可以被写成

 根据KL散度性质，有  。因此     为第i个样本边缘似然的下界：

重参数化变分下界

重参数化变分下界——获取变分下界的关于  的可微估计 ：

对于后验估计    ，重新参数化它的条件采样       为        

 使得先验函数     和函数    让下式成立：

 简化三个PDFs（概率密度函数）为

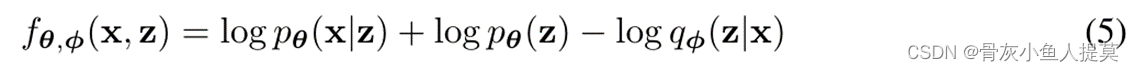
 给定数据点    ，变分下限的蒙特卡罗估计为

此时估计器仅仅从  中进行采样并且不受参数 的影响，因此可以将公式（6）作为目标函数，它是可微的，并且能对参数   和  同时进行优化。 

 从𝒩  中进行采样Z，相当于从𝒩 中采样一个  并且令，

 

运用

假设隐藏层变量z的先验分布为各向同性高斯分布   。令 （解码器）是一个多元伯努利，其概率是从 z 计算得出的，解码器是具有单个隐藏层的全连接神经网络

 

虽然选择 qφ(z|x)（解码器）有很大的自由度，但我们暂时假设一个相对简单的情况：假设真正的后验 pθ(z|x) 呈现近似高斯形式具有近似对角的协方差。在这种情况下，我们可以让变分近似后验为具有对角协方差结构的多元高斯：

 

 

 最后的目标函数

参考资料：

1312.6114v10.pdf (arxiv.org)

Search for Auto-Encoding Variational Bayes | Papers With Code