插入排序及归并排序（附C++代码）

插入排序及归并排序（附C++代码）

该算法对于少量元素的排序是一个有效的算法。
伪代码（写代码时可以参照）：

INSERTION-SORT（A）
for  j=1 to A.length
	key=A[j]
	i=j-1
	while i>=0 and A[i]>key
		A[i+1]=A[i]
		i++
	A[i+1]=key

对插入排序算法的分析：

假定:
第i行的每次执行时间ci
tj表示对j第4行执行while循环测试的次数
n=A.length
$m_1$=$\sum _{j=2}^n{t}_j$
$m_2$=$\sum _{j=2}^n(t_j-1)$

INSERTION-SORT（A）                                  代价                           次数
for  j=1 to A.length	                             c1                             n
	key=A[j]                                     c2				    n-1
 	i=j-1                                        c3                             n-1
 	while i>=0 and A[i]>key                      c4                             m1
 		 A[i+1]=A[i]                         c5                             m2
  		 i++                                 c6                             m2
	 A[i+1]=key				     c7                             n-1

运行时间

$T_n$=$c_1$n+$c_2$(n-1)+$c_3$(n-1)+$c_4$$\sum _{j=2}^n{t}_j$+$c_5$$\sum _{j=2}^n(t_j-1)$+$c_6$$\sum _{j=2}^n(t_j-1)$+$c_7$(n-1)
若输入的数是已排好的数，为最佳情况，此时$t_j$ =1
$T_n$=$c_1$n+$c_2$(n-1)+$c_3$(n-1)+$c_4$(n-1)+$c_7$(n-1)
=($c_1$+$c_2$+$c_3$+$c_4$+$c_7$)n-($c_2$+$c_3$+$c_4$+$c_7$)
可以看为 an+b
若输入数组为反向排序，为最坏情况，此时$t_j$ =j
$T_n$=$c_1$n+$c_2$(n-1)+$c_3$(n-1)+$c_4$(n(n-1)/2-1)+$c_5$n(n-1)/2+$c_6$n(n-1)/2+$c_7$(n-1)
=($c_4$/2+$c_5$/2+$c_6$/2)$n^2$+($c_1$+$c_2$+$c_3$-$c_4$/2-$c_5$/2-$c_6$/2+$c_7$)n-($c_2$+$c_3$+$c_4$+$c_7$)
可以看为 a$n^2$+bn+c

我们集中于最坏情况运行时间，因为最坏运行时间为运行时间的一个上界，在某些算法里最坏情况经常出现，“平均情况”往往与最坏情况大致一样。
对于a$n^2$+bn+c，当n很大时，我们忽略低阶项和最重要项常系数，故可化为$n^2$

设计算法

分治法

伪代码

MERGE<A,p,q,r>
n1=q-p+1
n2=r-q      
for i=1 to n1
	L[i]=A[p+i-1]
for j=1 to n2
	R[j]=A[q+j]            //将数组分为L[1...n1+1]和R[1...n2+1]两个数组,假设这两个数组都是已排好序的
L[n1+1]=
R[n2+1]=                       //设置哨兵牌，来知道是否有数组到末尾，如果到了直接将另一组数全部放到新数组中
i=1
j=1
for k=p to r
	if L[i]<=R[j]
		A[k]=L[i]
		i++
	else A[k]=R[j]
		j++	

运行时间为n, n=r-p+1.
上面那段伪代码是假设分成了已经排好序的两段代码，而事实大多数不会如此。
所以现在把MERGE作为归并排序的子程序使用，将A[p…r]分成两个子数组A[p…q]和A[q+1…r],前者包含大于等于n/2最小整数个元素，后者包含小于等于n/2最大整数个元素，这样一直分下去直到分为含有小于等于两个元素的数组。当为两个元素时再用MEGER函数将两个元素排好序作为再次使用MEGER的两个排好序的数组中的一个再次进行MEGER，如此继续重复上面步骤知道将原数组分成两个已排好序的数组，最后再用这两个数组进行MEGER得到排好序的原数组。

下面举个例子

对于A=[3,41,52,26,38,57,9,49]

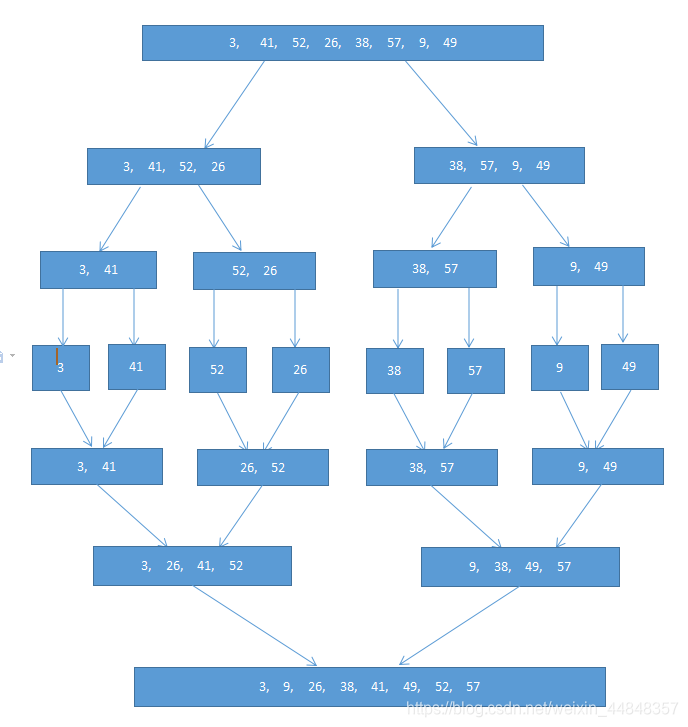
这是对数组分为两组后得到未排序的两组数组进行排序的伪代码：

MERGE-SORT(A,p,r)
if p<r
	q=[(p+r)/2]               //小于等于（p+r）/2 的最大整数
	MERGE-SORT(A,p,q)
	MERGE-SORT(A,q+1,r)
	MERGE(A,p,q,r)

插入排序法代码（C++）

#include<iostream>
using namespace std
int main(){
int A[8]={3,41,52,26,38,57,9,49};
for(int j=1;j<8;j++){
	int key=A[j];
	int i=j-1;
	while((i>=0)&&(A[i]>key)){
		A[i+1]=A[i];
		i--;
		}
	A[i+1]=key;
	}
for(int i=0;i<8;i++){
	cout<<A[i]<<" ";	
	}
	cout<<endl;
	system("pause");
}

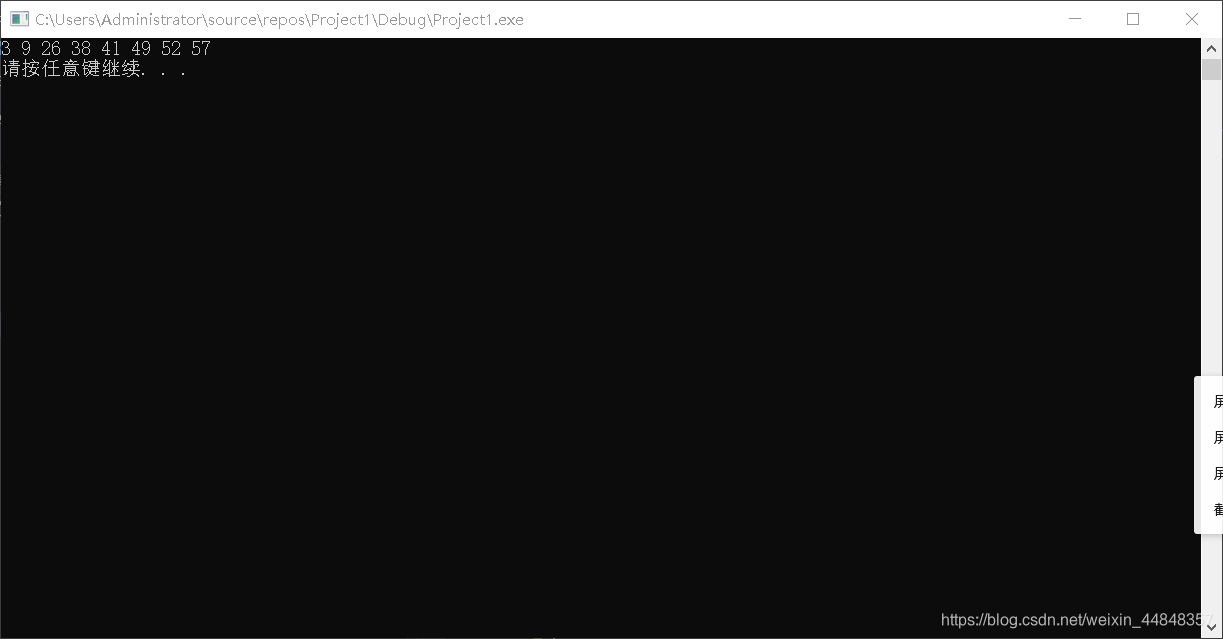
归并排序法代码（C++）

#include<iostream>
using namespace std;
void MERGE(int A[],int p,int q,int r);
void MERGESORT(int A[],int p,int r);
int main(){
	int A[8]={3,41,52,26,38,57,9,49};
	MERGESORT(A,0,8);
	for(int i=0;i<8;i++){
		cout<<A[i]<<" ";
	}
	cout<<endl;
	system("pause");
}
void MERGE(int A[],int p,int q,int r){
	int mid=q;
	int left=p;
	int B[8];       //这里B作为临时数组，建议用指针。
	for(int k=p;k<r;k++){
		if((p<mid)&&(q<r)){                    //对两组数进行比较较小的放入暂时数组
			if(A[p]<=A[q]){
				B[k]=A[p];
				p++;
			}
			else{
				B[k]=A[q];
				q++;
			}
		}
		else{                               //下面是检测是否有一组数到了末尾
			if((p<mid)&&(q>=r)){
				B[k]=A[p];
				p++;
			}
			if((p>=mid)&&(q<r)){
				B[k]=A[q];
				q++;
			}
		}
	}
	p=left;
	for(int i=0;i<r;i++){
		A[i]=B[i];
	}
}
void MERGESORT(int A[],int p,int r){
	if(p<(r-1)){
		int q=(p+r)/2;
		MERGESORT(A,p,q);
		MERGESORT(A,q,r);
		MERGE(A,p,q,r);
	}	
}

结果同上