吴恩达机器学习4--正则化(Regularization)

过拟合问题

看下面回归的例子

第一个模型是一个线性模型，欠拟合，不能很好地适应我们的训练集；第三个模型是一个四次方的模型，过于强调拟合原始数据，而丢失了算法的本质。而中间的模型似乎最合适
在分类问题中：

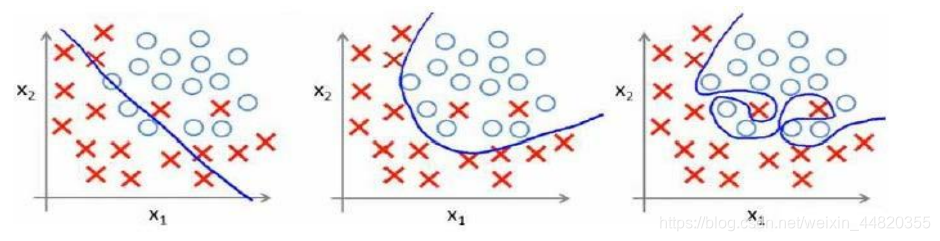
就以多项式理解，𝑥 的次数越高，拟合的越好，但相应的预测的能力就可能变差

正则化线性回归

正则化线性回归的代价函数为：

正则化线性回归的梯度下降算法为：

可以看出，正则化线性回归的梯度下降算法的变化在于，每次都在原有算法更新规则的基础上令𝜃值减少了一个额外的值。
同样我们也可以用正规方程来解正则化线性回归模型

图中的矩阵尺寸为 (𝑛 + 1) ∗ (𝑛 + 1)

正则化逻辑回归

代价函数：

import numpy as np
def costReg(theta, X, y, learningRate):
	theta = np.matrix(theta)
 	X = np.matrix(X)
 	y = np.matrix(y)
 	first = np.multiply(-y, np.log(sigmoid(X*theta.T)))
 	second = np.multiply((1 - y), np.log(1 - sigmoid(X*theta.T)))
 	reg = (learningRate / (2 * len(X))* np.sum(np.power(theta[:,1:theta.shape[1]],2))
 return np.sum(first - second) / (len(X)) + reg

梯度下降算法为