「AAAI2021」【Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecast】论文笔记

Paper：https://arxiv.org/abs/2012.07436v2
Code：https://github.com/zhouhaoyi/Informer2020

Abstract

这篇工作的主要内容是通过高效的Transformer模型对长序列时序数据进行预测，即：LSTF(Long sequence time-series forecasting)。 区别于短序列的时序数据，LSTF需要模型具有较高的预测能力，从而高效的捕获输入和输出之间精确的相关耦合关系。

原文： Long sequence time-series forecasting (LSTF) demands a high prediction capacity of the model, which is the ability to capture precise long-range dependency coupling between output and input efficiently.

近期Transformer模型的就表现出了较高的模型预测能力。然而，当前的Transformer模型存在一些问题，从而阻碍了其直接应用于LSTF。这些问题包括：

• 二次时间复杂度（quadratic time complexity）
• 高内存使用率（high memory usage）
• 编码器-解码器体系结构的固有局限性（inherent limitation of the encoder-decoder architecture）

为了解决以上问题，本文设计了一个高效的基于Transformer的模型，用于LSTF，并命名为Informer。Informer模型有如下三个特点：

1. ProbSparse自注意力机制(ProbSparse Self-attention mechanism)：可以达到$O(LlogL)$的时间复杂度和内存使用率，并可以取得与原模型相当的相关性对齐性能(has comparable performance on sequences’ dependency alignment)。
2. 自注意力蒸馏(self-attention distilling)通过将cascading层的输入减半来突出注意力集中，并且高效的处理过长的输入序列。

原文：(ii) the self-attention distilling highlights dominating attention by halving cascading layer input, and efficiently handles extreme long input sequences.

• [Q: What is cascading layer?]
• [Q: What is dominating attention?]

3. 生成式的decoder，虽然在概念上简单，但是通过一次向前操作而不是step-by-step的方式来预测长序列可以极大的提高长序列的inference速度。

原文：(iii) the generative style decoder, while conceptually simple, predicts the long time-series sequences at one forward operation rather than a step-by-step way, which drastically improves the inference speed of long-sequence predictions.

最后通过在四个大数据集上的广泛实验，验证了Informer的效果。

1. Introduction

时间序列的预测是许多领域（诸如经济金融、疾病传播分析等）的重要组成部分。然而，随着序列的长度逐渐变长，现有的模型遇到了极大的挑战。例如，Fig.1显示了使用LSTM模型预测一个变电站的每小时温度数据，随着预测序列长度逐渐增大，均方误差MSE明显提高，预测的速度也迅速变慢。

因此，对于长序列时序数据的预测，即：LSTF(Long sequence time-series forecasting)。其主要挑战是增强模型的预测能力以满足不断增加的序列长度。这一挑战需要满足如下两方面能力：

1. 强大的长范围的对齐能力（extraordinary long-range alignment ability）；
2. 长序列输入输出的高效运算（efficient operations on long sequence in- puts and outputs）.

近期，Transformer模型在捕获长范围依赖性方面相较于RNN模型，表现出了更好的性能。自注意力机制可以将模型中信号传播的路径的最大长度减小至理论上最短的$\mathcal{O}(1)$，并且避免了循环的结果（ recurrent structure）。因此，可将Transformer模型用于LSTF问题。
然而，Transformer模型中的自注意力机制对于长度为$L$的输入输出需要$L$-平方（$L$-quadratic）的计算和内存消耗，这违反了上面提到的第二个能力。因此，Transformer模型中自注意力机制的高效性成为了将其运用在LSTF问题上的瓶颈。总的来说，将原始的Transformer模型用于LSTF问题有如下三个限制：

1. 自注意力的二次计算复杂度$\mathcal{O}(L^2)$（The quadratic computation of self-attention）。二次复杂度主要来源于自注意力记住中的原子操作（atom operation），也称为规范点积（canonical dot-product）;
2. 对于长序列输入的层堆叠导致的内存瓶颈（The memory bottleneck in stacking layers for long
   inputs）。 每堆叠$J$个encoder/decoder层，就会使得内存使用率变为$\mathcal{O}(J\cdot L^2)$，从而使得难以使用长序列输入；
3. 预测长输出的速度下降（The speed plunge in predicting long outputs）。 原始Transformer的动态decoding使得step-by-step预测变得和RNN-based模型一样慢。

一些解决自注意力高效性的工作：

但以上工作均关注了limitation 1，但是2和3没有被解决。本文贡献如下：

• 提出Informer来增强对于LSTF问题的预测能力，Informer基于Transformer-based模型的潜在值（potential value）捕获长序列时间序列输出和输入之间的各个长范围（long-range）相关性；
• 提出ProbSparse自注意力机制来高效的替代传统的自注意力机制，并且达到了$\mathcal{O}(L\log L)$的时间复杂度和内存使用率；
• 提出了自注意力蒸馏操作特权来主导第$J$个堆叠层的自注意力分数，并将整体的复杂度降为$\mathcal{O}((2-ϵ)L\log L)$;
• 提出生成式的Decoder来获取长序列的输出，且只需要一步的前向传播；同时避免在推理阶段累积误差的扩散。

2. Preliminary

对于给定窗口size的rolling forecasting setting（应该就是把一个长的输入序列切成多个相同长度的短序列），设$t$时刻输入为 X t = { x 1 t , ⋯   , x L x t ∣ x i t ∈ R d x } \mathcal{X}^t=\{x^t_1,\cdots,x^t_{L_x}|x^t_i\in \mathbb{R}^{d_x}\} Xt={x1t​,⋯,xLx​t​∣xit​∈Rdx​}，对应的输出序列为 Y t = { y 1 t , ⋯   , y L y t ∣ y i t ∈ R d y } \mathcal{Y}^t=\{y^t_1,\cdots,y_{L_y}^t|y^t_i\in\mathbb{R}^{d_y}\} Yt={y1t​,⋯,yLy​t​∣yit​∈Rdy​}。其中LSTF问题意味着输出序列长度$L_y$更长，且输出维度$d_y\ge 1$。

Encoder-decoder结构

多数流行的模型将输入${\mathcal{X}}^t$编码为一种隐藏状态的表示 H t = { h 1 t , ⋯   , h L h t } \mathcal{H}^t=\{h^t_1,\cdots,h^t_{L_h}\} Ht={h1t​,⋯,hLh​t​}，并在输出进行解码以得到${\mathcal{Y}}^t$。Inference是通过step-by-step的过程，基于前一个隐藏状态的$h_k^t$来解码计算出新的隐藏状态$h_{k+1}^t$以及第$k$步其余的必要输出，之后在预测出第$k+1$步的输出序列$y_{k+1}^t$。这一过程也称为dynamic decoding。

输入表示「Appendix B」

对于RNN模型的输入：获取时间序列模式的方法是循环结构本身，也就是仅仅依赖time stamps；
对于原始的Transformer模型使用点对点的自注意力机制（point- wise self-attention mechanism），time stamps作为局部位置的上下文。
但是，对于LSTF问题，获取long-range的独立性需要全局的信息，例如：层次结构time stamp（周、月、年）和不可知论（agnostic）time stamps（如：假期、事件）。这些time stamps难以用于传统的自注意力，因此在encoder和decoder之间造成了query-key的不匹配，从而导致预测性能下降。 为了缓解这一问题，本文给出了统一的输入表示，如Fig.6。

设，第$t_{th}$输入序列为${\mathcal{X}}^t$以及$p$种全局time stamps，且经过输入表示的特征维度为$d_{model}$。首先通过固定的position embedding来保留局部上下文，即：$P{E}_{(pos,2j)}=\sin (pos/(2L_x{)}^{2j/d_{model}})$，$P{E}_{(pos,2j+1)}=\cos (pos/(2L_x{)}^{2j/d_{model}})$，其中 j ∈ { 1 , ⋯   , ⌊ d m o d e l / 2 ⌋ } j\in{\{1,\cdots,\lfloor d_{model}/2\rfloor}\} j∈{1,⋯,⌊dmodel​/2⌋}。
此外，任一全局time stamp由一个限制词长的可学习的stamp embeddings $S{E}_{pos}$使用。也就是说自注意力的相似度计算可以访问全局上下文，并且可以承担长输入的计算消耗。
为了对齐维度，我们使用1-D的卷积（$k=3,s=1$）将标量文本$x_i^t$映射为$d_{model}$维向量$u_i^t$，因此输入向量（feeding vector）为：

$${\mathcal{X}}_{feed[i]}^t=\alpha u_i^t+P{E}_{(L_x\times (t-1)+i,)}+\sum _p[S{E}_{(L_x\times (t-1)+i,)}{]}_p$$

其中， i ∈ { 1 , ⋯   , L x } i\in{\{1,\cdots,L_x\}} i∈{1,⋯,Lx​}，$\alpha$是平衡全局\局部embedding和标量映射大小的因子。若输入序列被标准化，$\alpha =1$。

3. Methodology

当前时间序列预测可以粗略分为传统时序方法以及深度学习方法（主要基于RNN及其变体的encoder-decoder预测形式）。本文提出的Informer保留了encoder-decoder的结构，同时目标是解决LSTF问题。Fig.2为总体结构。

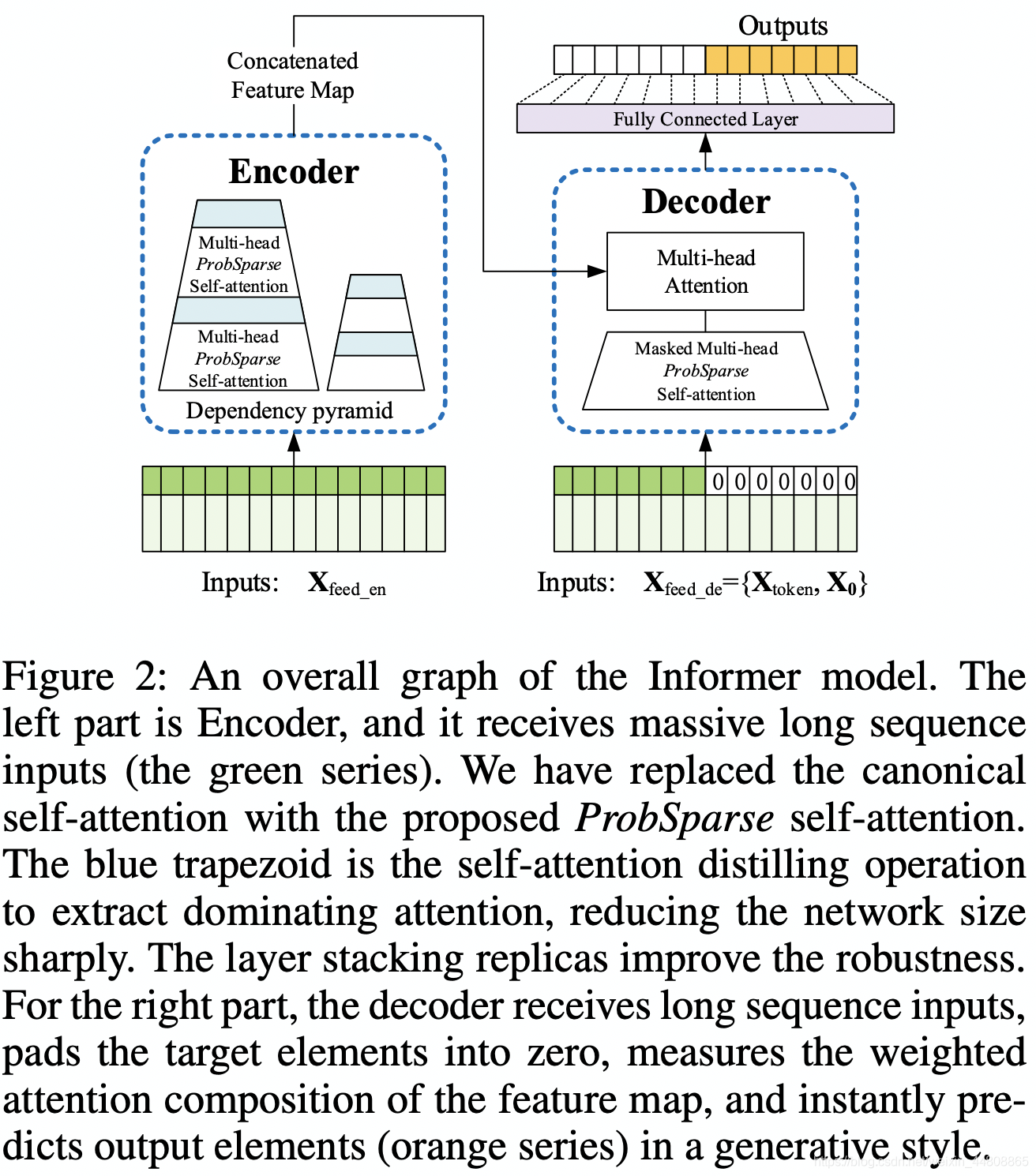
Efficient Self-attention Mechanism

【先给一个链接是从common的视角介绍Transformer中一些比较重要的问题的，包括attention，self-attention等，个人感觉写的不错，也可以帮助更好的理解这篇文章后面的内容：https://mp.weixin.qq.com/s/OSTJx-JSpoeMVEKZRjVZXA】

对于传统的self-attention，输入为元祖$(query,key,value)$，并且通过点乘的形式得到输出$\mathcal{A}(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d}})V$，其中$Q\in {\mathbb{R}}^{L_Q\times d},K\in {\mathbb{R}}^{L_K\times d},V\in {\mathbb{R}}^{L_V\times d},d$是输入维度。设$q_i,k_i,v_i$为$Q,K,V$的第$i$行，则由（Tsai et al. 2019）[1]，第$i$个query的attention被定义为概率形式的核平滑（kernel smoother in a probability form）：

$$\mathcal{A}(q_i,K,V)=\sum _j\frac{k(q_i,k_j)}{k({\sum }_{l}k(q_i,k_l))}{v}_j={\mathbb{E}}_{p(k_j|q_j)}[v_j](1)$$

其中，$p(k_j|q_i)=\frac{k(q_i,k_j)}{{\sum }_{l}k(q_j,k_l)},k(q_i,k_j)$为非对称的指数核$\exp (\frac{q_j{k}_j^T}{\sqrt{d}})$（p.s.这里就是把Softmax写出来了）。

self-attetion通过计算概率$p(k_j|q_i)$来得到输出。这样的运算需要二次复杂的的点乘运算以及$\mathcal{O}(L_Q{L}_K)$的内存使用率，这影响了预测能力。

一些之前的工作发现self-attention概率的分布存在潜在的稀疏性，因此设计了一些选择$p(k_j|q_i)$的策略并保证没有明显的性能下降。包括Sparse Transformer (Child et al. 2019)[2]、LogSparse Transformer (Li et al. 2019)[3]、 Longformer (Beltagy, Peters, and Cohan 2020) [4]。但以上方法均通过启发式的方法来进行理论分析，并且对于所有self-attention的head均采用相同的稀疏策略，阻碍了进一步的改进。

为了解决以上问题，我们首先对传统self-attention中学习attention的模型进行了定性的评估。self-attention的score的稀疏性服从长尾分布，即：只有很少的点乘组合对于主要的attention有贡献，其他的可以忽略。因此主要的问题是如何区分。

Query Sparsity Measurement

根据公式(1)将概率$p(k_j|q_i)$称为第$i$个query对所有keys上的attention，且输出为$p(k_j|q_i)$和value的组合。主要的点积对使得attention$p(k_j|q_i)$的分布远离均匀分布。若$p(k_j|q_i)$近似服从均匀分布，即$p(k_j|q_i)=\frac{1}{L_K}$，则self-attention变为微不足道的values的和，这个和对于输入是冗余的。一般来说，分布$p$和$q$的相似性可以区分queries的重要性。我们通过KL散度来衡量相似性，并丢弃掉常数项：

$$M(q_i,K)=\ln \sum _j^{L_K}{e}^{\frac{q_i{k}_j^T}{\sqrt{d}}}-\frac{1}{L_K}\sum _{j=1}^{L_K}\frac{q_i{k}_j^T}{\sqrt{d}}(2)$$

其中，第一项为$q_i$在所有keys上的对数指数和(Log-Sum-Exp, LSE)，第二项是他们的算术平均。若第$i$个query有更大的$M(q_i,K)$则它的attention概率$p$更加不同，并且在self-attention的长尾分布的头部部分拥有更大的可能包含主要的点积组合对。

ProbSparse Self-attention

基于以上度量方法，我们提出了ProbSparse Self-attention，从方法只允许每一个key注意$u$个主要的queries：
$$\mathcal{A}(Q,K,V)=softmax(\frac{\overline{Q}{K}^T}{\sqrt{d}})V(3)$$

其中，$\overline{Q}$为一个系数矩阵，其size等于q，且在稀疏度量$M(q,K)$下，只包含Top-$u$个queries。在一个采样因子常数$c$的控制下，设$u=c\cdot \ln L_Q$，这使得ProbSparse Self-attention只对于每一个query-key的lookup需要计算$\mathcal{O}(\ln L_Q)$的点乘运算，并且内存使用率仍为$\mathcal{O}(L_K\ln L_Q)$。

然而，在计算queries的度量$M(q,K)$是，穷计算复杂度仍是二次的$\mathcal{O}(L_Q{L}_K)$，并且LSE运算存在潜在的数值稳定性问题。为了解决这一问题，作者提出了对于query稀疏度量的近似方法：

$\text{Lemma 1.}$ 对于任意query $q_i\in {\mathbb{R}}^d$以及keys集合K中的$k_j\in {\mathbb{R}}^d$，有 ln ⁡ L K ≤ M ( q i , K ) ≤ max ⁡ j { q i k j T d } − 1 L K ∑ j = 1 L K { q i k j T d } + ln ⁡ L K \ln{L_K}\le M(q_i,K)\le \max_j{\{\frac{q_ik_j^T}{\sqrt{d}}\}}-\frac{1}{L_K}\sum_{j=1}^{L_K}{\{\frac{q_ik_j^T}{\sqrt{d}}\}}+\ln{L_K} lnLK​≤M(qi​,K)≤maxj​{d ​qi​kjT​​}−LK​1​∑j=1LK​​{d ​qi​kjT​​}+lnLK​。当$q_i\in K$，上式仍成立。

Lemma 1.的证明感兴趣的可以看原文Appendix D.1。基于上面的引理，作者提出了最大均值度量(max-mean measurement)：
M ‾ ( q i , K ) = max ⁡ j { q i k j T d } − 1 L K ∑ j = 1 L K q i k j T d ( 4 ) \overline{M}(q_i,K)=\max_j{\{\frac{q_ik_j^T}{\sqrt{d}}\}}-\frac{1}{L_K}\sum_{j=1}^{L_K}\frac{q_ik_j^T}{\sqrt{d}}\quad (4) M(qi​,K)=jmax​{d ​qi​kjT​​}−LK​1​j=1∑LK​​d ​qi​kjT​​(4)

$\text{Proposition 1.}$设$k_j\sim \mathcal{N}(\mu ,\Sigma )$，且令$q{k}_i$表示集合 { ( q i k j T ) / d ∣ j = 1 , ⋯   , L K } \{(q_ik_j^T)/\sqrt{d}|j=1,\cdots,L_K\} {(qi​kjT​)/d ​∣j=1,⋯,LK​}，则$\forall M_m={\max }_{i}M(q_i,K)$存在$\kappa >0$，使得 ∀ q 1 , q 2 ∈ { q ∣ M ( q , K ∈ [ M m , M m − κ ] ) } \forall q_1,q_2\in{\{q|M(q,K\in{[M_m,M_{m-\kappa}]})\}} ∀q1​,q2​∈{q∣M(q,K∈[Mm​,Mm−κ​])}，若$\overline{M}(q_1,K)>\overline{M}(q_2,K)$且$Var(q{k}_1)>Var(q{k}_2)$，则有很高的概率认为$M(q_1,K)>M(q_2,K)$。（证明见Appendix D.2）

Top-$u$的顺序对于命题1中的边界松弛成立。在长尾分布下，作者随机取$U=L_Q\ln L_K$个点积对来计算$\overline{M}(q_i,K)$，并将其他点积对设为0。而后选Top-$u$个作为$\overline{Q}$。实际中$L_K=L_Q=L$，因此ProbSparse Self-attention的计算和空间复杂度为$\mathcal{O}(L\ln L)$。

Encoder: Allowing for processing longer sequential inputs under the memory usage limitation

encoder部分主要用来获取长序列输入的鲁棒long-range相关性。设经过输入表示后，$t_{th}$序列${\mathcal{X}}^t$被reshape为矩阵${\text{X}}_{fee{d}_{en}}^t\in {\mathbb{R}}^{L_x\times d_{model}}$。Fig.3为encoder的示意图。

P.S.个人感觉上面这个图实在是画的不清楚。。。太乱了

Self-attention Distilling

由于经过ProbSparse Self-attention，encoder的输出feature map具有value $V$的冗余组合。因此作者使用了一个distilling的操作去减少输入的time维度。对于从$j$-$th$层到$(j+1)$-$th$的蒸馏具体操作如下：
$${\text{X}}_{j+1}^t=MaxPool(ELU(Conv1d([{\text{X}}_j^t{]}_{AB})))(5)$$

其中$[\cdot {]}_{AB}$包括Multi-head的ProbSparse Self-attention以及attention block中的其他基础的运算。以上操作直接将整个的空间复杂度等比例的减小为$\mathcal{O}((2-ϵ)L\ln L)$。而后为了增强蒸馏操作的鲁棒性，作者做了一些副本，并在最后concatenate起来得到最终的hidden representation of encoder。

Decoder: Generating long sequential outputs through one forward procedure

作者使用了两个head的相同Masked attention层作为decoder的结构，但是使用了生成式的inference方法来加速长序列的预测速度。特别的，输入decoder的向量为：
$${\text{X}}_{fee{d}_{de}}^t=Concat({\text{X}}_{token}^t,{\text{X}}_0^t)\in {\mathbb{R}}^{(L_{token}+L_y)\times d_{model}}$$
具体形式Fig.2有画出，${\text{X}}_0^t$是一个占位符，初值为0。最后再后面加了一层fc层得到最终的维度为$d_y$的输出。

Generative Inference

式（5）的形式主要源于NLP中的dynamic decoding（NLP中S作为start token，E作为结束字符）。作者将早于输出序列的$L_{token}$这么长的序列作为输入（例如预测7天的温度，那么用已知的5天温度作为start token，即 X f e e d d e = { X 5 d , X 0 } \textbf{X}_{feed_{de}}=\{\textbf{X}_{5d},\textbf{X}_0\} Xfeedde​​={X5d​,X0​}）。

Loss function

MSE loss

4. Experiment

Datesets

• ETT( (Electricity Transformer Temperature))
• ECL(Electricity Consuming Load)
• Weather

Experimental Details

• Baselines: ARIMA\Prophet\LSTMa\LSTnet\DeepAR\Informer w\ canonical self-attention\Reformer\LogSparse
• Hyper-parameter tuning: grid search

5. Conclusion

[1]Tsai, Y.-H. H.; Bai, S.; Yamada, M.; Morency, L.-P.; and Salakhutdinov, R. 2019. Transformer Dissection: An Uni- fied Understanding for Transformer’s Attention via the Lens of Kernel. In ACL 2019, 4335–4344.
[2]Child, R.; Gray, S.; Radford, A.; and Sutskever, I. 2019. Generating Long Sequences with Sparse Transformers. arXiv:1904.10509.
[3]Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.-X.; and Yan, X. 2019. Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Fore- casting. arXiv:1907.00235.
[4]Beltagy, I.; Peters, M. E.; and Cohan, A. 2020. Longformer: The Long-Document Transformer. CoRR abs/2004.05150.