选第二大算法(锦标赛算法)

算法描述

算法：FINDSECOND

输入：n个数的数组a[0...n-1]

输出：数组中的第二大的数second

算法思路

在选最大选最小算法中，我们将数组中的数两两分组进行比较，然后在较大的一组中选出最大的，在较小的一组中选出最小的，时间复杂度T(n)=⌈3n/2⌉-2，对比我们直接在整个数组中先选出最大，再选出最小时间复杂度T(n)=2n-3，时间复杂度更低。选第二大同样的道理，如果我们直接先选最大，再选第二大，时间复杂度同样是T(n)=2n-3。

因此选第二大算法我们也可以有类似的思路，采用锦标赛的形式将数组中的数两两分组进行比较，获胜的元素进入下一轮的比较，并且在比较中记录下所有对应获胜元素所淘汰的元素，当冠军元素也就是最大值max产生时，max所对应的所有被max淘汰的元素也被记录了下来，并且第二大的数second也在其中，然后我们只需要在这些元素中找最大的数即为第二大的数second。

算法实现的数据结构，锦标赛的比较过程可以概括为一个满二叉树，元素个数如若不足满二叉树则需进行补充。我们需要了解在满二叉树中父节点序号与儿子节点序号之间的关系，当父节点序号为k时，左儿子节点序号为2k，右儿子节点序号为2k+1。

假设当前我们需要从有5个元素的数组a[1，8，22，15，3]中选出第二大的数，那么第一轮比较的过程可以描述为一个满二叉树，如下图所示：

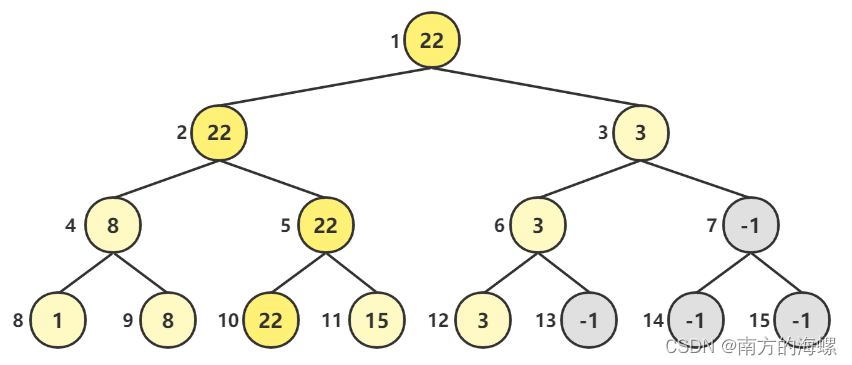
用一个数组b来存放这些数在数组a中的下标(注意此算法中所有的下标从1开始)，为空的地方就赋值为-1，然后通过左右子树不断的比较，将大数放到父亲节点，一直到根节点，得到下图数组b的结构：

 然后采用一个递归实现来进行第二次比较，递归地寻找到与最大数max比较的所有元素，然后从下往上覆盖最大数max，直到根节点就得到了第二大数second。

 

算法分析

常规算法先选出最大的数，再在剩余的数中选出最大的数就是原数组的第二大的数T(n)=n-1+n-2=2n-3。

而选第二大算法时间复杂度计算如下：

第一阶段分组比较选出最大值，所有元素总共比较了n-1次
第二阶段在被max淘汰的⌈logn⌉个元素中选取最大比较⌈logn⌉-1次
则T(n)=n-1+⌈logn⌉-1=n+⌈logn⌉-2

算法实现

using namespace std;
#include<iostream>

void pk(int* a, int* b, int bLen, int index, int max)
{
	int left = index * 2;
	int right = index * 2 + 1;

	//在满二叉树中迭代地寻找与最大数比较过的数

	//当找到存放最大数序号的叶子节点时将其改写为-1
	if (left > bLen || right > bLen)
	{
		b[index - 1] = -1;
		return;
	}

	//如果左儿子是最大数则继续递归左儿子，反之递归右儿子
	if (b[left - 1] == max)
	{
		pk(a, b, bLen, left, max);
	}
	else
	{
		pk(a, b, bLen, right, max);
	}

	if (a[b[left - 1] - 1] > a[b[right - 1] - 1])
	{
		b[index - 1] = b[left - 1];
	}
	else
	{
		b[index - 1] = b[right - 1];
	}
}

int findSecond(int a[], int n)
{
	int x = 1;
	while (x < n)
	{
		x = x << 1;
	}
	int* b = new int[2 * x - 1];

	//将b数组中后x个元素装入1到n的标号
	for (int i = 0; i < x; i++)
	{
		if (i < n)
		{
			b[x - 1 + i] = i+1;
		}
		else
		{
			b[x - 1 + i] = -1;
		}
	}

	for (int i = 2 * x - 2; i > 0; i-=2)
	{
		if (b[i] < 0)
		{
			if (b[i - 1] >= 0)
			{
				b[(i - 1) / 2] = b[i - 1];
			}
			else
			{
				b[(i - 1) / 2] = -1;
			}
		}
		else
		{
			if (a[b[i] - 1] > a[b[i - 1] - 1])
			{
				b[(i - 1) / 2] = b[i];
			}
			else
			{
				b[(i - 1) / 2] = b[i - 1];
			}
		}
	}

	pk(a, b, 2 * x - 1, 1, b[0]);

	int second = a[b[0] - 1];
	delete[]b;

	return second;
}

int main(void)
{
	int a[5] = { 1,8,22,15,3 };
	cout << findSecond(a, 5);
}

参考：

锦标赛(n个数中求第一和第二大的数)_有时间也搞搞算法！-优快云博客