C++-计算两个一维数组的卷积

最新推荐文章于 2024-09-30 15:06:45 发布

榴莲小怪兽

最新推荐文章于 2024-09-30 15:06:45 发布

阅读量2.9k

点赞数

CC 4.0 BY-SA版权

分类专栏： C++

原文链接：https://blog.youkuaiyun.com/HopesunIce/article/details/100576655

C++ 专栏收录该内容

9 篇文章

订阅专栏

本文深入探讨了卷积运算的基本原理，详细介绍了卷积后数组长度的计算方法，并提供了两种不同的C++实现方式，包括直接计算和使用数组下标判断的卷积算法，适合于信号处理和图像处理领域的初学者和技术人员。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

卷积后数组长度：m + n - 1
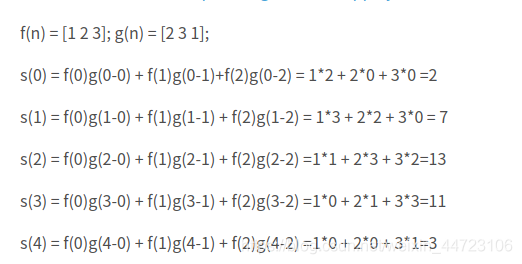
在这里插入图片描述
方法1（OK）

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <vector>
#include <queue>
#include <map>
#include <algorithm>
using namespace std;
#define INF 0xfffffff
#define maxn 100010

int main() {
    //int m = 5, n = 5;
    //int a[5] = {0, 1, 0, 2, 1}, b[5] = {0, 1, 0, 2, 1};
    int m = 3, n = 3;
    int a[5] = {1, 2, 3}, b[5] = {2, 3, 1};
    int i, j;
    int k = m + n - 1; //卷积后数组长度
    int c[k];
    memset(c, 0, sizeof(c)); //注意一定要清零
    /**卷积计算**/
    for(i = 0; i < k; i++) {
        for(j = max(0, i + 1 - n); j <= min(i, m - 1); j++) {
            c[i] += a[j] * b[i - j];
        }
        cout << c[i] << " ";
    }
    /****/
    cout << endl;
}

结果如下：
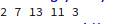
在这里插入图片描述

方法2

#include<iostream>
using namespace std;
int main()
{
	int Array1[] = { 1,2,3 }, Array2[] = { 2,3,1 };
	int temp;
	int n = sizeof(Array1) / sizeof(int) + sizeof(Array2) / sizeof(int) - 1;
	int Array3[sizeof(Array1) / sizeof(int) + sizeof(Array2) / sizeof(int) - 1] = {0,0,0,0,0};
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			//之所以加上这个判断 是因为在C和C++数组元素的下表不能是负数  
			//目前所知 只有在python中 数组元素可以为下标 a[-1]代表数组的倒数第一个元素  
			if (i - j < 0||i-j>2)
			{
				temp = 0;
			}
			else
			{
				temp = Array2[i - j];
			}
			Array3[i] = Array3[i] + Array1[j] * temp;
		}
	}
	for (int i = 0; i < n; i++)
	{
		cout << Array3[i] << endl;
	}
	return 0;
}