P4127同类分布（数位dp）

最新推荐文章于 2023-01-09 11:47:51 发布

原创最新推荐文章于 2023-01-09 11:47:51 发布 · 229 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

数位dp 专栏收录该内容

1 篇文章

订阅专栏

本文介绍如何使用数位DP（动态规划）算法，解决在指定区间内找到满足特定条件（如数位和能被原数整除）的数的数量问题。通过控制数位和枚举，有效降低空间复杂度，实现高效求解。

P4127同类分布（数位dp）

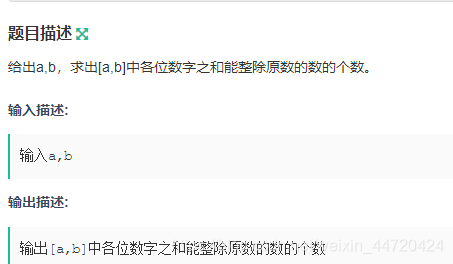
在这里插入图片描述
题目要求在某区间内满足一定条件的数的个数，选用数位dp，控制上届枚举。

题中涉及两个变量：原数，原数的数位和。

如果我们根据原数枚举，判断数位和能否整除原数，dp的一维需要1e18左右，占用空间较大，控制数位和枚举，最大位9*18=162，占用空间小很多，因此我们用控制数位和枚举。

代码如下：

# include <bits/stdc++.h>
using namespace std;
long long dp[20][200][200];
long long bit[20];
int mod;

long long dfs(int pos,int res,int sum,int lim)//当前位，当前位组合数的余数，当前数位和，该位是否受限
{
    if(pos==-1) return (res==0 && sum==mod?1:0);//枚举完成，且该数合法。res==0表示该数%mod为0，即为mod的倍数。sum==mod表示该数位和等于我们此次枚举的数位和。
    if( !lim && dp[pos][res][sum]!=-1) return dp[pos][res][sum];//不受限，且已经记忆化存储过，直接返回，无需重复计算
    int top=lim?bit[pos]:9;//枚举上限，若该位受限，控制上届枚举，则上届只能取到bit[pos]，如果不受限，可以取到9
    long long num=0;
    for(int i=0;i<=top;i++) //进行该位枚举
    {
        num+=dfs(pos-1,(res*10+i)%mod,sum+i,lim && top==i);
    }
    if(!lim) dp[pos][res][sum]=num;//不受限时，记忆化存储
    return num;
}

long long solve(long long x)//处理x
{
    int cnt=0;
    long long ans=0;
    while(x)//将每一位存储在bit[]数组中
    {
        bit[cnt++]=x%10;
        x/=10;
    }
    for(mod=1;mod<=9*cnt;mod++)//枚举数位和
    {
        memset(dp,-1,sizeof(dp));
        ans+=dfs(cnt-1,0,0,1);
    }
    return ans;
}

int main ()
{
    long long lx,rx;
    cin>>lx>>rx;
    cout<<solve(rx)-solve(lx-1)<<endl;
    return 0;
}