【剑指offer】二叉树专题

一、给定一个二叉树和其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的指针。

分析
法一：既然给了二叉树的某个结点，且二叉树存储着指向父结点的指针（next），那我们可以先找到根节点，再对树进行中序遍历，最后根据中序遍历结果找到给定结点的下一结点

法二：

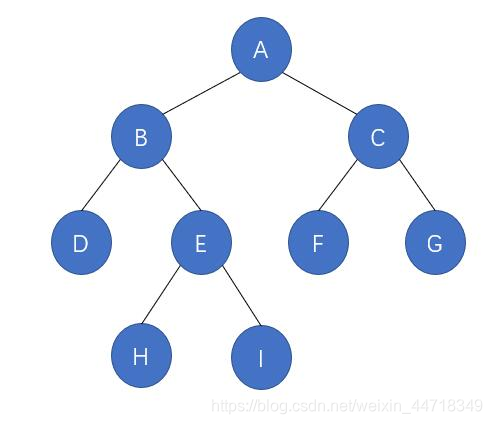
以该二叉树为例，中序遍历为：{D,B,H,E,I,A,F,C,G}

仔细观察，可以把中序下一结点归为几种类型：

有右子树，下一结点是右子树中的最左结点，例如 B，下一结点是 H

无右子树，且结点是该结点父结点的左子树，则下一结点是该结点的父结点，例如 H，下一结点是 E

无右子树，且结点是该结点父结点的右子树，则我们一直沿着父结点追朔，直到找到某个结点是其父结点的左子树，如果存在这样的结点，那么这个结点的父结点就是我们要找的下一结点。例如 I，下一结点是 A；例如 G，并没有符合情况的结点，所以 G 没有下一结点

法一的代码：

    List<TreeLinkNode> list = new LinkedList<>();
    public TreeLinkNode GetNext(TreeLinkNode pNode)
    {
        TreeLinkNode node = pNode;
        while (node.next!=null)
            node = node.next;
        inOrder(node);
        int i=0;
        for (TreeLinkNode resNode:list) {
            if(resNode==pNode)
                break;
            i++;
        }
        if(i<list.size()-1)
            return list.get(i+1);
        return null;

    }
    private void inOrder(TreeLinkNode node){
        if (node!=null){
            inOrder(node.left);
            list.add(node);
            inOrder(node.right);
        }
        return;
    }

二、镜面对称二叉树。请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。
分析：重点就在于递归传入的参数：

public class isSymmetrical {
    boolean isSymmetrical(TreeNode pRoot)
    {
        if (pRoot==null)
            return true;
        return dfs(pRoot.left,pRoot.right);

    }
    private boolean dfs(TreeNode node1,TreeNode node2){
        if(node1==null&&node2==null)
            return true;
        else if(node1!=null&&node2!=null){
            if(node1.val!=node2.val)
                return false;
            else {
                return dfs(node1.left,node2.right)&&dfs(node1.right,node2.left);
            }
        }
        else
            return false;
    }
}

三、按层级之字形打印二叉树
按层级的，总结出来都使用BFS配合队列

public class Print {
    private ArrayList<ArrayList<Integer>> res = new ArrayList<>();

    public ArrayList<ArrayList<Integer>> Print(TreeNode pRoot) {
        if(pRoot==null)
            return res;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(pRoot);
        int curr=0;
        while (!queue.isEmpty()){
            //每一个while就是一层
            ArrayList<Integer> list = new ArrayList<>();
            int size = queue.size();
            for(int i=0;i<size;i++){
                TreeNode node = queue.poll();
                if(node==null)
                    continue;
                list.add(node.val);
                queue.offer(node.left);
                queue.offer(node.right);
            }
            if(curr%2==1)
                Collections.reverse(list);
            if(list.size()>0)
                res.add(list);
            curr++;
        }

        return res;
    }

}

四、二叉树的序列化与反序列化

分析：使用前序遍历。好处是：反序列化的时候，由于采用的是先序遍历，此时如果遇到了#号，我们知道左边结束了,要开启右边，如果再次遇到#,表示当前整个部分的左边结束了要开始右子树，依次类推。

public class SerializeTree {

    private int index = 0;

    String Serialize(TreeNode root) {
        if(root==null)
            return "";
        return helperSerialize(root,new StringBuilder()).toString();
    }

    TreeNode Deserialize(String str) {
        //反序列化的时候，由于采用的是先序遍历，此时如果遇到了#号，我们知道左边结束了,要开启右边，
        // 如果再次遇到#,表示当前整个部分的左边结束了要开始右子树。。依次类推。
        if(str==null||str.length()==0)
            return null;
        String[] arr = str.split("!");
        return helperDeserialize(arr);
    }

    TreeNode helperDeserialize(String[] arr){
        if("#".equals(arr[index])){
            index++;
            return null;
        }
        TreeNode node = new TreeNode(Integer.valueOf(arr[index]));
        index++;
        node.left = helperDeserialize(arr);
        node.right = helperDeserialize(arr);
        return node;
    }

    StringBuilder helperSerialize(TreeNode root,StringBuilder sb){
        if(root!=null)
            sb.append(root.val+"!");
        else{
            sb.append("#!");
            return sb;
        }
        helperSerialize(root.left,sb);
        helperSerialize(root.right,sb);
        return sb;
    }
}

五、判断一个数组是不是二叉搜索树的后序遍历

解题思路：BST的后序序列的合法序列是，对于一个序列S，最后一个元素是x （也就是根），如果去掉最后一个元素的序列为T，那么T满足：T可以分成两段，前一段（左子树）小于x，后一段（右子树）大于x，且这两段（子树）都是合法的后序序列。完美的递归定义 。

    public boolean VerifySquenceOfBST(int [] sequence) {
        if(sequence==null||sequence.length==0)
            return false;
        if (sequence.length==1)
            return true;
        int root = sequence[sequence.length-1];
        List<Integer> left = new ArrayList<>();
        List<Integer> right = new ArrayList<>();

        int cut = -1;
        for(int i=0;i<sequence.length-1;i++){
            if(sequence[i]<root)
                left.add(sequence[i]);
            else {
                cut = i;
                break;
            }
        }

        if(cut>=0){
            for(int j=cut;j<sequence.length-1;j++){
                if(sequence[j]>root)
                    right.add(sequence[j]);
                else
                    return false;
            }
        }

        if(left.size()+right.size()==sequence.length-1){
            boolean leftFlag = true;
            boolean rightFlag = true;
            if(left.size()>0){
                if(!VerifySquenceOfBST(left.stream().mapToInt(i -> i).toArray()))
                    return false;
            }
            if(right.size()>0){
                if(!VerifySquenceOfBST(right.stream().mapToInt(i -> i).toArray()))
                    return false;
            }
        }
        else
            return false;

        return true;
    }

六、将二叉搜索树转换成一个排序的双向链表

解题思路：
1.将左子树构造成双链表，并返回链表头节点。
2.定位至左子树双链表最后一个节点。
3.如果左子树链表不为空的话，将当前root追加到左子树链表。
4.将右子树构造成双链表，并返回链表头节点。
5.如果右子树链表不为空的话，将该链表追加到root节点之后。
6.根据左子树链表是否为空确定返回的节点。

public class Convert {
    public TreeNode Convert(TreeNode pRootOfTree) {
        if(pRootOfTree==null)
            return null;
        if(pRootOfTree.left==null&&pRootOfTree.right==null)
            return pRootOfTree;
        // 1.将左子树构造成双链表，并返回链表头节点
        TreeNode left = Convert(pRootOfTree.left);
        TreeNode p = left;
        // 2.定位至左子树双链表最后一个节点
        while (p!=null&&p.right!=null){
            p = p.right;
        }
        // 3.如果左子树链表不为空的话，将当前root追加到左子树链表
        if(p!=null){
            p.right = pRootOfTree;
            pRootOfTree.left = p;
        }
        // 4.将右子树构造成双链表，并返回链表头节点
        TreeNode right = Convert(pRootOfTree.right);
        // 5.如果右子树链表不为空的话，将该链表追加到root节点之后
        if(right!=null){
            pRootOfTree.right = right;
            right.left = pRootOfTree;
        }
        //6.根据左子树链表是否为空确定返回的节点。
        return left==null?pRootOfTree:left;

    }
}