当看到有序数组,时间复杂度限定为logN时,便想到二分法。
一、leetcode4寻找两个有序数组的中位数
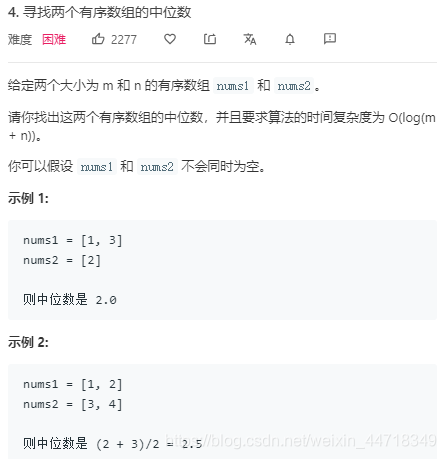
题目里要求了时间复杂度为logN,如果不做要求可以使用双指针分别指向两个数组的头部,一直移动到length之和的一半。
我们不妨用另一种思路,题目是求中位数,其实就是求第 k 小数的一种特殊情况,而求第 k 小数有一种算法。
假设我们要找第 7 小的数字。



7-7/2=4,4-4/2=2,2-2/2=1,------>7=4+2+1
即k-k/2一直递归下去,直到k=1时比较指针指向元素的大小。但是要处理一下极端情况:当一个数组的指针加k/2大于数组长度是取数组长度。
int i = Math.min(firstCurr+k/2-1,nums1.length-1);
int j = Math.min(secondCurr+k/2-1,nums2.length-1);
并且当一个数组的指针已经指向数组结尾时,返回另一数组的第k个元素:
if(firstCurr==nums1.length)
return nums2[secondCurr+k-1];
if(secondCurr==nums2.length)
return nums1[firstCurr+k-1];
整体代码:
/*
要求时间复杂度log,用二分,转换为求两个有序数组第k个小的数
*/
public class code4 {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
if((nums1==null||nums1.length==0)&&(nums2==null||nums2.length==0))
return 0.0;
int k1 = (nums1.length+nums2.length+1)/2;
int k2 = (nums1.length+nums2.length+2)/2;
//将偶数和奇数的情况合并,如果是奇数,会求两次同样的 k 。
int res1 = firstK(nums1, nums2, 0,0,k1);
int res2 = firstK(nums1, nums2, 0,0,k2);
return (res1+res2)/2.0;
}
private int firstK(int[] nums1, int[] nums2, int firstCurr,
int secondCurr, int k) {
if(firstCurr==nums1.length)
return nums2[secondCurr+k-1];
if(secondCurr==nums2.length)
return nums1[firstCurr+k-1];
if(k==1)
return Math.min(nums1[firstCurr],nums2[secondCurr]);
int i = Math.min(firstCurr+k/2-1,nums1.length-1);
int j = Math.min(secondCurr+k/2-1,nums2.length-1);
if(nums1[i]>=nums2[j])
return firstK(nums1, nums2, firstCurr,j+1,k-(j-secondCurr+1));
else
return firstK(nums1, nums2, i+1,secondCurr,k-(i-firstCurr+1));
}
}




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








