# 1.二维数据的卷积运算(对应图像的通道数为1时)
直接上图

最上方一行表示的是运算总过程,第一个框是输入数据,第二个框是滤波器(权重),它们之间是卷积运算符,第三个框是输出数据。
后面四行展示该例卷积运算的分步骤实现:间隔一行或一列,逐步应用滤波器(应用滤波器就是将输入数据的灰框部分与滤波器进行乘积累加运算),然后将计算结果输出到对应位置。
# 填充的概念
在进行卷积层的处理之前,有时要向输入数据的周围填入固定的数据(比如0等),这称为填充。如下图的例子,对大小为(4,4)的输入数据应用了幅度为1的填充。(即用幅度为1像素的0填充周围)

通过上述填充,输出数据的形状由原先的(2,2)变成了(4,4)。使用填充主要是为了调整输出大小,在保证空间大小不变的情况下,将数据传给下一层。(在反复进行多次卷积运算的深度网络中,若数据空间越变越小,那么在某个时刻输出大小就可能变为1,导致无法再运用卷积运算)
# 步幅的概念
应用滤波器的位置间隔称为步幅。之前的例子中步幅都是1,若将上述加了填充后的例子步幅设为3,则其运算过程如下图所示

从上图可以得出,增大步幅后,输出数据的空间变小了。
# 计算输出数据空间大小的公式
假设输入大小为(H,W),滤波器大小为(FH,FW),输出大小为(OH,OW),填充为P,步幅为S。可以得到如下计算式

# 2.三维数据的卷积运算(对应图像通道数大于1时)
# 输出数据的通道数为1时(只用一个滤波器)
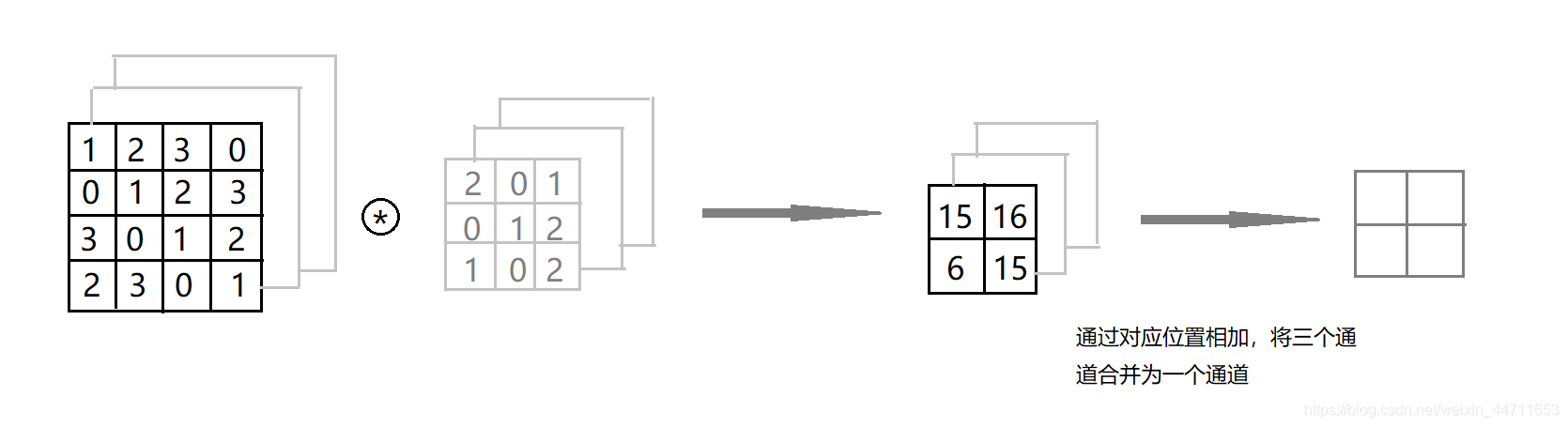
上图卷积运算的过程:首先每个通道独立地进行卷积运算,然后通过对应位置相加将多个通道合并为一个通道。(这里省略了添加偏置的步骤,加偏置的运算就是对上图现有结果进行同二维数据卷积运算加偏置同样的处理)
需要注意的是:1、输入数据和滤波器的通道数要设为相同的值。2、滤波器大小可以设置为任意值,但每个通道的滤波器大小要一致。
# 输出数据的通道数大于1时(运用多个滤波器)
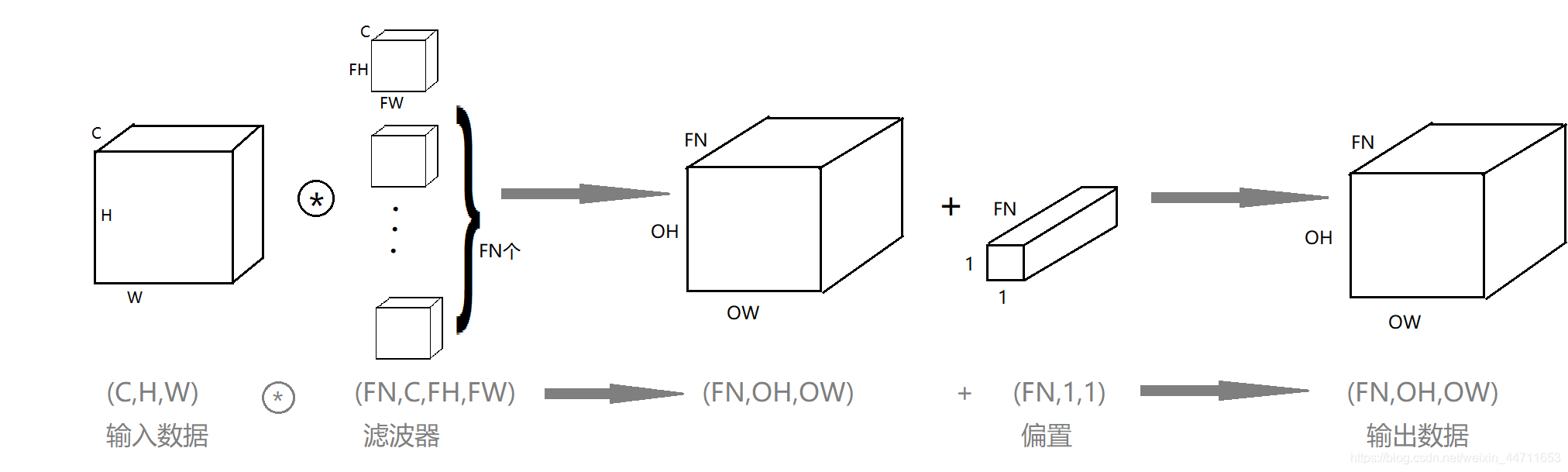
上图卷积运算的过程:首先对于每个滤波器进行一次上述所讲的(应用一个滤波器)的运算,由于共有FN个滤波器,所以生成的输出结果通道数为FN。然后对应每个通道加上一个偏置(这里每个通道加偏置的运算同二维卷积加偏置的运算),生成最终的输出数据。
注意这里输出数据对比输入数据的通道数已经发生了变化。
# 批处理的实现
批处理的结果和进行N次上述(输出数据通道数大于1时)处理的结果是相同的。但是由于批处理是一次性对大量数据进行运算,它会更高效和快速。为了实现批处理,传递的数据必须变成四维(批数目,通道数,高,宽)。

# 本博客参考了《深度学习入门——基于Python的理论与实现》(斋藤康毅著,陆宇杰译),特在此声明。





 本文详细解析了卷积神经网络中的关键概念,包括二维和三维数据的卷积运算,介绍了填充和步幅的作用,以及如何计算输出数据的空间大小。同时,文章还探讨了批处理的实现方法。
本文详细解析了卷积神经网络中的关键概念,包括二维和三维数据的卷积运算,介绍了填充和步幅的作用,以及如何计算输出数据的空间大小。同时,文章还探讨了批处理的实现方法。
















 529
529

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








