常见典型算法题解

一、动态规划

1、斐波那契数列

题

斐波那契数，通常用 F(n) 表示，形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给你 n ，请计算 F(n) 。

解

public class Solution {
    int fib(int N) {
        if(N==0){
            return 0;
        }
        if(N==1||N==2){
            return 1;
        }
        // 数组备忘录dp
        int[] dp = new int[N+1];
        dp[1] = dp[2] = 1;
        for (int i = 3; i <= N; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[N];
    }
}

2、凑零钱问题

题

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 ：

输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1

解

public class Solution {
    public int coinChange(int[] coins, int amount) {
        int max = amount + 1;
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, max);
        dp[0] = 0;
        for (int i = 1; i <= amount; i++) {
            for (int j = 0; j < coins.length; j++) {
                if (coins[j] <= i) {
                    dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
                }
            }
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }
}

二、回溯算法

1、全排列问题

题

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 ：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

解

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        List<Integer> output = new ArrayList<Integer>();
        for(int num : nums){
            output.add(num);
        }
        int len = nums.length;
        backtrack(len, output, res, 0);
        return res;
    }

        public void backtrack(int len, List<Integer> output, List<List<Integer>> res, int first) {
        // 所有数都填完了
        if (first == len) {
            res.add(new ArrayList<Integer>(output));
        }
        for (int i = first; i < len; i++) {
            // 动态维护数组
            Collections.swap(output, first, i);
            // 继续递归填下一个数
            backtrack(len, output, res, first + 1);
            // 撤销操作
            Collections.swap(output, first, i);
        }
    }

}

2、N皇后问题

题

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 ：

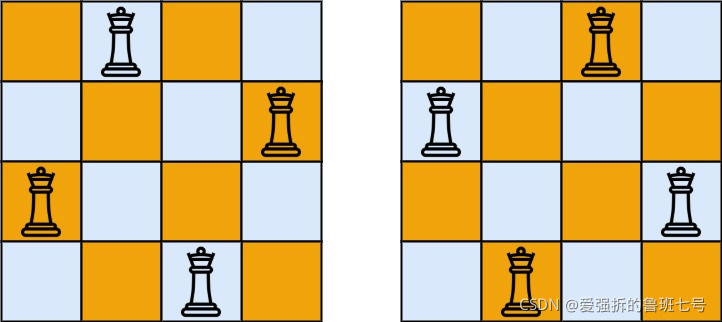
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

解

class Solution {
    public List<List<String>> solveNQueens(int n) {
        int[] queens = new int[n];
        Arrays.fill(queens, -1);
        List<List<String>> solutions = new ArrayList<List<String>>();
        solve(solutions, queens, n, 0, 0, 0, 0);
        return solutions;
    }

    public void solve(List<List<String>> solutions, int[] queens, int n, int row, int columns, int diagonals1, int diagonals2) {
        if (row == n) {
            List<String> board = generateBoard(queens, n);
            solutions.add(board);
        } else {
            int availablePositions = ((1 << n) - 1) & (~(columns | diagonals1 | diagonals2));
            wh