置信区间 VS 置信水平

经典统计学的核心思想是用样本估计总体，当样本足够大时，样本的均值方差等指标就会无限逼近整体的真实情况，且样本总是围绕在整体的平均值周围呈正态分布

置信区间即是用样本平均值估算总体平均值种方法。

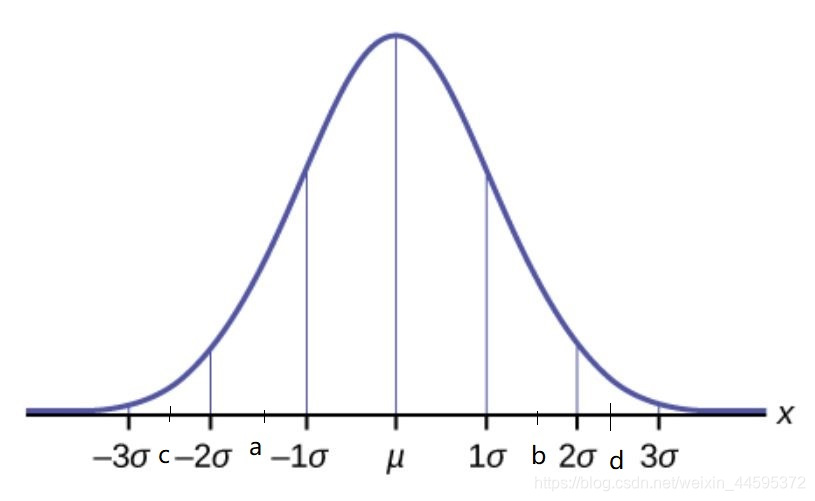
如上图：
x轴表示样本平均值
y轴表示样本平均值对应的概率
μ是总体的平均值
α是总体的方差
所有的样本平均值围绕在总体平均值两侧，并呈正态分布

置信区间描述的是:
我们估计的总体平均值与真实的总体平均值之间的误差
比如，真实的总体平均值是μ
我们经过多次样本试验，估计的总体平均值在[a,b]之间，[a,b]就是置信区间。

那么样本有多大概率会出现在[a,b]之间呢？
这就涉及到置信水平。
置信水平指：总体样本平均值出现在置信区间的概率

置信水平越高，说明样本范围越大，总体平均数出现在置信区间的概率就越大。
如上图：

总体平均值出现在[c,d]区间的概率比出现在[a,b]之间的概率大。

置信水平通常取95%，因为有95% 的样本平均值会落在[μ-2标准误差，μ+2标准误差]这个范围内

标准误差=样本标准差/开方(样本大小)

置信区间=[a,b]
a=样本本平均值-z标准误差
b=样本本平均值+z标准误差

推导过程见：
http://www.360doc.com/content/18/0317/16/15033922_737796626.shtml

z值可以从正太分布表中查到

根据置信水平m计算正太分布表中的z值:
（ps：正太分布表中的