关于浮点数丢失精度的原理

最新推荐文章于 2024-05-17 00:54:13 发布

原创最新推荐文章于 2024-05-17 00:54:13 发布 · 4.1k 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#float精度丢失 #double精度丢失 #浮点数精度丢失

Java基础专栏收录该内容

7 篇文章

订阅专栏

本文深入解析浮点数在计算机中的存储方式，揭示了浮点数精度丢失的原因，特别是针对0.1和0.2相加为何不等于0.3的谜题。文章详细解释了float和double类型如何依据IEEE754标准存储，并探讨了不同精度对数值表示的影响。

1、前言

首先我们必须要清楚

在计算机中所有的数值、代码、信息都是以01二进制存储的，也就是说我们输入的所有信息，最终都会表示成01二进制的形式。例如byte类型的 0000 1000表示的是整数8。

然后我们要清楚

所有的整数类型转换成二进制，看如下代码：

//表示11的二进制数计算
11 / 2 = 5 余 1   -->    1
5  / 2 = 2 余 1   -->  	 1
2  / 2 = 1 余 0   -->	 0	
1  / 2 = 0 余 1	  -->    1

所有的小数转换成二进制：看如下代码：

//0.1转换为二进制
0.1 * 2 = 0.2  -->0
0.2 * 2 = 0.4  -->0
0.4 * 2 = 0.8  -->0
0.8 * 6 = 1.6  -->1//然后去掉1
0.6 * 2 = 1.2  -->1
0.2 * 2 = 0.4  -->0

这个是一直循环下去的，所以呢计算机无法精确表示0.1，这个数值而是无限接近近似表示。
所以11的二进制数是1011，这样开来所有的整数最后都会被1 / 2 = 0这样结束。

2、我们先来看这样的一段代码

double dou = 234533464.456576564675d;
System.out.println("234533464.456576564675的运行结果："+dou);
float f = 997979759f;
System.out.println("997979759的运行结果："+f);
System.out.println("0.1+0.2的运行结果："+(0.2 +  0.1));

结果是：
在这里插入图片描述

惊奇不惊奇，刺激不刺激？这种采用浮点数的方法，输出的结果就是错误的。前两位后面的精度丢失，最后一个表示的不准确。
同样再看另外一段代码

float f1 = 20014999;  
double d1 = f1;  
double d2 = 20014999;  
System.out.println("f=" + f1);  
System.out.println("d=" + d1);  
System.out.println("d2=" + d2);

运行结果：
在这里插入图片描述

又是满满的疑问

double a = 0.3d;
System.out.println(0.2d+0.1d);
System.out.println(a);

在这里插入图片描述

我估计第三个直接刷新了好多人的三观，为啥直接存储就输出正确，运算就出错了呢？接下来我就围绕这几个问题对对大家一一解答。

3、我们先了解一下浮点数在计算机中是如何存储的。

float（32位浮点数）在计算机中的表示形式。

浮点数存储都遵守IEEE754标准，具体的运算应该在计算机组成原理中会重点介绍，标准如下：

其中S表示该浮点数的正负，E代表阶码，M代表的是尾数。
一个十进制数可以表示为 :
- 例如：20.59375在计算机中存储为：
- 20.59375 = 10100.10011，这里的s = 0，E = 4 + 127 = 131 ，M = 01001001；
- 所以存储格式为0100 001 1010 0100 1100 0000 0000 0000。这里就是存储在计算机中的数据。
- 至于为什么要加127，这个是IEEE754标准规定的，但是在维基百科以及其他文献中也并没有直接说为什么是这样。

double（64位浮点数）在计算机中的表示形式。

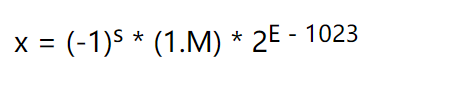
在这里插入图片描述

同理这个和上面的是一样的。

实际上这个1.M表示的是比如1000.111这个数，小数点移动位为1.000111，在754标准下存储为000111位数，这么做相当于是能够多保存一位，所以float可以保存的尾数是24位（23），double为53位而不是（52）。

4、我们首先来解决第二个问题

float f1 = 20014999;  
double d1 = f;  
double d2 = 20014999;

在这里插入图片描述

刚才不是说所有的整数都不会丢失精度吗，这个这么不一样呢。这个实际上也是因为float保留的位数太小造成的。
我们来分析一下：先输出他们的二进制位数

float f1 = 20014999;  
double d1 = f1;  
double d2 = 20014999;
long l1 = Float.floatToIntBits(f1);
long l2 = Double.doubleToLongBits(d1);
long l3 = Double.doubleToLongBits(d2);
System.out.println("f1=" + Long.toBinaryString(l1));  
System.out.println("d1=" + Long.toBinaryString(l2));  
System.out.println("d2=" + Long.toBinaryString(l3));

在这里插入图片描述

这里遵循IEEE754标准，但是注意这里面没有符号位，这三种结果为什么不同，我们这就分析，首先我告诉大家d2的输出结果是正确的。其中前11位是阶码1000 0010 111= 1047，后面的0011 0001 0110 0111 1001 0111 0000 0000 0000 0000 0000 0000 0000便是尾数，所以1047 - 1023 = 24，所以这个数真正的结果就是（别忘了1.M）：1.0011 0001 0110 0111 1001 0111然后小数点向右移动24位，就是10011 0001 0110 0111 1001 0111 = 20014999；

我们再来看第一个我们对比着尾数1.00110001011001111001100就会发现这里的尾数要比1.001100010110011110010111少了一位，而且少的一位是1，所以进行舍入处理，进行进位变成了1.00110001011001111001100。这样就产生了误差。也就变成了20015000。大家要清楚这里不光是尾数的位数少了还有相应的进位处理。同时要记得这里面float只能保存24位小数，double可以保留53位。

第二个就不用说了，由于本身f是错的，所以呢，赋值给d1之后仍然是是错的。
第三个由于54尾尾数可以放得下该数值的二进制数，所以是正确的。

到此为止呢，大家要明确一个概念就是，如果保存的浮点数超过了，该类型的最大精度，那么就会产生是很大很严重的问题，而且存入计算机中就会是存储的错的。明确这一点之后也就产生了我们第三个问题（非常奇怪的问题），所以呢我们最后来说这个问题。

5、解决第一个问题。

讲过第二个问题之后，第一个问题就非常好理解了，我们通过IEEE754的算法，可以得到这两个数的二进制表示形式，当用754标准去选取尾数的时候呢，就会截取掉一部分的尾数，造成精度丢失，其实原理是一样的。234533464.456576564675 = 2.34533464456576564675*e8,然后仍然是转换成754标准就失去了一些精度。具体的算法需要朋友们找相关的资料，这里不在赘述。

6、最奇怪的问题第三个问题。

double a = 0.1d;
double b = 0.2d;
double c = a + b;
System.out.println(a+"的二进制数:"+Long.toBinaryString(Double.doubleToLongBits(a)));
System.out.println(b+"的二进制数:"+Long.toBinaryString(Double.doubleToLongBits(b)));
System.out.println(c+"的二进制数:"+Long.toBinaryString(Double.doubleToLongBits(c)));
System.out.println(0.3+"                的二进制数:"+Long.toBinaryString(Double.doubleToLongBits(0.3d)));

在这里插入图片描述

大家可以看到直接存储的0.3和计算之后出现的（数学上来说的0.3）在计算机中保存的二进制编码是不同的，原因就在于首先计算机中无法精确表示0.1和0.2，所以实际上a，b并不是真正的0.1和0.2，已经出现了误差，所以相加之后计算出来的值就是错的，也就是0.30000000000000004。那至于为什么能够出现直接存储就可以正常显示呢，是由于编译器优化的结果，在不计算的情况下，可以正常显示，但是没有任何意义，因为一旦参与计算或者比较大小，那么这个值就不代表数学意义上的0.1了。