本文深入探讨了单调队列在算法问题中的应用，包括合并果子、滑动窗口、求区间最小值、切蛋糕和LargestRectangleinaHistogram等问题的解决策略，通过实例讲解和代码实现，帮助读者理解单调队列的高效性和灵活性。
学习资料
- 单调队列及其应用 By Codinginging
- 单调队列 By liukee
- 单调队列初步 By justmeh
- 单调栈&单调队列入门 By _tham
例题
合并果子
题目描述
在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。
每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过n-1次合并之后，就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。
假定每个果子重量都为1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。
例如有3种果子，数目依次为1，2，9。可以先将1、2堆合并，新堆数目为3，耗费体力为3。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为12，耗费体力为12。所以多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。
输入
输入包括两行，第一行是一个整数n(1<＝n<=10000)，表示果子的种类数。第二行包含n个整数，用空格分隔，第i个整数ai(1<＝ai<=20000)是第i种果子的数目。
输出
输出包括一行，这一行只包含一个整数，也就是最小的体力耗费值。输入数据保证这个值小于2^31。
输入输出样例
输入 #1 复制
3
1 2 9
输出 #1 复制
1
说明/提示
对于30％的数据，保证有n≤1000：
对于50％的数据，保证有n≤5000；
对于全部的数据，保证有n≤10000。
分析
见我的blog：luogu1090 合并果子
代码
/************************
User:Mandy.H.Y
Language:c++
Problem:luogu1090
Algorithm：
************************/
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e4 + 5;
int n,l1,r1,l2,r2;
long long ans;
long long q[maxn],a[maxn];
template<class T>inline void read(T &x){
x = 0;bool flag = 0;char ch = getchar();
while(!isdigit(ch)) flag |= ch == '-',ch = getchar();
while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar();
if(flag) x = -x;
}
template<class T>void putch(const T x){
if(x > 9) putch(x / 10);
putchar(x % 10 | 48);
}
template<class T>void put(const T x){
if(x < 0) putchar('-'),putch(-x);
else putch(x);
}
void file(){
freopen("testdata(1).in","r",stdin);
// freopen("1090.out","r",stdin);
}
void readdata(){
read(n);
for(int i = 1;i <= n; ++ i){
read(a[i]);
}
}
void work(){
l1 = 1,r1 = n + 1;
sort(a + 1,a + 1 + n);
l2 = r2 = 0;
for(int i = 1;i < n; ++ i){
long long x1,x2,x3,x4,x = 0;
if(l1 < r1) x1 = a[l1];
else x1 =1e15;
if(l1 < r1-1) x2 = a[l1 + 1];
else x2 = 1e15;
if(l2 < r2) x3 = q[l2];
else x3 =1e15;
if(x3 > x1){
x += x1;l1++;
if(x3 > x2) x+=x2,l1++;
else x += x3,l2++;
}else{
x += x3;l2++;
if(l2 < r2) x4 = q[l2];//这里l2已经++
else x4 = 1e15;
if(x4 < x1) x += x4,l2++;
else x += x1,l1++;
}
q[r2++] = x;
ans += x;
}
put(ans);
}
int main(){
// file();
readdata();
work();
return 0;
}
滑动窗口
luogu1886
题目描述
现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。
例如：
The array is [1 3 -1 -3 5 3 6 7], and k = 3.
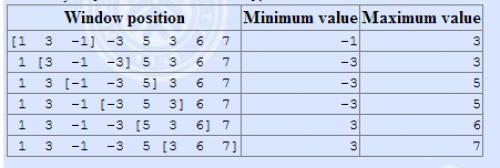
输入格式
输入一共有两行，第一行为n,k。
第二行为n个数(<INT_MAX).
输出格式
输出共两行，第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值
输入输出样例
输入 #1复制
8 3
1 3 -1 -3 5 3 6 7
输出 #1复制
-1 -3 -3 -3 3 3
3 3 5 5 6 7
说明/提示
50%的数据，n<=10^5
100%的数据，n<=10^6
分析
见我的blog：luogu 1886 滑动窗口
代码
//1886滑动窗口
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
int n,k,a[maxn],q[maxn],l,r;
void readdata()
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
}
void init()
{
freopen(".txt","r",stdin);
freopen(".txt","w",stdout);
}
void work()
{
l=r=0;
for(int i=1;i<=n;i++)
{
while(l<r && a[q[r-1]]>=a[i]) r--;
q[r++]=i;
while(l<r && q[l]<i-k+1) l++;
if(i>=k) printf("%d ",a[q[l]]);
}
printf("\n");
l=r=0;
for(int i=1;i<=n;i++)
{
while(l<r && a[q[r-1]]<=a[i]) r--;
q[r++]=i;
while(l<r && q[l]<i-k+1) l++;
if(i>=k) printf("%d ",a[q[l]]);
}
}
int main()
{
//init();
readdata();
work();
return 0;
}
求m区间内的最小值
题目描述
一个含有n项的数列(n<=2000000)，求出每一项前的m个数到它这个区间内的最小值。若前面的数不足m项则从第1个数开始，若前面没有数则输出0。
输入格式
第一行两个数n，m。
第二行，n个正整数，为所给定的数列。
输出格式
n行，第i行的一个数ai，为所求序列中第i个数前m个数的最小值。
输入输出样例
输入 #1复制
6 2
7 8 1 4 3 2
输出 #1复制
0
7
7
1
1
3
说明/提示
【数据规模】
m≤n≤2000000
ai≤3×10^7
分析
见我的blog：luogu 1440 求m区间内的最小值
代码
/**************************
User:Mandy.H.Y
Language:c++
Problem:luogu1440
Algorithm:
**************************/
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e6 + 5;
int n,l,r,m;
int q[maxn],a[maxn];
template<class T>inline void read(T &x){
x = 0;bool flag = 0;char ch = getchar();
while(!isdigit(ch)) flag |= ch == '-',ch = getchar();
while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar();
if(flag) x = -x;
}
template<class T>void putch(const T x){
if(x > 9) putch(x / 10);
putchar(x % 10 | 48);
}
template<class T>void put(const T x){
if(x < 0) putchar('-'),putch(-x);
else putch(x);
}
void file(){
freopen("1440.in","r",stdin);
freopen("1440.out","w",stdout);
}
void readdata(){
read(n);read(m);
}
void work(){
for(int i = 1;i <= n; ++ i){
read(a[i]);
while(l < r && i - q[l] > m) l++;
if(l >= r) puts("0");
else put(a[q[l]]),putchar('\n');
while(l < r && a[q[r - 1]] >= a[i]) r--;//>=
q[r++] = i;
}
}
int main(){
// file();
readdata();
work();
return 0;
}
切蛋糕
题目描述
今天是小Z的生日，同学们为他带来了一块蛋糕。这块蛋糕是一个长方体，被用不同色彩分成了N个相同的小块，每小块都有对应的幸运值。
小Z作为寿星，自然希望吃到的第一块蛋糕的幸运值总和最大，但小Z最多又只能吃M小块(M≤N)的蛋糕。
吃东西自然就不想思考了，于是小Z把这个任务扔给了学OI的你，请你帮他从这N小块中找出连续的k块蛋糕(k≤M)，使得其上的幸运值最大。
输入格式
输入文件cake.in的第一行是两个整数N,M。分别代表共有N小块蛋糕，小Z最多只能吃M小块。
第二行用空格隔开的N个整数，第i个整数Pi代表第i小块蛋糕的幸运值。
输出格式
输出文件cake.out只有一行，一个整数，为小Z能够得到的最大幸运值。
输入输出样例
输入 #1复制
5 2
1 2 3 4 5
输出 #1复制
9
输入 #2复制
6 3
1 -2 3 -4 5 -6
输出 #2复制
5
说明/提示
对20%的数据，N≤100。
对100%的数据，N≤500000，|Pi|≤500。 答案保证在2^31-1之内。
分析
见我的blog：luogu 1714 切蛋糕
代码
/**************************
User:Mandy.H.Y
Language:c++
Problem:luogu1440
Algorithm:
**************************/
#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e5 + 5;
int n,l,r,m;
long long ans = -1e15;
int q[maxn],a[maxn];
template<class T>inline void read(T &x){
x = 0;bool flag = 0;char ch = getchar();
while(!isdigit(ch)) flag |= ch == '-',ch = getchar();
while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar();
if(flag) x = -x;
}
template<class T>void putch(const T x){
if(x > 9) putch(x / 10);
putchar(x % 10 | 48);
}
template<class T>void put(const T x){
if(x < 0) putchar('-'),putch(-x);
else putch(x);
}
void file(){
freopen("1440.in","r",stdin);
freopen("1440.out","w",stdout);
}
void readdata(){
read(n);read(m);
}
void work(){
//前缀和
for(int i = 1; i <= n ; ++ i){
read(a[i]);a[i] += a[i - 1];
while(l < r && i - q[l] > m) l++;
//这里 i - q[l] > m，因为a[i] - a[j-1]才是j到i的区间和
// ans = max(ans,(long long)a[i]);不能要，a[i]是前缀和
ans = max(ans,(long long)a[i] - a[q[l]]);
while(l < r && a[q[r-1]] >= a[i]) r--;//>=
q[r++] = i;
}
put(ans);
}
int main(){
// file();
readdata();
work();
return 0;
}
Largest Rectangle in a Histogram
分析
题目翻译及题解：POJ 2559 Largest Rectangle in a Histogram
代码
/************************
User:Mandy.H.Y
Language:c++
Problem:POj 2559
Algorithm：
************************/
//#include<bits/stdc++.h>
#include<cstdio>
#include<iomanip>
#include<cmath>
using namespace std;
const int maxn = 1e5 + 5;
int n,l,r;
int q[maxn];
struct Node{
int h,l,r;
}node[maxn];
template<class T>inline void read(T &x){
x = 0;bool flag = 0;char ch = getchar();
while(!isdigit(ch)) flag |= ch == '-',ch = getchar();
while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar();
if(flag) x = -x;
}
template<class T>void putch(const T x){
if(x > 9) putch(x / 10);
putchar(x % 10 | 48);
}
template<class T>void put(const T x){
if(x < 0) putchar('-'),putch(-x);
else putch(x);
}
void file(){
freopen("2559.in","r",stdin);
// freopen("1090.out","r",stdin);
}
void work(){
read(n);
while(n){
long long ans = 0;
for(int i = 1;i <= n; ++ i) read(node[i].h),node[i].l = i,node[i].r = i;
//初始化l，r
l = r = 0;
for(int i = 1;i <= n; ++ i){
while(l < r && node[q[r - 1]].h >= node[i].h) node[i].l = node[q[r - 1]].l,r--;
//q中存的是编号，更新时 node[i].l = node[q[r - 1]].l，也可以是剩下的那个坐标 +1，但是要判空
q[r++] = i;
}
l = r = 0;
for(int i = n; i >= 1; -- i){
while(l < r && node[q[r - 1]].h >= node[i].h) node[i].r = node[q[r - 1]].r,r--;
q[r++] = i;
ans = max(ans,(long long)node[i].h * (node[i].r - node[i].l + 1));
}
put(ans);
putchar('\n');
read(n);
}
}
int main(){
// file();
work();
return 0;
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
