程序设计作业第4题-记忆化搜索+剪枝

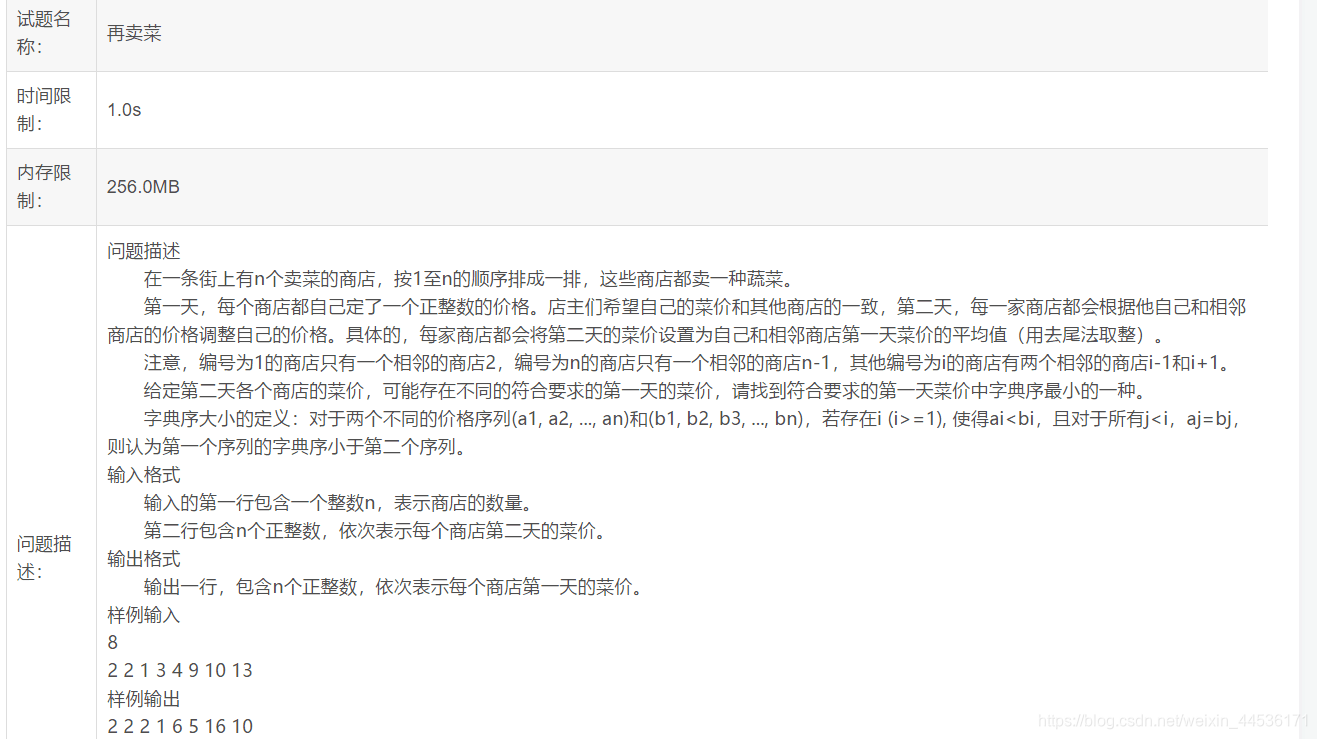
给定第二天菜价a[n]回推第一天菜价b[n]
则有递推公式(b[k-1]+b[k]+b[k+1])/3=a[k];
所以b[k+1] = 3 * a[k] - b[k] - b[k-1];
或者b[k+1] = 3 * a[k] - b[k] - b[k-1] + 1;
或者b[k+1] = 3 * a[k] - b[k] - b[k-1] + 2;
所以可以用b[k]和b[k-1]表示b[k+1]，枚举三种情况 用记忆化搜索 + 剪枝即可
最后一天的菜价需要特殊处理因为他只有一个邻近商家
第一天的菜价也只有两种可能,枚举并分别进行dfs即可
据说可以用差分约束，等我学会了再补差分约束的题解
我绝对不会咕咕咕的，嗯！
直接放代码

#include <iostream>
#include <cstdlib>
using namespace std;
#define ll long long
const int maxn = 500;
ll a[maxn],b[maxn];
int dp[maxn][maxn][maxn];   //记忆化搜索
int day;
void dfs(int n,int x,int y)  //第n天,b[n-1],b[n]
{
    if(dp[n][x][y]) return;
	dp[n][x][y] = 1;
	if(n==day-1)  //最后一天特殊处理
	{
		if((3*a[n]-x)/2==a[day]||(3*a[n]-x+1)/2==a[day]||(3*a[n]-x+2)/2==a[day])
		{
			for(int i=1;i<=n;i++)
			{
				cout<<b[i]<<" ";
			}
			for(int i=0;i<3;i++)
			{
				if((3*a[n]-x+i)/2==a[day])
				{
					cout<<3*a[n]-x-y+i<<endl;
					exit(0); 
				}
			}
		}
		return;
	}
	for(int i=0;i<3;i++)
	{
	    b[n+1] = 3*a[n]-x-y+i;
	    if(b[n+1]>=1)
	    {
	    	dfs(n+1,y,b[n+1]);
		}
	}	
}
int main()
{
	cin>>day;
	for(int i=1;i<=day;i++)
	{
		cin>>a[i];
	}
	for(int i=1;i<=2*a[1];i++)
	{
		b[1] = i; b[2] = 2*a[1]-i;
		dfs(2,i,b[2]);
		b[1] = i; b[2] = 2*a[1]-i+1;
		dfs(2,i,b[2]);
	}
	return 0; 
}